Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Модель специального преобразования информации в защищенных инфокоммуникационных системах
Аннотация:
Abstract:
| Авторы: Голод В.В. () - , Чернышов В.И. () - , Шулика В.Д. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 10263 |
Версия для печати Выпуск в формате PDF (1.30Мб) |
Несмотря на значительное разнообразие современных средств и построенных на их основе подсистем защиты информации в инфокоммуникационных системах, их неизменным общим свойством является некоторое специальное преобразование, выполняемое над защищаемой информацией при ее хранении и передаче. Задачей такого преобразования является, в первую очередь, обратимое устранение семантической (и, соответственно, прагматической) составляющей информации (здесь не рассматривается задача удаления информации или уничтожения собственно сигнала) [1,2]. Очевидный пример – криптографическое преобразование, результатом применения которого является последовательность унитарных кодов, не поддающаяся непосредственно (то есть в данном случае без применения методов криптоанализа) ни семантической, ни прагматической интерпретации. Другим примером может выступать стеганография – особый вариант распределения исходной последовательности в случайной или псевдослучайной последовательности существенно большей длины. В этом случае представляется обоснованным говорить не только о преобразовании, но даже о скрытии самой сигнальной составляющей информации. Противоположным вариантом специального преобразования информации может служить ее сжатие (архивация), при котором исходная последовательность трансформируется в последовательность существенно меньшей длины. При этом восстановление семантической и прагматической составляющих требует применения специального алгоритма разжатия (разархивирования), а сама преобразованная последовательность имеет близкое к равномерному распределение унитарных кодов. Специальное преобразование обладает следующими основными свойствами. Во-первых, это преобразование должно быть ограниченно обратимо (за исключением случая уничтожения информации). Под ограниченной обратимостью понимается тот факт, что эта обратимость возможна лишь при определенных условиях, а именно, при наличии некоторой дополнительной информации о параметрах этого преобразования (ключ шифра, алгоритм применения стеганографии или сжатия данных). Очевидно, что количество этой дополнительной информации должно быть существенно меньше длины исходной преобразуемой последовательности унитарных кодов. Во-вторых, результатом преобразования исходной последовательности унитарных кодов, должна являться новая последовательность, в которой семантика скрыта. На практике это означает, что результирующая последовательность независимо от исходной должна носить псевдослучайный характер следования унитарных кодов, а их распределение должно быть близко к равномерному. Иначе обратное преобразование в ряде случаев может быть успешно выполнено при отсутствии упомянутой выше дополнительной информации (простейший пример тому – энтропийный анализ последовательности с выявлением относительных частот появления отдельных унитарных кодов [2,3]).
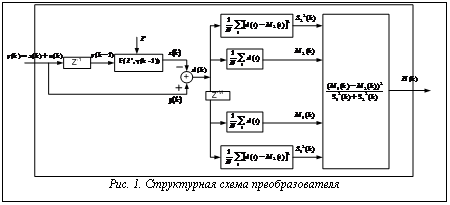
В частном случае криптографического преобразования информации (например, для алгоритмов потокового шифрования) такая ДС представляет генератор псевдослучайной последовательности байтов, накладываемой посредством гаммирования на передаваемую информационную последовательность. Задачей ДС является псевдохаотическое «размытие» исходной последовательности унитарных кодов в соответствии с некоторым заложенным детерминированным алгоритмом, существенно неустойчивым (в смысле устойчивости по Ляпунову [3], то есть небольшим различиям ключей и/или входной последовательности должны соответствовать существенные вариации выходной последовательности) как по ключу, так и по входным данным. Если предположить, что структура и свойства рассматриваемой ДС постоянны во времени, то отличие санкционированного обратного преобразования, выполняемого своими средствами защиты информации, от несанкционированного преобразования, выполняемого аналогичными системами противника, состоит в следующем. Первое преобразование выполняется в условиях наличия упомянутой выше дополнительной информации, то есть сведений о структуре и параметрах ДС, применяемом способе синхронизации и прочих параметрах, что позволяет синтезировать и применить обратное преобразование наиболее эффективно. Противник же лишен этой дополнительной информации или имеет неполную дополнительную информацию. Иными словами, противник, выполняя обратное преобразование, вынужден решать обратную задачу теории динамических систем при практически нулевой априорной информации, что, как известно [4,5], практически неразрешимо в сколько-нибудь общем виде. Полагая, что в качестве преобразователя выступает простейшая хаотическая ДС с дискретным временем, справедливо одномерное разностное уравнение вида х(k+1)=F[λ, x(k)], (1) где λ – параметр отображения; k=0,1,2,... – номер отсчета дискретного времени; F[λ,х(k)] – гладкая функция, отображающая некоторый отрезок оси x в себя и имеющая на этом отрезке единственный квадратичный экстремум. Пусть при передаче цифровой бинарной информации параметр λ(t) в (1) принимает два незначительно отличающихся значения λ1, λ2, каждое из которых соответствует хаотическому режиму ДС. Тогда, даже в отсутствие шума, различить в полученной после преобразования хаотической последовательности исходную последовательность не представляется возможным; статистические параметры преобразованной хаотической последовательности также остаются постоянными. Тем не менее при полностью известной дополнительной информации о виде и параметрах ДС, использованной для преобразования, можно получить исходную последовательность. Одна из возможных структур такого обратного преобразования может быть основана на использовании дискриминантной процедуры обработки преобразованных последовательностей и критерия Фишера (рис. 1). Идея этого критерия состоит в сравнении в каждый момент дискретного времени k на приемной стороне статистических характеристик соседних отрезков (окон) фиксированной длины N разности принятой хаотической последовательности y(k)=x(k)+n(k), (2) где n(k) – дискретный гауссовский белый шум, и пошагового прогноза сигнала х(k):
где d(k)=x(k)–y(k), (4) называемую линейной дискриминантной функцией, а также рассчитав средние значения разности смеси сигнала и шума у(k) и пошагового прогноза сигнала z(k) по (3) в окнах 1 и 2:
и соответствующие дисперсии
по достижении функцией
некоторого порога, можно судить о моментах времени скачкообразного изменения неизвестного параметра λ исходной последовательности.
Как и преобразователь, показанный на рисунке 1, следящий преобразователь (рис. 2) производит обработку мгновенной разности последовательностей у(k) и z(k). Последовательность z(k) есть результат вычисления нелинейной функции Дополнение первоначальной схемы обратного преобразователя (рис. 1) специальным блоком формирования оценки Δb с интервалом усреднения L0:
а также организация цепи отрицательной обратной связи с коэффициентом усиления R для коррекции рассогласования Δb позволяет снизить установившуюся ошибку слежения
где В соответствии с рассмотренной моделью обратное преобразование последовательности унитарных кодов осуществляется при наличии адекватной дополнительной информации. Работа обратного преобразователя противника в общем случае осуществляется в условиях полного отсутствия дополнительной информации о свойствах преобразователя средств защиты. В более простом частном случае, когда отсутствует лишь часть этой информации, под простейшей моделью обратного преобразователя противника можно понимать устройство, которое должно распознать сообщение a(t) при условии, что известны длительность тактового интервала L, моменты начала посылок (mL+1), вид ДС (1), генерирующей посылки При такой постановке задача построения оптимального преобразователя для противника сводится к задаче построения оптимального интерполятора на фиксированном интервале длительности L. Интерполятор позволяет найти оценку начального значения
то оптимальный интерполятор, обеспечивающий максимум апостериорной вероятности p(x(0)|{y(k)}), где {k}=1,...,L; F[x(k)]=F[l,x(k)] задана уравнением (1), {y(k)}=y(1),y(2),...,y(L) должен сначала выполнить операцию оптимальной фильтрации, то есть нахождения последовательности оценок {xf (k)}={хf(1), xf(2),.. хf(I)}, каждая из которых вычисляется на основе предшествующих значений {у(k)}, 1£k£L. Эта последовательность оценок запоминается. Затем оптимальный интерполятор, работающий в режиме «обратного времени», использует рекуррентный алгоритм определения оценки хs(0) начального значения x(0) по занесенным в память значениям {хf(L)}. Если х(k) является хаотической последовательностью, то применение указанной методики, как правило, оказывается неэффективным. Поэтому может быть предложен следующий эффективный алгоритм получения оценки хs(0). Поскольку уравнение ДС известно и известна оценка последнего значения хаотической последовательности xf(L), полученная оптимальной фильтрацией, то соответствующую ей оценку на предыдущем шаге можно получить с помощью обратной функции, то есть положив, что xs(L–l)=Finv[xf(L)] (11) и решив уравнение F[xs(L–1)]=xf(L) (12) относительно xs(L–1). Это уравнение в общем случае имеет несколько решений, и из них следует выбрать то, которое лежит ближе к оценке xf(L–1), полученной методом оптимальной фильтрации. Для нахождения xs(L–2) решается уравнение F[xs(L–2)]=xs(L–1) и выбирается значение xs(L–2), более близкое xf(L–2), и т.д. В рассматриваемом случае алгоритм имеет следующий вид. Уравнение
решается относительно xs(k) при каждом k в режиме обратного времени с начальным условием xs(L)=xf(L). Рассчитываются модули разностей двух решений уравнения (13). Выбор приемлемого решения осуществляется по правилу
При этом если одновременно с (13) рассматривать уравнение для точных значений сигнала F[x(k)]=x(k+1), (15) то можно получить равенство, связывающее дисперсии отклонений хS(k) и xS(k+l) от точных значений последовательности
где
Результаты оценки дисперсии предложенного алгоритма практически совпадают с теми, которые должны были получиться с помощью алгоритма оптимального сглаживания. С помощью описанного алгоритма производится восстановление каждой элементарной посылки с максимально достижимой точностью. Для восстановления сообщения a(t), передаваемого последовательностью посылок (12), входящей в сумму у(k), необходимо выбрать алгоритм различения этих посылок. Один из возможных алгоритмов основан на использовании первой восстановленной последовательности оценок элементарной посылки хS1(1),хS1(2),...,xS1(L) в качестве опорной в корреляторе, который для посылки хSm(1),хSm(2),..., xSm(L) рассчитывает коэффициент корреляции A1m по формуле
Эта величина в конце интервала времени (m+1)L сравнивается с порогом η. Решение принимается в соответствии с правилом
При этом на выходе обратного преобразователя восстанавливаются две дополнительные последовательности: одна соответствует a(t)=1, другая a(t)=0. При отсутствии дополнительной информации о вероятностях появления нулей и единиц в исходной последовательности унитарных кодов их вероятности принимаются одинаковыми. В этом случае целесообразно полагать η=0,5. Таким образом, специально преобразование, выполняемое средствами защиты инфокоммуникационной системы в целях защиты информации, может рассматриваться в модельном представлении как нелинейная ДС в режиме установившихся хаотических колебаний. При этом связь между степенью защищенности передаваемой информации в условиях частичной доступности дополнительной информации о таком преобразовании противнику связана со структурой и свойствами этой ДС и определяется на основе соотношений (11–19). Список литературы 1. Павлов В.А., Павлов Р.В., Толстых Н.Н. Обобщенная модель процесса функционирования автоматизированных систем в режиме информационного конфликта. // Информация и безопасность. – 1999. - №4. 2. Шеннон К. Математическая теория связи. – М.: ИЛ, 1963. 3. Корн Т., Корн Г. Справочник по математике. – М.: Наука, 1978. 4. Алексеев В.М., Якобсон М.В. Символьная динамика и гиперболические динамические системы. – М.: Мир, 1979. – 312с. 5. Matsumoto K., Tsuda I. Calculation of information flow rate from mutual information. – Journal Physics Applied, 1988, vol.21, pp. 1405-1414. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=443 |
Версия для печати Выпуск в формате PDF (1.30Мб) |
| Статья опубликована в выпуске журнала № 4 за 2006 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Унифицированный информационный интерфейс и его реализация в комплексной САПР
- Правовая охрана программного обеспечения с точки зрения международного сотрудничества стран-членов СЭВ
- Реализация теней с помощью библиотеки OpenGL
- Макроэкономическая балансовая модель для стран с элементами переходной экономики
- Электронный глоссарий
Назад, к списку статей



 На основании этих свойств модельное представление специального преобразования информации средствами защиты может быть представлено некоторой нелинейной динамической системой (ДС) в режиме установившихся хаотических колебаний. При этом степень защищенности информации напрямую связана с характеристиками этой ДС.
На основании этих свойств модельное представление специального преобразования информации средствами защиты может быть представлено некоторой нелинейной динамической системой (ДС) в режиме установившихся хаотических колебаний. При этом степень защищенности информации напрямую связана с характеристиками этой ДС. , (3)
, (3) – невозмущенная оценка параметра ДС приемника, соответствующая либо λ1, либо λ2. Вводя разность
– невозмущенная оценка параметра ДС приемника, соответствующая либо λ1, либо λ2. Вводя разность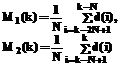 (5)
(5)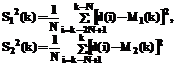 (6)
(6) (7)
(7)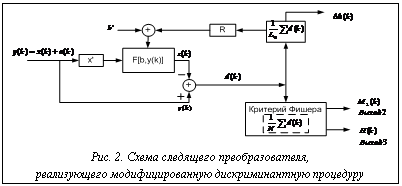 Пополнив схему (рис. 1) дополнительными блоками обработки мгновенных значений дискриминационной функции d(k), получим структурную схему модифицированного преобразователя с дискриминантной процедурой, которая, по сути, является следящим преобразователем (рис. 2).
Пополнив схему (рис. 1) дополнительными блоками обработки мгновенных значений дискриминационной функции d(k), получим структурную схему модифицированного преобразователя с дискриминантной процедурой, которая, по сути, является следящим преобразователем (рис. 2).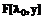 , вид которой идентичен виду функции
, вид которой идентичен виду функции  , используемой в исходном преобразователе, у которой отличается значение управляющего параметра
, используемой в исходном преобразователе, у которой отличается значение управляющего параметра  , (8)
, (8) , (9)
, (9)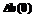 – начальное рассогласование.
– начальное рассогласование. и
и 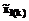 , и ее параметр l. Неизвестны лишь начальные условия
, и ее параметр l. Неизвестны лишь начальные условия  и
и  генерации посылок, соответствующих передаче символов "0" и "1".
генерации посылок, соответствующих передаче символов "0" и "1".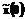 при k=0 по результатам наблюдения принимаемой последовательности у(k) при k=1,...,L. Если представить входную последовательность дешифратора на тактовом интервале передачи символа "0" (а(m)=0) уравнениями:
при k=0 по результатам наблюдения принимаемой последовательности у(k) при k=1,...,L. Если представить входную последовательность дешифратора на тактовом интервале передачи символа "0" (а(m)=0) уравнениями: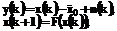 (10)
(10) (13)
(13)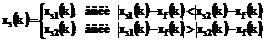 .(14)
.(14) , (16)
, (16)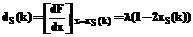 . (17)
. (17) . (18)
. (18) (19)
(19)