Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Модель несанкционированного доступа к информации в динамически изменяемых условиях
Аннотация:
Abstract:
| Авторы: Голод В.В. () - , Борисов М.А. () - , Трофимов В.В. () - , Осадчий А.И. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 8835 |
Версия для печати Выпуск в формате PDF (1.18Мб) |
При создании и эксплуатации автоматизированных телекоммуникационных систем связи и управления (АТКССУ) полнота обоснований требований и практических мероприятий по защите информации (ЗИ) от несанкционированного доступа (НСД) во многом определяется корректностью применяемых математических моделей и разработанных на их основе методик оценки возможностей нарушителя. Существующие модели НСД [1,2] базируются, как правило, на вероятностном описании динамики процессов добывания информации нарушителем в стационарных внешних условиях. Использование данных моделей для обоснования требований и практических мероприятий по ЗИ в АТКССУ приводит к существенным погрешностям в оценке реальных возможностей нарушителя, проявляющихся либо в занижении возможностей нарушителя, либо в неоправданном завышении организационно-технических требований по ЗИ (и, как следствие, существенном завышении затрат на их реализацию). Учет нестационарных изменений внешних условий применительно к задаче оценки возможностей средств объективного контроля реализован в [3], однако разработанная модель не охватывает наиболее часто встречающийся на практике факт, когда случайные моменты изменения внешних условий являются взаимонезависимыми, что существенно ограничивает возможность ее применения. Целью данной статьи является разработка модели оценивания возможностей нарушителя, учитывающей нестационарный характер динамического изменения взаимонезависимых внешних условий, существенным образом влияющих на эффективность действий нарушителя. Несанкционированный доступ к обрабатываемой в АТКССУ (или в ее элементах) информации в рассматриваемой модели представляется следующим образом. В течение интервала времени [0..T] нарушитель осуществляет попытки НСД к информации, обрабатываемой в АТКССУ. В случайный момент времени
где В практике разработки математических моделей вид ПРВ реальных процессов точно не известен, поэтому они аппроксимируются табличными ПРВ. В [4] показано, что наиболее точным и универсальным аппроксимирующим распределением реальных процессов с ограниченным последействием является обобщенное распределение Эрланга вида k(1), в котором один параметр равен l1, а остальные (k-1) параметров равны l0. Плотность распределения вероятности и функция распределения Эрланга k(1) вычисляются по формулам:
Для аппроксимации реальной случайной величины распределением Эрланга k(1) его параметры вычисляются по следующим формулам [4]:
где Рассмотрим порядок построения модели на примере трех случайных моментов изменения внешних условий SO – начальное состояние процесса (НСД не осуществлен); SD – конечное состояние процесса (НСД нарушителем осуществлен); Si, Sij, Sijk (i, j. k=1..3, j¹i, k¹j) – состояния, соответствующие последовательному наступлению i-го, j-го и k-го моментов изменения внешних условий. Вероятностно-временные характеристики (ВВХ) перехода процесса по состояниям динамического графа описываются следующими условными переходными ПРВ:
Переходные ПРВ динамического графа, помеченные звездочкой, являются условными в смысле операции конфликтного обусловлива- ния, применяемой в теории динамического кон- фликта [5], поэтому они определяются по следующим выражениям:
где i, j, k – обобщенные индексы (номера) случайных моментов динамического изменения внешних условий с учетом последовательности их появления: i, j, k Ì 1..3, j¹i, k¹j; Исходными данными для рассматриваемой модели являются ПРВ НСД к информации в различных условиях
где Плотность распределения вероятности
где Аналитическое решение исходной системы интегро-дифференциальных уравнений (6) для выбранного аппроксимирующего распределения (1)-(3) является чрезвычайно сложной задачей. Применение методов численного решения интегро-дифференциальных уравнений или методов имитационного моделирования приводит к необходимости разработки алгоритмически сложных автоматизированных расчетных и имитационных задач и, как следствие, к неприемлемой трудоемкости проведения расчетов. Для приведения системы (6) к аналитически вычисляемому виду целесообразно использовать разработанный в [3] метод, основанный на последовательной замене сложных конфликтно-обусловленных ПРВ эквивалентными им безусловными ПРВ. После применения данного метода выражения (4) примут следующий вид:
где С учетом выражений (7), ПРВ НСД нарушителем к информации в динамически изменяющихся внешних условиях, входящая в систему (6), примет следующий вид:
где a – введенные для краткости записи обобщенные индексы, принимающие следующие значения:
Выражение для вычисления выходного показателя модели (5) примет вид, аналогичный (7), с той лишь разницей, что вместо эквивалентных нормированных ПРВ Таким образом, в статье разработана новая модель оценивания возможностей НСД к информации, обрабатываемой в АТКССУ в динамически изменяющихся внешних условиях при допущении о взаимонезависимом и случайном характере моментов изменения условий. Использование данной модели позволяет более точно и корректно описать динамику добывания информации нарушителем в реальных ситуациях их применения и за счет этого повысить качество решения задач ЗИ в АТКССУ. Опыт использования данной модели показал, что для большинства случаев достаточно рассмотренных в статье трех случайных моментов изменения внешних условий. Вместе с тем расширение данной модели на большее количество учитываемых изменений внешних условий не связано с трудностями принципиального характера. Список литературы 1. Седякин Н.М. Элементы теории случайных импульсных потоков. – М.: Сов. радио, 1965. - 260 с. 2. Максимов Ю.Н. и др. Технические методы и средства защиты информации. - СПб.: ООО «Издательство Полигон», 2000. - 320 с. 3. Иванов С.М., Язов Ю.К. Расчет распределения времени выявления сигналов средствами объективного контроля в изменяющихся внешних условиях. //Радиотехника. - 1996. - №6. - С. 69-73. 4. Тараканов К.В., Овчаров А.А., Тырышкин А.Н. Аналитические методы исследования систем. – М.: Сов. радио, 1974. - 240 с. 5. Дружинин В.В., Конторов Д.С., Конторов М.Д. Введение в теорию конфликта. – М.: Радио и связь, 1989. - 288 с. 6. Тихонов В.И., Миронов М.А. Марковские процессы. – М.: Сов. радио, 1977. - 488 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=492 |
Версия для печати Выпуск в формате PDF (1.18Мб) |
| Статья опубликована в выпуске журнала № 4 за 2005 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Оценка защищенности информации от несанкционированного доступа при помощи имитационной модели системы защиты информации
- Оптимизация обработки информационных запросов в СУБД
- Эволюционная модель формирования структур виртуальных предприятий
- Формирование программ развития больших систем административно-организационного управления
- Использование графических постпроцессоров VVG и LEONARDO в вычислительной гидродинамике
Назад, к списку статей



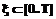 происходит изменение внешних условий, поэтому на интервалах
происходит изменение внешних условий, поэтому на интервалах 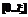 и
и 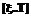 вероятностно-временные характеристики (ВВХ) доступа нарушителя к информации в АТКССУ различны. Если нарушитель не смог осуществить НСД на интервале
вероятностно-временные характеристики (ВВХ) доступа нарушителя к информации в АТКССУ различны. Если нарушитель не смог осуществить НСД на интервале 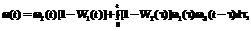
 ,
, 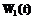 – ПРВ и функция распределения (ФР) появления случайной точки
– ПРВ и функция распределения (ФР) появления случайной точки 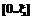 (момента смены внешних условий) на интервале [0..T];
(момента смены внешних условий) на интервале [0..T];  ,
, 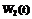 – ПРВ и ФР осуществления НСД нарушителем на интервале
– ПРВ и ФР осуществления НСД нарушителем на интервале  (до смены внешних условий);
(до смены внешних условий); 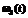 – ПРВ осуществления НСД нарушителем на интервале
– ПРВ осуществления НСД нарушителем на интервале 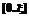 (после изменения внешних условий).
(после изменения внешних условий).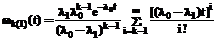 , (1)
, (1)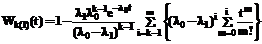 . (2)
. (2)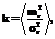
 (3)
(3)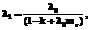
 ,
,  – математическое ожидание и дисперсия реального распределения, которое аппроксимируется распределением Эрланга k(1);
– математическое ожидание и дисперсия реального распределения, которое аппроксимируется распределением Эрланга k(1);  – операция округления в сторону наибольшего целого.
– операция округления в сторону наибольшего целого.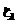 ,
, 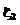 ,
, 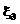 . При взаимной независимости размещения на отрезке времени [0..T] точек
. При взаимной независимости размещения на отрезке времени [0..T] точек 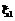 ,
,  и
и 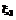 динамический граф процесса НСД нарушителя к информации, хранящейся (обрабатываемой) в АТКССУ, содержит следующие состояния:
динамический граф процесса НСД нарушителя к информации, хранящейся (обрабатываемой) в АТКССУ, содержит следующие состояния: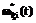 ,
,  – ПРВ наступления первого изменения внешних условий (одного из трех) до осуществления НСД и ПРВ осуществления НСД нарушителем до первого изменения внешних условий соответственно;
– ПРВ наступления первого изменения внешних условий (одного из трех) до осуществления НСД и ПРВ осуществления НСД нарушителем до первого изменения внешних условий соответственно; ,
, 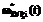 , где i, j Ì 1..3, j¹i – ПРВ наступления второго изменения внешних условий (одного из двух оставшихся) до НСД и ПРВ осуществления НСД нарушителем до второго изменения внешних условий соответственно;
, где i, j Ì 1..3, j¹i – ПРВ наступления второго изменения внешних условий (одного из двух оставшихся) до НСД и ПРВ осуществления НСД нарушителем до второго изменения внешних условий соответственно;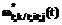 ,
,  , где i, j, k Ì 1..3, j¹i, k¹j – ПРВ наступления третьего изменения внешних условий до НСД и ПРВ НСД нарушителя до третьего изменения внешних условий соответственно;
, где i, j, k Ì 1..3, j¹i, k¹j – ПРВ наступления третьего изменения внешних условий до НСД и ПРВ НСД нарушителя до третьего изменения внешних условий соответственно;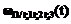 – ПРВ НСД нарушителя к информации, хранящейся (обрабатываемой) в АТКССУ, после того как произошли все три изменения внешних условий (последовательность их наступления в данном случае значения не имеет).
– ПРВ НСД нарушителя к информации, хранящейся (обрабатываемой) в АТКССУ, после того как произошли все три изменения внешних условий (последовательность их наступления в данном случае значения не имеет).
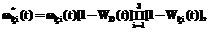
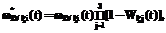 (4)
(4)
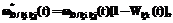
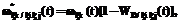
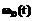 ,
,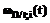 ,
, – ПРВ НСД нарушителя к информации без изменения внешних условий, при первом изменении внешних условий, а также при первом и втором изменении внешних условий;
– ПРВ НСД нарушителя к информации без изменения внешних условий, при первом изменении внешних условий, а также при первом и втором изменении внешних условий; 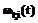 ,
,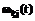 ,
, – ПРВ наступления каждого из трех моментов изменения внешних условий.
– ПРВ наступления каждого из трех моментов изменения внешних условий. ,
, 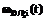 ,
,  ,
,  , которая определяется по методам, изложенным в [1], кроме того, исходными данными являются ПРВ наступления каждого из трех моментов изменения внешних условий. Выходным показателем модели является вероятность НСД к информации, обрабатываемой в АТКССУ нарушителем за заданное время t, определяемое по следующему выражению:
, которая определяется по методам, изложенным в [1], кроме того, исходными данными являются ПРВ наступления каждого из трех моментов изменения внешних условий. Выходным показателем модели является вероятность НСД к информации, обрабатываемой в АТКССУ нарушителем за заданное время t, определяемое по следующему выражению: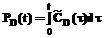 , (5)
, (5)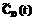 – ПРВ прихода процесса НСД к информации в конечное состояние SD в момент времени t.
– ПРВ прихода процесса НСД к информации в конечное состояние SD в момент времени t.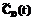 определяется в соответствии с теорией полумарковских процессов [6] по следующей системе интегро-дифференциальных уравнений:
определяется в соответствии с теорией полумарковских процессов [6] по следующей системе интегро-дифференциальных уравнений: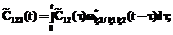
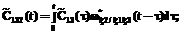
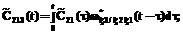
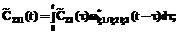
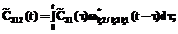
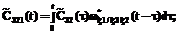
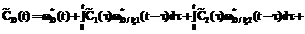
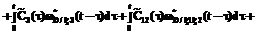

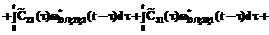
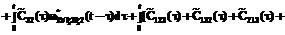
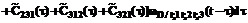 ,
,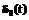 – дельта-функция в точке t=0.
– дельта-функция в точке t=0.
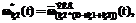
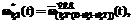

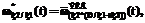
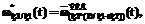
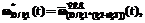
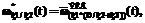
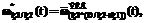
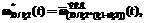 (7)
(7)
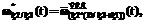
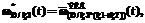
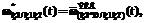

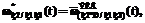

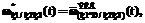

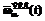 – нормированная эквивалентная ПРВ (a – обобщенный индекс); знаки «+» и «*» в индексах определяют вид использованных для получения данной эквивалентной ПРВ типовых подстановок, а скобки в индексах отражают последовательность применения типовых подстановок [3].
– нормированная эквивалентная ПРВ (a – обобщенный индекс); знаки «+» и «*» в индексах определяют вид использованных для получения данной эквивалентной ПРВ типовых подстановок, а скобки в индексах отражают последовательность применения типовых подстановок [3].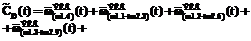
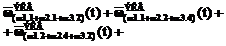
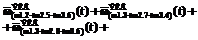 (8)
(8)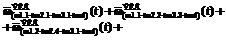

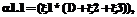
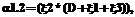
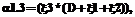
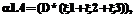
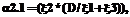
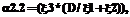
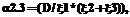

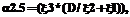
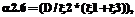
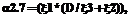

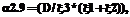


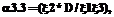

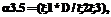
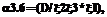
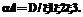
 необходимо использовать соответствующие эквивалентные нормированные функции распределения
необходимо использовать соответствующие эквивалентные нормированные функции распределения 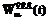 , вычисляемые по выражению (2).
, вычисляемые по выражению (2).