Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Влияющие воздействия и погрешности измерений в метрологическом моделировании контроля неэлектрических параметров
Аннотация:
Abstract:
| Автор: Карпов В.М. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 11073 |
Версия для печати Выпуск в формате PDF (1.41Мб) |
Создание программного продукта для метрологического моделирования рассматривается как средство, обеспечивающее возможность достижения требуемой точности при измерении неэлектрических величин параметрическими преобразователями в информационно-измерительных каналах (ИИК) гибких производственных систем (ГПС). Показано, что без понимания задач обеспечения точности нельзя создать модель, адекватную реальному ИИК системы контроля и диагностики, и обеспечить прогнозирование метрологических характеристик. Развитие автоматических систем управления, совершенствование систем контроля измерений и диагностики (КИД) в современных компьютеризированных производствах неразрывно связаны с разработкой программного продукта для анализа метрологических свойств ИИК, преобразующих неэлектрические величины в электрические параметры и, в конечном счете, в сигналы. Создание таких информационно-измерительных систем могло бы способствовать успеху автоматизации производства. Отсутствие необходимых инструментальных средств, преобразующих с требуемой точностью неэлектрические параметры объектов и средств производства в электрические сигналы в реальных условиях протекания технологических процессов – это факт конца двадцатого века. Решенные в этой области задачи пока носят фрагментарный характер. Недостаточный объем объективной информации о состоянии технологических процессов и средств производства является самым большим тормозом в создании систем управления разного уровня и безлюдного производства в целом. Системы контроля и диагностики в автоматизированном компьютеризированном промышленном производстве, если их сравнивать с измерительно-информационными системами безлюдного управления в других областях, например в ракетной технике, будут нуждаться в десятках и сотнях тысяч измерительных каналов, информирующих производственную систему об ее состоянии в режиме реального времени. Задачи создания и эксплуатации системы КИД, обеспечения ее точности могут решаться только на основе широкого внедрения моделирующих технологий и нового программно-математического обеспечения. Режимы работы ИИК с параметрическим преобразователем Система реального ИИК всегда настолько сложна, что мы пока не в состоянии ее полностью понять и описать. При моделировании неизбежно исключается часть реальных характеристик изучаемой системы или объекта. От того, насколько хорошо и достоверно мы представляем реальную ситуацию, будет зависеть и результат моделирования. Моделирование, во многом оставаясь интуитивным, всегда требует познания физической сущности объектов и процессов, протекающих в окружающей среде и в контролируемых технологических процессах. Подобно всем мощным средствам, метрологическое моделирование способно дать либо очень хорошие, либо очень плохие результаты, в зависимости от правильности представления имитируемых объектов. Преобразование измеряемой неэлектрической величины (НВ) в электрический параметр описывается функцией преобразования параметра (ФПП) Это же преобразование в пределах диапазона измерения представляется статической ФПП (СФПП). В основе решения проблемы создания ИИК должно лежать правильное описание ФПП преобразователя, включенного в параметрическую измерительную цепь (ПИЦ). Если этот этап завершен успешно, то можно приступить к созданию электрической измерительной цепи, обеспечивающей наилучшие (приемлемые) метрологические характеристики ИИК в целом при наличии влияющих воздействий (ВВ). Если под ВВ подразумевать всю совокупность ВВ на все элементы ИИК, то задача неразрешима. В ИИК, предназначенных для технологических систем автоматизированного производства, есть одна существенная особенность. Здесь в погрешности доминируют составляющие, обусловленные ВВ на датчик, то есть на устройство с первичным преобразователем, находящееся либо непосредственно в зоне выполнения технологического процесса, либо расположенное на технологическом оборудовании. Будем считать, что в ИИК все ВВ сосредоточены на датчике непосредственно, поскольку вторичные преобразователи всегда могут быть вынесены в стойку технологического оборудования, находящуюся в нормальных условиях и защищенную от сильных ВВ, обусловленных протеканием технологического процесса или работой оборудования. СФПП является фундаментальной метрологической характеристикой измерительного устройства и во многом определяет возможности достижения требуемых метрологических характеристик для ИИК в целом. Если ФПП определена, то, следовательно, определен и импеданс контура преобразователя как функция измеряемой величины Z(H). Пусть Поскольку от глубины модуляции параметра (его вариации под влиянием входных воздействий на преобразователь) зависит весь ход и во многом успех создания ИИК, то режим работы преобразователя будем характеризовать с помощью относительных изменений импеданса. Выделим два режима работы: РГМ – режим глубокой модуляции; РММ – режим малой модуляции. В процессе измерений модуляция импеданса контура преобразователя происходит как под действием измеряемой величины, так и ВВ одновременно. Вводя обозначения разнонаправленными стрелками рядом с каждой переменной, будем различать вклад каждой составляющей входной величины: если стрелка направлена вниз, то На диаграмме (рис. 1), пунктиром выделена область параметрической нестабильности. Работа в режимах, соответствующих этой области, всегда требует особой изобретательности в решении задачи обеспечения высокой точности измерений. Вместе с тем создание датчика, обеспечивающего работу в режиме 1 и 4-3, может быть достигнуто только благодаря большому опыту, интуиции и хорошей конструкторско-технологической подготовке специалиста. Во многих задачах таких режимов может просто не существовать. Тогда мы вынуждены вести творческий поиск, используя физически осуществимые режимы в области параметрической нестабильности. Воздействия на ПИЦ Поскольку входные воздействия определены как совокупность воздействий измеряемой величины и влияющих (мешающих) факторов, то любые воздействия на ИИК, исключая измеряемую величину, следует относить к ВВ. Именно этими воздействиями порождается погрешность ИИК. Отсюда вывод: при анализе точности ИИК следует исходить из оценки ВВ как по его природе, так и по его величине. Решение этой задачи всегда представляет собой трудности, а иногда и неразрешимые проблемы. Важно усвоить наличие одного обстоятельства – решение задачи о точности (о достоверности информации в системе управления) всегда надо начинать с анализа ВВ. В ГПС это становится неразрешимой проблемой, если не познаны процессы, лежащие в основе реальных технологий производственной деятельности автоматизируемого предприятия. Все ВВ можно разделить на аддитивные, не приводящие к изменению амплитуды сигнала несущей частоты генератора, но изменяющие выходной сигнал на преобразователе, и на модулирующие, изменяющие амплитуду сигнала генератора.
Сигнальные ВВ могут возникать как вследствие изменения параметров электрических цепей самого генератора или в результате нестабильности источников питания генератора, так и в результате появления наводок (помех) в проводах и кабелях, ведущих к ПП. Нестабильность генератора привела бы к появлению модулирующей составляющей на выходе, а наводки обусловят только появление аддитивной составляющей, не изменяя модуляцию на несущей частоте. Как правило, при выборе частоты генератора необходимо учитывать ожидаемые уровни и частотный диапазон электромагнитных наводок, чтобы эффективно решать задачу отстройки ИИК от аддитивной составляющей с помощью правильной фильтрации сигнала. Например, при работе с вихретоковыми или высокочастотными емкостными датчиками эта задача не вызывает больших трудностей. Если имеют место ВВ, изменяющие импеданс преобразователя или контура его электрической цепи, то сигнал на выходе будет модулироваться, то есть будет происходить вариация амплитуды по несущей частоте генератора. Аналогично воздействует на импеданс преобразователя и измеряемая величина, поэтому задача отстройки от влияющих воздействий в этом случае многократно усложняется. Если в предыдущем варианте частотный диапазон ВВ и сигнала генератора можно разнести на порядки, то, как правило, частотные диапазоны для измеряемой величины и для ВВ перекрывают друг друга или находятся в непосредственной близости. Отстройка с помощью фильтров становится невозможной или малоэффективной. Решение задачи повышения точности требует отыскания других путей. Проявление ВВ Случайная величина (в теории вероятностей) – это величина, принимающая в зависимости от случайного исхода испытания те или иные значения с определенными вероятностями. Случайная переменная, принимающая конечную или бесконечную последовательность различных значений, задается указанием этих значений и соответствующих им вероятностей. Таким образом, каждому значению случайной переменной противопоставляется, в отличие от простой переменной, значение вероятности ее появления: Вывод 1. Случайная величина может быть определена только на основе многократных испытаний, устанавливающих закон ее распределения. Это математическая сторона дела. Что касается физического или технического эксперимента, то здесь следует особо подчеркнуть, что вероятностные и другие закономерности, характеризующие случайную величину, должны быть установлены при неизменных условиях проведения эксперимента. Так, число очков, выпадающее на верхней грани игральной кости, представляет собой случайную величину, принимающую значения 1, 2, 3, 4, 5, 6 с вероятностью 1/6 каждое. Представим себе, что изменили условие эксперимента. К одной грани прикрепили парашют! Каким станет результат? Вывод 2. К случайным величинам (переменным) правомерно прибегать только в тех случаях, когда неизменность условий эксперимента подтверждена. Применимость теории явно становится функцией априорных знаний о системе, с которой имеет дело экспериментатор. Весьма часто это порождает очень серьезные трудности при корректном использовании теории математической статистики в решении конкретных инженерных задач. Применимость теории должна подтверждаться на основе априорных сведений об условиях работы системы и о проявлении влияющих воздействий в ней. Все сказанное прежде всего относится к информационной системе, поскольку анализ метрологических свойств этой системы базируется на использовании разностей высоких порядков, описывающих такие метрологические характеристики, как чувствительность и ее изменение, точность и ее изменение при вариации ВВ и т.д. Поскольку технический эксперимент, как и физический, всегда ограничен по количеству опытов, то на базе теории вероятностей возникла теория математической статистики. Математическая статистика решает задачи определения какого-то свойства множества (генеральной совокупности), полученного при неизменных условиях на основании познания этого свойства в подмножестве, образованном при тех же условиях, то есть принадлежащего этой генеральной совокупности. В математической статистике оценка стандартного отклонения (уклонения) определяется иной формулой, чем в теории вероятностей. Коррекция введена Бесселем в соответствии со здравым смыслом прагматичного экспериментатора. При отказе от многократных экспериментов мы выходим из поля вероятностных (статистических) оценок. Рассеяние становится бесконечным, то есть оценка некорректна. Подводя итог, скажем, что математическими методами течение случайных явлений может быть описано количественно, только если они наблюдались многократно и при неизменных условиях, а оценить рассеяние при однократном испытании невозможно. Сделать акцент на этом чрезвычайно важно, поскольку в информационной системе, обслуживающей систему управления технологическим оборудованием в режиме реального времени, изменения условий опыта могут произойти мгновенно, и эти временные интервалы вполне соизмеримы с постоянной времени ИИК. В условиях ГПС имеем дело с измерениями в режиме реального времени. ВВ могут изменяться сколь угодно быстро, поэтому результат каждого измерения не следует рассматривать как случайную величину. Решение задачи повышения точности измерений за счет статистических методов обработки результатов в силу непрерывно изменяющихся условий опыта становится некорректным. Величину, обладающую свойством принимать любое значение в заданном (предписанном) диапазоне, но не многократно, будем называть неопределенной. Немногократность заключается в том, что измерение физической величины может быть повторено, но при этом варьируются условия эксперимента. Стабильность условий измерения не обеспечивается и не гарантируется. Неопределенные ВВ могут иметь детерминированную связь с параметрами преобразователя или выходного сигнала. Воздействие влияющей величины, которое описывается детерминированной функцией детерминированного по своей природе, но неопределенного по величине аргумента, будет называться псевдосистематическим ВВ. Например, зависимость сопротивления тензопреобразователя, установленного на державке резца, от температуры известна (функция определена), но аргумент (температура) – величина неопределенная в данном опыте и может принимать любые значения в пределах, скажем, 20–100о С. Погрешности при таких ВВ будем относить к псевдосистематическим составляющим. Воздействие влияющей величины, неизвестной по своей природе, но приводящей к изменению параметра преобразователя в пределах заданного (предписанного) интервала, будет называться псевдодетерминированным ВВ. Например, сопротивление тензопреобразователя, установленного на державке резца, может принимать любые значения в пределах, скажем, 1%. Может измениться затяжка болтов, температура поверхности державки или изменятся свойства подложки преобразователя и т.д. В измерительном канале информация по этим параметрам не использована. Таким образом, физическая природа ВВ не определена, но результат предписан. Погрешности измерений и обработка результатов Разработка программного продукта для метрологического моделирования ИИК потребовала формулировки подходов к реализации рациональных путей в оценке погрешностей и точностных характеристик имитируемых объектов. Результат измерения – это значение физической величины, найденное путем ее измерения. Точность измерений – это качество измерений, отражающее близость результатов к истинному значению. Отклонение результата от истинного значения измеряемой величины называется погрешностью измерения. Поскольку истинное значение – это абстракция, к которой прибегают только для введения понятия погрешности измерения, то определенную таким образом погрешность назовем истинной. Истинное значение измеряемой физической величины никогда не известно. Для вычисления погрешности прибегают к отысканию величины, максимально приближенной к ее истинному значению. Это достигается использованием средств измерения высокой точности, что позволяет получить так называемое действительное значение искомой величины. Если Задача определения истинного значения и в фундаментальных, и в прикладных науках может иметь различный подход в ее решении. В инженерной практике истинной величине параметра предписывается значение, указанное в технической документации. В этом случае проблема отыскания истинного значения находит весьма тривиальное разрешение, поскольку погрешность исчисляется от номинальной величины контролируемого параметра – Таким образом, исчисление погрешности всегда требует взвешенного подхода в выборе величины, замещающей абстракцию в виде истинного значения, например, в задаче о статистическом контроле, очевидно, следует прибегать к использованию оценки математического ожидания Переходя к обобщению формулы вычисления погрешности, запишем В причинах неточности измерений кроется принципиальная невозможность достижения истинного значения измеряемой величины: - на средство измерения всегда действуют другие влияющие величины (окружающая среда), и средство измерения само влияет на объект контроля; - истинное значение – это абстракция. Существует только его приближение, описываемое в рамках логической модели с определенными допущениями (например, "диаметр" вала, выходное напряжение и т.д.). С целью обеспечения повышения точности измерений и снижения трудоемкости процессов контроля и измерений выделяют погрешности по различным признакам. Классификации позволяют проще понять суть процессов возникновения и формирования погрешностей. Усвоив эти знания, можно активно влиять на устранение или, по крайней мере, на уменьшение отдельных составляющих результирующей погрешности измерения. Классификация погрешностей по проявлению является одной из фундаментальных. При метрологическом моделировании ИИК для производственных систем выделение неопределенных ВВ логично приводит к классификации, показанной на диаграмме (рис. 2). Систематическая погрешность – это постоянная или закономерно изменяющаяся составляющая при измерении одной и той же величины многократно (математическое ожидание, среднее значение погрешности). Выделяют прогрессирующие (возрастающие или убывающие), периодические, изменяющиеся по сложному закону. Систематическая составляющая является результатом воздействия факторов, которые проявляют себя в каждом опыте, одинаково или закономерно изменяясь.
Исключение систематических погрешностей во многом определяется квалификацией экспериментатора, его знаниями существа процессов, конкретных условий проведения измерений, особенностей используемых ИИК и методов. Если такая составляющая погрешности обнаружена и определена предварительно с помощью средств более высокой точности, то возможно введение поправок и повышение точности. Введение случайных составляющих погрешностей представляет собой удачную попытку использования формального математического приема для ухода от реальной причинно-следственной связи между влияющими воздействиями и погрешностью измерения. В диаграмме классификации погрешностей (рис. 2) заключена, по сути, и классификация ВВ, и этим подчеркивается причинная связь между ВВ и ошибками измерения. Как известно, случайная погрешность – это составляющая, изменяющаяся при повторных измерениях одной и той же величины случайным образом. В отличие от систематической, случайная составляющая погрешности легко обнаруживается по разбросу данных даже при работе с неизменными средствами измерений. Для случайной погрешности предполагается, что при повторении актов измерения статистические характеристики погрешности не изменяются. При этом возникает трудность, состоящая в том, что реально нет возможности ни измерять одну и ту же величину (она не постоянна в абсолютном понимании), ни осуществлять измерения в одних и тех же условиях. Обладает ли погрешность статистической устойчивостью? При оценке погрешности статистическими методами всегда необходимо принимать во внимание то обстоятельство, что математическими методами течение случайных явлений может быть описано количественно, только если они наблюдались многократно и при неизменных условиях опыта. Решение задачи повышения точности измерений за счет статистических методов обработки результатов в силу непрерывно изменяющихся условий опыта становится некорректным или физически нереализуемым. Величину, обладающую свойством принимать любое значение в заданном (предписанном) диапазоне, но не многократно, мы определили ранее как величину неопределенную. Погрешность, обусловленную воздействием неопределенной влияющей величины, которое описывается детерминированной функцией детерминированного по своей природе, но неопределенного по величине аргумента, будем называться псевдосистематической. Погрешность, обусловленную воздействием неопределенной влияющей величины, неизвестной по своей природе, но приводящей к изменению параметра преобразователя в пределах заданного (предписанного) интервала, будет называться псевдодетерминированной. Грубые погрешности – это результат воздействия факторов, полностью неопределенных и не подчиняющихся вероятностным законам, или факторов имеющих устойчивые характеристики, но погрешности по своему значению существенно превышают ожидаемые погрешности, описываемые статистическими методами. Отметим, что классификации и их признаки являются весьма условными и не всегда, например, можно четко выделить инструментальные и методические погрешности и т.д., однако польза от использования классификаций в практической работе несомненна. Вычисление погрешности в задачах метрологического моделирования Рассмотрим ИИК с позиций решения задачи о точности измерений неэлектрической величины электрическими методами. На вход ИИК воздействует измеряемая величина и вектор ВВ. Блок ИИК характеризуется параметрами, функционально зависимыми от влияющих величин. Пусть V – сигнал при наличии ВВ и H=const, а V0 – сигнал при том же значении измеряемой величины, но в отсутствие ВВ. Тогда, по определению, погрешность сигнала V на выходе ИИК при наличии ВВ и при значении измеряемой величины H=const будет вычисляться по формуле Если статическую функцию преобразования (СФП) представить в соответствии со структурой измерительного устройства (ИУ), где P –параметры ИУ, подвергаемые ВВ, то текущее значение выходного сигнала может быть представлено в виде При отсутствии ВВ Pi =P0;V=V0 и При наличии ВВ параметр изменяется в окрестностях рабочей точки Выходной сигнал может быть представлен в виде ряда Тейлора:
Сомножитель Под знаками сумм должны стоять члены ряда, описанные частными производными от первого до высоких порядков. Чем сильнее ВВ, тем большего порядка производные должны быть учтены при оценке погрешности:
При слабых ВВ, когда ΔPi< Тогда погрешность можно представить в виде следующего соотношения:
Как видим, рассматриваемый путь вычисления погрешности с помощью ряда Тейлора требует знания производных. При метрологическом моделировании, имея описание СФП, частные производные должны определяться ее многократным дифференцированием. Задача определения большого количества производных не только трудоемка, но и вряд ли оправдана, поскольку точнее и проще определить погрешность непосредственным вычитанием двух значений исходных функций V и V0, чем прибегать к их многократному численному дифференцированию и, в конечном итоге, к отбрасыванию остаточных членов бесконечного ряда. Значит, в метрологическом моделировании использовать разложение СФП в ряд Тейлора для вычисления погрешности нецелесообразно. Также нецелесообразно для вычисления погрешности использовать понятие дифференциала как главной линейной части приращения функции. Особенно это касается определения погрешности при сильных ВВ. При метрологическом моделировании погрешность следует вычислять как разность функций при наличии и отсутствии ВВ, то есть
Таким образом, задача корректного определения модели, описывающей СФПП в целом СФП ИИК, становится особенно актуальной при разработке программного продукта метрологического моделирования. Список литературы 1. Карпов В.М. Обратная задача метода наименьших квадратов при метрологическом моделировании. // Тр. VII науч-технич. конф.: Состояние и проблемы технических измерений. - М., 2000. 2. Карпов В.М. Симметрирование как средство обеспечения точности измерительных каналов, предназначенных для условий автоматизированного производства. // Проектирование и технология электронных средств. - 2001. - № 4. 3. Карпов В.М. Метрологическое моделирование информационно-измерительных каналов для контроля неэлектрических параметров // Проектирование и технология электронных средств. - 2002. - №1. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=505 |
Версия для печати Выпуск в формате PDF (1.41Мб) |
| Статья опубликована в выпуске журнала № 2 за 2006 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Правовая охрана программного обеспечения с точки зрения международного сотрудничества стран-членов СЭВ
- О выборе числа процессоров в многопроцессорной вычислительной системе
- Система поддержки принятия решений по планированию профессиональной структуры подготовки специалистов
- Структурно-параметрическая идентификация функций занятости и прогнозирование спроса на молодых специалистов
- Средства обеспечения надежности функционирования информационных систем
Назад, к списку статей



 – относительное изменение импеданса под действием измеряемой величины в интервале диапазона измерения. Совокупность эффекта изменения импеданса датчика под действием измеряемой величины и ВВ представляет собой входное воздействие.
– относительное изменение импеданса под действием измеряемой величины в интервале диапазона измерения. Совокупность эффекта изменения импеданса датчика под действием измеряемой величины и ВВ представляет собой входное воздействие.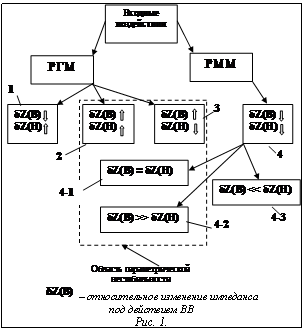 Модулирующие и аддитивные ВВ по-разному влияют на сигнал ПИЦ. Следовательно, должны существовать различные подходы к подавлению этих влияющих воздействий на выходной сигнал ИИК в целом.
Модулирующие и аддитивные ВВ по-разному влияют на сигнал ПИЦ. Следовательно, должны существовать различные подходы к подавлению этих влияющих воздействий на выходной сигнал ИИК в целом.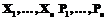 .
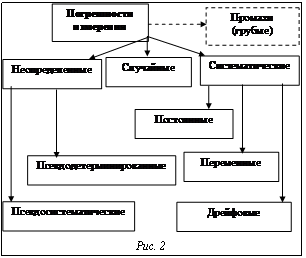
.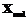 – действительное значение, то теперь формула для расчета абсолютной погрешности будет выглядеть так:
– действительное значение, то теперь формула для расчета абсолютной погрешности будет выглядеть так: 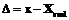 .
.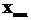 , заданной чертежом или другим документом:
, заданной чертежом или другим документом: 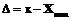 .
.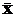 . Тогда погрешность (уклонение) определится формулой
. Тогда погрешность (уклонение) определится формулой 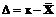 .
.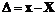 .
. Систематические составляющие погрешностей представляют наибольшие трудности в их обнаружении, ибо их наличие обнаруживается измерением параметра в тех же условиях, но с использованием других измерительных средств и методов.
Систематические составляющие погрешностей представляют наибольшие трудности в их обнаружении, ибо их наличие обнаруживается измерением параметра в тех же условиях, но с использованием других измерительных средств и методов.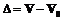 .
.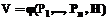
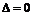 .
.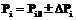 .
.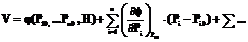 .
.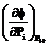 представляет собой коэффициент влияния (абсолютный).
представляет собой коэффициент влияния (абсолютный).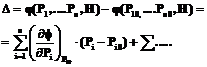
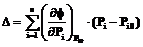 .
.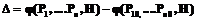 .
.