Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Интеграция прикладных систем на основе баз знаний
Аннотация:
Abstract:
| Автор: Евгенев Г.Б. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 11038 |
Версия для печати Выпуск в формате PDF (0.95Мб) |
Любой программный комплекс можно представить как триаду PC = , где PC – программный комплекс; F – функциональные компоненты, осуществляющие обработку данных; D – базы данных; C – управляющий программный комплекс. Графически такая декомпозиция представлена на рисунке 1. Для проведения функционального анализа прикладных областей и разработки функциональных моделей имеется международный стандарт IDEF0. На рисунке 1 функциональная схема интегрированного комплекса представлена в нотации этого стандарта. В этом комплексе функциональными компонентами F являются исполняемые модули прикладных систем в совокупности со служебными модулями, необходимыми для обеспечения совместной работы объединяемых систем.
Одним из наилучших формализмов моделирования управляющих комплексов являются сети Петри. С их помощью могут быть промоделированы многие системы, в особенности системы с независимыми компонентами, как, например, программное обеспечение. В этой связи в качестве средства для моделирования управляющего программного комплекса C целесообразно использовать сети Петри (см. рис.1). Для создания управляющих программных комплексов интегрированных прикладных систем непрограммирующими пользователями должны быть использованы средства экспертного программирования [1]. С использованием этих средств необходимо разработать методику описания управляющих комплексов в форме сетей Петри. Простое представление системы сетью Петри основано на двух основополагающих понятиях: событиях и условиях [2]. События – это действия, имеющие место в системе. Возникновением событий управляет состояние системы, которое может быть описано множеством условий. Условия – это предикат, или логическое описание состояния системы. Условие может принимать либо значение «истина», либо значение «ложь». Так как события являются действиями, то они могут происходить при выполнении соответствующих условий. Эти условия называют пред- условиями события. Возникающие действия могут изменить состояние системы и привести к выполнению других условий – постусловий.
Таблица
Описанное представление системы легко моделируется сетью Петри. В сети Петри условия моделируются позициями, а события – переходами. При этом входы перехода являются предусловиями соответствующего события, а выходы – постусловиями. Возникновение события равносильно запуску перехода. Выполнение условия представляется фишкой в позиции, соответствующей этому условию. Запуск перехода удаляет разрешающие фишки, представляющие выполнение предусловий и образует новые фишки, которые представляют выполнение постусловий. В теории сетей Петри вводятся понятия примитивных и непримитивных событий [2]. Примитивные события изображаются планками, а непримитивные – прямоугольниками. Определение этих двух классов событий имеет двоякое содержание: временное и структурное. Согласно первому подходу примитивным является мгновенное событие, а непримитивным – событие, длительность которого отлична от нуля. Второй подход используется при моделировании сложных систем на нескольких иерархических уровнях. При этом непримитивное событие представляет в качестве отдельного элемента целую подсеть. В дальнейшем будет использоваться именно такая трактовка непримитивных событий. Выполнение сети Петри, моделирующее поведение системы, рассматривается как последовательность дискретных событий. Порядок появления событий является одним из возможных, допускаемых основной структурой сети. Это может привести к недетерминированности в выполнении сети Петри. Если в какой-то момент времени разрешено более одного перехода, любой из нескольких возможных может стать «следующим» запускаемым. Это необходимо учитывать при разработке модели.
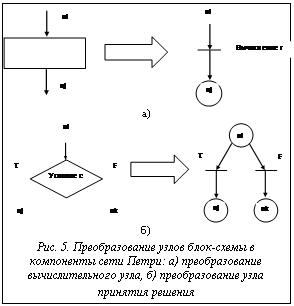
Вырожденным случаем параллельной системы обработки данных является система с одним процессом. Отдельный процесс описывается программой. Программа представляет два различных аспекта процесса: вычисление и управление. Вычисление связано с арифметическими и логическими операциями, вводом и выводом данных и т.п. Управление же связано не с вычислениями, а только с порядком их выполнения. Сети Петри удачно представляют струк- туру управления программ. Они предназначе- ны для моделирования упорядочения событий и потока информации, а не для выполнения вы- числений. Стандартный способ представления структуры управления программ – это блок-схемы, которые представляют поток управления в программе. Блок-схемы предназначаются не для указания конкретных вычислений, а для определения структуры программ. Основными компонентами блок-схем являются узлы двух типов: прямоугольники, представляющие вычислительные блоки, и ромбы, изображающие управляющие блоки (рис. 5). Эти блоки связываются между собой дугами. При переводе блок-схемы в сеть Петри узлы блок-схемы заменяют переходами, а дуги блок-схемы – позициями. Каждая дуга блок-схемы соответствует точно одной позиции сети Петри. Узлы блок-схемы представляются по-разному, в зависимости от типа узла: вычисления или принятия решения (рис. 5). При описании сетей Петри с помощью средств экспертного программирования переходы представляются с помощью модулей знаний, а позиции с помощью целочисленных переменных, указывающих наличие и количество фишек в переходе. Предусловия переходов преобразуются в пред- условия модулей знаний. Изменение состояний предусловий и постусловий осуществляется с помощью механизмов модулей знаний.
На рисунке 7 приведены модули знаний, соответствующие блоку принятия решения (рис. 5б).
При использовании экспертного программирования особый случай представляют сети Петри с обратными связями. Такие сети необходимо разбивать на подсети, в каждой из которых имеется не более одной обратной связи. На рисунке 8 представлена блок-схема и эквивалентная ей сеть Петри, построенная с помощью описанных выше правил. В них имеется обратная связь от узла e к узлу принятия решения b. Из сети Петри пунктирной рамкой выделена подсеть, охваченная обратной связью. В результате сеть преобразована в линейную с одним непримитивным переходом, изображенным на рисунке 9а в виде прямоугольника. Этот прямоугольник представляет подсеть, представленную на рисунке 9б с обратной связью. Приведенные ниже модули знаний содержат описание линейной сети и ее подсети (рис. 9). Посредством модуля знаний M0 производится установка исходного состояния позиций. Фишка помещается в начальную позицию, а остальные пусты. Такая маркировка позволяет запустить процесс. Модуль M1 производит выполнение перехода a, удаляет фишку из позиции p1 и помещает ее в позицию p2. Модуль: M0 Разработчик: Евгенев Г.Б. Наименование: Установка начальных значений позиций
Модуль: M1 Разработчик: Евгенев Г.Б. Наименование: Выполнение вычисления a
Такая маркировка сети позволяет запустить непримитивный переход bl1. В отличие от переходов a и f, представляющих собой исполняемые модули интегрируемых систем, непримитивный переход, представляющий подсеть, генерируется с помощью средств экспертного программирования в виде метода. Этот метод компонуется из приведенных ниже модулей знаний с идентификаторами Bl. Модуль M3 завершает описание линейной сети Петри, изображенной на рисунке 9а.
Разработчик: Евгенев Г.Б. Наименование: Выполнение вычисления bl1
Модуль: M3 Разработчик: Евгенев Г.Б. Наименование: Выполнение вычисления f
Описание подсети (рис. 9б) также начинается с модуля Bl0, обеспечивающего исходную маркировку. Модуль: Bl0 Разработчик: Евгенев Г.Б. Наименование: Установка начальных значений позиций
Далее следуют два модуля Bl1 и Bl2, описывающих узел принятия решения b. Для определенности в этом и остальных случаях в качестве истинного значения предиката приняты положительные величины соответствующих переменных. Модуль: Bl1 Разработчик: Евгенев Г.Б. Наименование: Принятие решения при положительной величине b
Модуль: Bl2 Разработчик: Евгенев Г.Б. Наименование: Принятие решения при отрицательной величине b
Модули Bl3 и Bl4, аналогичным образом описывают узел принятия решения c. Модуль: Bl3 Разработчик: Евгенев Г.Б. Наименование: Принятие решения при положительной величине c
Модуль: Bl4 Разработчик: Евгенев Г.Б. Наименование: Принятие решения при отрицательной величине c
Выполнение вычислений в переходах d и e задается модулями Bl5 и Bl6. Модуль: Bl5 Разработчик: Евгенев Г.Б. Наименование: Выполнение вычисления d
Модуль: Bl6 Разработчик: Евгенев Г.Б. Наименование: Выполнение вычисления e
Последний модуль Bl7 предназначен для организации циклической работы подсети, обусловленной обратной связью. Цикл организуется при появлении выделенной переменной FinCalc, которая прекращает выполнение программы, когда принимает значение 1. В данном случае цикл прекращается, когда фишка попадает в позицию p9. Модуль: Bl7 Разработчик: Евгенев Г.Б. Наименование: Окончание цикла
Таким образом, разработана методика, позволяющая непрограммирующим пользователям создавать интегрированные прикладные системы, включающие в себя сложные подсистемы. Список литературы 1. Евгенев Г.Б. Системология инженерных знаний: Учеб. пособие для вузов – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. - 520с. 2. Питерсон Дж. Теория сетей Петри и моделирование систем. / Пер. с англ. – М.: Мир, 1984. - 264с.
|
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=523 |
Версия для печати Выпуск в формате PDF (0.95Мб) |
| Статья опубликована в выпуске журнала № 3 за 2005 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Реализация временных рассуждений для интеллектуальных систем поддержки принятия решений реального времени
- Исследовательское проектирование в кораблестроении на основе гибридных экспертных систем
- Компьютерные технологии сегодня: тенденции и прогнозы
- ДИНАМИКА-2 - программа для решения осесимметричных и плоских задач
- Опыт разработки и эксплуатации системы управления базами данных (DBS/R)
Назад, к списку статей



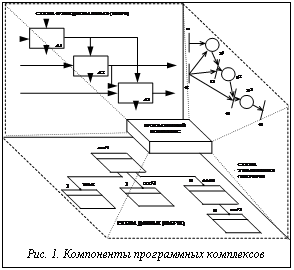 Для построения концептуальных моделей данных в системе международных стандартов имеется стандарт IDEF1X. Нотация этого стандарта (рис. 1) использована для представления схемы данных интегрированного комплекса. Все интегрируемые системы должны выбирать необходимые для своей работы исходные данные из баз данных D и помещать в них результаты.
Для построения концептуальных моделей данных в системе международных стандартов имеется стандарт IDEF1X. Нотация этого стандарта (рис. 1) использована для представления схемы данных интегрированного комплекса. Все интегрируемые системы должны выбирать необходимые для своей работы исходные данные из баз данных D и помещать в них результаты.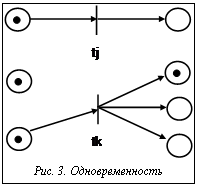 В таблице описаны события и их пред- и постусловия, соответствующие сети Петри, представленной на рисунке 2.
В таблице описаны события и их пред- и постусловия, соответствующие сети Петри, представленной на рисунке 2.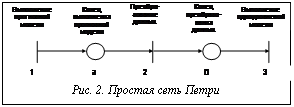 Имеется два варианта отображения недетерминированности запусков переходов в моделировании параллельной системы. Один из них представлен на рисунке 3. В этой ситуации два разрешенных перехода не влияют друг на друга, и любой из них может быть запущен первым. Это называется одновременностью [2].
Имеется два варианта отображения недетерминированности запусков переходов в моделировании параллельной системы. Один из них представлен на рисунке 3. В этой ситуации два разрешенных перехода не влияют друг на друга, и любой из них может быть запущен первым. Это называется одновременностью [2].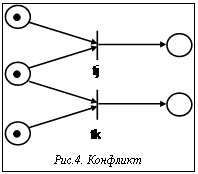 Другая ситуация изображена на рисунке 4. Здесь два разрешенных перехода находятся в конфликте [2]. В итоге может быть запущен только один из них, так как при запуске будет удалена разрешающая фишка из общего входа. Конфликты в правильно построенной сети интегрированной системы недопустимы.
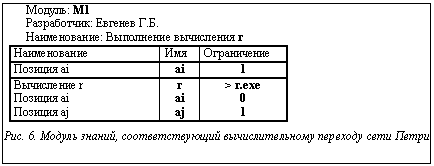
Другая ситуация изображена на рисунке 4. Здесь два разрешенных перехода находятся в конфликте [2]. В итоге может быть запущен только один из них, так как при запуске будет удалена разрешающая фишка из общего входа. Конфликты в правильно построенной сети интегрированной системы недопустимы.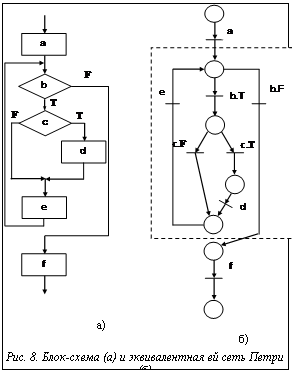 На рисунке 6 представлен модуль знаний, соответствующий вычислительному переходу сети Петри (рис. 5а). Предусловием запуска вычислительного блока является наличие фишки во входной позиции, что представлено как равенство ai=1. Вычислительный блок запускается системной командой (>r.exe) с указанием имени исполняемого файла и пути к нему (при необходимости). После окончания его работы производится изменение состояния позиций: из входной позиции фишка удаляется (ai=0), а в выходную помещается (ak=1).
На рисунке 6 представлен модуль знаний, соответствующий вычислительному переходу сети Петри (рис. 5а). Предусловием запуска вычислительного блока является наличие фишки во входной позиции, что представлено как равенство ai=1. Вычислительный блок запускается системной командой (>r.exe) с указанием имени исполняемого файла и пути к нему (при необходимости). После окончания его работы производится изменение состояния позиций: из входной позиции фишка удаляется (ai=0), а в выходную помещается (ak=1).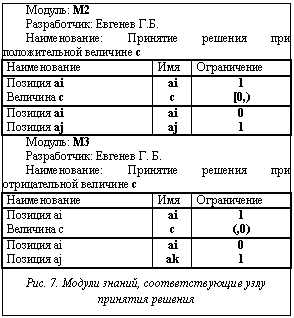
 В соответствии с числом переходов сети Петри на рисунке 5б используются два модуля знаний: один для значения «истина» (T), а другой для значения «ложь» (F). Для определенности в этих модулях знаний истинным является положительное значение величины c.
В соответствии с числом переходов сети Петри на рисунке 5б используются два модуля знаний: один для значения «истина» (T), а другой для значения «ложь» (F). Для определенности в этих модулях знаний истинным является положительное значение величины c.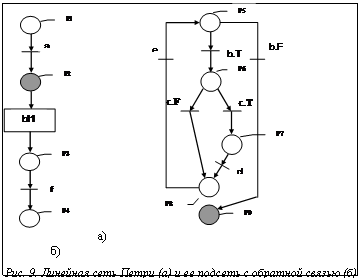 Модуль: M2
Модуль: M2