Особенностью многих комбинаторных задач является проста и наглядность их содержательной постановки и в то же время сложность формализации и решения. Классическим примером подобной задачи является задача коммивояжера, которая состоит в определении такой последовательности однократного посещения всех n-1 пунктов с возвращением в исходный пункт Ак, при которой суммарная длина пройденного пути минимальна. Расстояния cij между каждой парой пунктов Аi Аj известны и заданы матрицей с=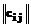 .
.
В комбинаторной постановке задача состоит в поиске кратчайшего маршрута, проходящего через все вершины графа, с возвращением в исходную вершину Aк (вместо L(Bk)=L(‹k,…, i,j,…,k›) для краткости пишется L‹k,…,,i,j,…,k›):
 {Bk},
{Bk},
где Вк= – упорядоченная последовательность номеров пунктов (кортеж), посещаемых коммивояжером при их последовательном обходе; L(Bk) – длина проходимого при этом пути (при постановке в форме задачи математического программирования громоздкость записей значительно возрастет).
– упорядоченная последовательность номеров пунктов (кортеж), посещаемых коммивояжером при их последовательном обходе; L(Bk) – длина проходимого при этом пути (при постановке в форме задачи математического программирования громоздкость записей значительно возрастет).
Поскольку между начальным и конечным пунктами находятся n-1 остальных, то общее число возможных замкнутых маршрутов (циклов) равно (n-1)!, что практически исключает возможность перебора всех возможных вариантов при значениях n, представляющих практический интерес.
К настоящему времени существует достаточно большое число точных и приближенных методов решения задачи коммивояжера. Точные методы [1] требуют больших объемов вычислений, а известные приближенные не гарантируют точность решения, и объем счета остается весьма значительным. Наиболее успешные реализации приближенных алгоритмов, полностью автоматизированные на ЭВМ, связаны с двумя схемами решения: схемой улучшения исходного цикла (схема А) и схемой последовательного построения цикла (схема В).
Предлагаемый метод расширения цикла (МРЦ) ближе примыкает к схеме В, однако отличается от нее тем, что в качестве исходного берется уже готовый цикл с одной промежуточной вершиной:  = ák; j; kñ. На каждом шаге в один из промежутков цикла вставляется номер jt еще незадействованной вершины, при которой обеспечивается минимальное приращение длины цикла
= ák; j; kñ. На каждом шаге в один из промежутков цикла вставляется номер jt еще незадействованной вершины, при которой обеспечивается минимальное приращение длины цикла  и вставляется он в тот промежуток с номером rt , при котором это приращение так же минимально
и вставляется он в тот промежуток с номером rt , при котором это приращение так же минимально  .
.
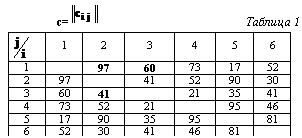
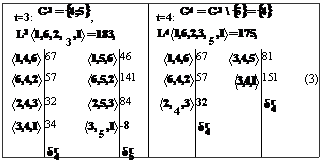 Предлагаемую схему решения проиллюстрируем на модельном примере (табл. 1).
Предлагаемую схему решения проиллюстрируем на модельном примере (табл. 1).
}
Для построения начального минимального цикла может быть выбрана любая пара вершин. Пусть ák; j; kñ = á1,2,1ñ, тогда множество номеров вершин, из которых одна должна быть включена в цикл на первом (t=1) шаге процесса, будет равно  . Приращение
. Приращение 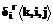 длины цикла
длины цикла  при включении вершины Ai (
при включении вершины Ai (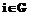 1) в r-й интервал между вершинами с номерами k, j найдется по формуле:
1) в r-й интервал между вершинами с номерами k, j найдется по формуле:
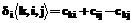 (1)
(1)
Для k=1, i=3, j=2 (табл. 1), например, получим:
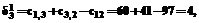 где первые два слагаемых элемента обозначают новую длину маршрута между вершинами Ак и Аj, из которой вычитается прежняя длина (до введения i=3).
где первые два слагаемых элемента обозначают новую длину маршрута между вершинами Ак и Аj, из которой вычитается прежняя длина (до введения i=3).
Расчеты, проведенные для первых двух шагов процесса, удобно представить в виде формулы (2):
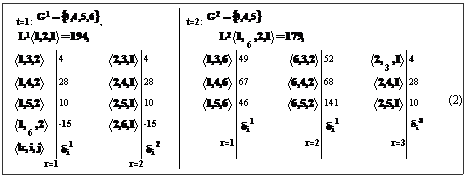
Примечание. Из анализа (2), в частности, следует, что в силу симметрии матрицы c ( ) второй столбец для t=1 можно было бы и не вычислять, так как L(k,j,i)=L(i,j,k), то есть прямой и обратный пути равны. При этом теряется второй вариант решения, отличающийся от первого только направлением движения коммивояжера, что легко восстановить.
) второй столбец для t=1 можно было бы и не вычислять, так как L(k,j,i)=L(i,j,k), то есть прямой и обратный пути равны. При этом теряется второй вариант решения, отличающийся от первого только направлением движения коммивояжера, что легко восстановить.
На последующих двух итерациях в цикл последовательно включаются номера оставшихся вершин j=5 и j=4:
После включения в цикл вершины j=4 на шаге t=4 с учетом примечания получено решение, которое является оптимальным и имеет вид формулы (3):
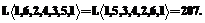 (4)
(4)
Если в качестве начального цикла выбрать B1=á2,1,2ñ, то снова будет получено оптимальное решение, так как на шаге t=1 в (2) только лишь поменяются местами столбцы с вычислениями, а далее процесс не изменится. Более того, если в начальный цикл ввести сразу две промежуточные вершины (например, á1,2,4,1ñ á3,2,6,3ñ, á3,6,2,3ñ, á1,6,5,1ñ и др.), то их упорядоченность совпадет с их порядком в одном из оптимальных решений (4), а, следовательно, не исключает возможности получения правильного решения. Это справедливо только для симметричной матрицы 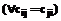 .
.
Таким образом, при симметричной матрице расстояний МРЦ позволяет достаточно эффективно решать задачу коммивояжера, но не гарантирует оптимальности решения. Для получения таких гарантий рассмотрим применение МРЦ для решения задачи с полносвязной, но несимметричной матрицей расстояний с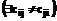 , при этом, если
, при этом, если 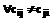 , то можно, в отличие от симметричного случая, говорить об отсутствии двух взаимно противоположных оптимальных циклов. Это, в частности, означает, что в качестве исходного можно брать цикл только с одним промежуточным элементом, чтобы в самом начале не исключить возможность оптимального решения. Схема расчета не меняется, и объем вычислений остается практически таким же.
, то можно, в отличие от симметричного случая, говорить об отсутствии двух взаимно противоположных оптимальных циклов. Это, в частности, означает, что в качестве исходного можно брать цикл только с одним промежуточным элементом, чтобы в самом начале не исключить возможность оптимального решения. Схема расчета не меняется, и объем вычислений остается практически таким же.
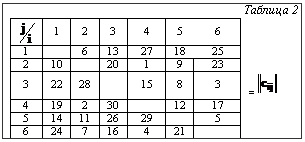
Для матрицы расстояний, представленной в таблице 2, МРЦ получено 15 вариантов решений (для всех возможных сочетаний двух вершин графа, образующих исходный цикл (табл. 3, t=0)). Динамика расширения цикла соответствует элементам, выделенным жирным шрифтом, на каждом шаге процесса.
При случайном (равновероятном) выборе двух элементов для начального цикла вероятность попасть на ошибочный вариант согласно данным таблицы 3, будет равна Рош=4/15»0,27. Если указанным способом наугад выбрать и решить m=3 варианта, то вероятность того, что среди них окажется хотя бы один оптимальный, будет равна:

Примечание. Следует отметить, что три из четырех ошибочных вариантов соответствуют минимальной оценке Lk1 начального цикла Bk1 (жирный шрифт в таблице 3, t=0). Если отмеченная особенность отражает существующую закономерность, то для снижения вероятности получения ошибочного решения Рош, варианты с минимальными оценками Lk1 целесообразно пропускать при выборе очередного начального варианта.
 Полагая, что и для других задач будет существовать вероятность ошибки выбора Pош<1, можно использовать следующую схему расчета. Получив первый вариант решения задачи, не пытаться улучшать его известными методами [1], а перейти к поиску очередного варианта с новым начальным циклом. Так как среднее число попыток до появления оптимального варианта согласно геометрическому закону распределения равно (1-Рош)-1 [2], то, продолжая процесс вычисления вариантов до повторного появления оптимального варианта, в среднем потребуется 2(1-Рош)-1 попыток. В ОЗУ ЭВМ сохраняется только лучший вариант, и в момент получения варианта, совпадающего с ним, процесс прекращается.
Полагая, что и для других задач будет существовать вероятность ошибки выбора Pош<1, можно использовать следующую схему расчета. Получив первый вариант решения задачи, не пытаться улучшать его известными методами [1], а перейти к поиску очередного варианта с новым начальным циклом. Так как среднее число попыток до появления оптимального варианта согласно геометрическому закону распределения равно (1-Рош)-1 [2], то, продолжая процесс вычисления вариантов до повторного появления оптимального варианта, в среднем потребуется 2(1-Рош)-1 попыток. В ОЗУ ЭВМ сохраняется только лучший вариант, и в момент получения варианта, совпадающего с ним, процесс прекращается.
Например, полагая, что вероятность ошибки Рош=0,5, ожидаемое число вариантов равно m = 2×(1 - Рош)-1=4, при этом достоверность полученного таким путем решения будет равна:

Для повышения надежности результата процесс можно продолжить до появления третьего решения, совпадающего с лучшим, что существенно не увеличит объем вычислений. Непосредственно моделированием с использованием таблицы 3 можно убедиться в справедливости полученной оценки, при этом до повторного появления правильного решения в среднем потребуется проверка m=2×(1-0,27)-1 »2,6, то есть двух-трех вариантов.
Для моделирования без ЭВМ достаточно записать числа от 1 до 6 на шести бумажках. Выбирая наугад две из них, по написанным на них числам (пусть это 2 и 5) формируется начальный цикл L(2,5,2) (или L(5,2,5)). По таблице 3 проверяется, является ли решение оптимальным. Опыты продолжают до появления двух совпадающих решений.
Получим оценки требуемого объема счета и памяти ОЗУ для получения одного варианта.
На t-м шаге процесса имеется t+1 интервалов для подстановки в них поочередно каждого из оставшихся n-(t+1) номеров вершин. Следовательно, на t-м шаге потребуется вычислить (t+1)×(n-(t+1)) значений поправок 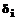 (1) и выбрать из них наименьшую. Для вычисления
(1) и выбрать из них наименьшую. Для вычисления 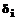 (1) требуется две операции сложения и одна операция сравнения с предыдущей оценкой. Суммируя по всем n-2 шагам, получим требуемое число элементарных операций:
(1) требуется две операции сложения и одна операция сравнения с предыдущей оценкой. Суммируя по всем n-2 шагам, получим требуемое число элементарных операций:
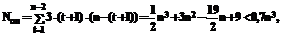
 . (5)
. (5)
Так, например, для расчета варианта задачи с n=1000 пунктами при быстродействии 106 оп/с потребуется 10 мин.
 Требуемый объем оперативной памяти определится необходимостью хранения n×(n-1) значащих элементов матрицы c и n+2 ячеек должно быть выделено для хранения элементов расширяющегося цикла и его оценки Lt. Промежуточная информация практически отсутствует, так как в ходе расчетов на каждом шаге из массива (2) хранится только один (минимальный) элемент
Требуемый объем оперативной памяти определится необходимостью хранения n×(n-1) значащих элементов матрицы c и n+2 ячеек должно быть выделено для хранения элементов расширяющегося цикла и его оценки Lt. Промежуточная информация практически отсутствует, так как в ходе расчетов на каждом шаге из массива (2) хранится только один (минимальный) элемент 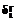 и связанные с ним величины.
и связанные с ним величины.
Сравнение с аналогичными оценками, например, для точного метода Хелда, Карпа и Беллмана (~n2×2n-1–операций, ~n2n-1-память), приведенными в [1], а также с соответствующими оценками для наилучших из приближенных алгоритмов (алг. Лина ~3,5n3×(n-4)!, [1]), позволяет рассчитывать на высокую эффективность МРЦ.
Порядок решения задачи МРЦ может быть записан в виде следующего алгоритма:
1o. Читать  ,n.
,n.
2o. Принять номер начального варианта k равным номеру вершины А1 (k=1).
3o. Записать начальный цикл 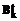 , его оценку
, его оценку  и множество номеров свободных (не включенных еще в цикл) вершин
и множество номеров свободных (не включенных еще в цикл) вершин 
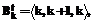

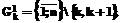
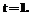
4o. Пронумеровать промежутки (дуги) в текущем цикле  (
(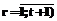 и записать номера граничных вершин каждого промежутка: r – порядковый номер промежутка в цикле (слева направо); jr-1, jr – соответственно номера левой и правой вершин r-го промежутка в цикле.
и записать номера граничных вершин каждого промежутка: r – порядковый номер промежутка в цикле (слева направо); jr-1, jr – соответственно номера левой и правой вершин r-го промежутка в цикле.
5o. На t-м шаге для r-го промежутка вычислить приращение длины цикла при включении в промежуток r j-й вершины:
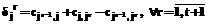 ,
, 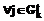 .
.
6o. Определить номер расширяемого промежутка rt и включаемой в него вершины jt из условия:
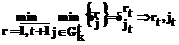 (
( ).
).
7o. Пересчитать текущий цикл, его оценку и множество  :
:

 ,
, 
8o. Если 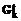 ¹Æ – идти к 4o.
¹Æ – идти к 4o.
9o. Если 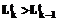 – принять k=k+1, идти к 3o.
– принять k=k+1, идти к 3o.
10o. Если  – запомнить новое решение
– запомнить новое решение 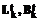 и перейти к 3o.
и перейти к 3o.
11o. Писать 

 .
.
12о. Конец.
Пункты 5o, 6o выполняются совместно, так что по мере вычисления элементов 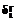 в памяти ЭВМ хранится только меньший элемент
в памяти ЭВМ хранится только меньший элемент  , а также rt, jt.
, а также rt, jt.
При выполнении пункта 9o полагается, что для задач большой размерности необходимое условие k£n-2 будет соблюдено.
В пункте 11o учтена возможность получения одного экстремума при разных решениях (кортежах) 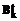 и
и 
Отметим возможность некоторых обобщений метода, особенность оптимального решения и некоторые проблемные вопросы.
Метод практически не изменяется, если требуется найти гамильтонов (полный) путь между двумя различными вершинами. В начальном маршруте промежуточным берется номер любой другой вершины.
В оптимальном цикле упорядоченность номеров вершин не меняется при выходе коммивояжера из любого другого пункта и возвращении в него же.
Имея оптимальный цикл, легко решается вопрос из какого пункта следует начать обход остальных, что-бы длина пути до прибытия на последний пункт (без возвращения в исходный) была минимальной. Для решения задачи следует найти 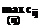 из всех дуг, составляющих оптимальный цикл, и в качестве исходного выбрать пункт, при котором наиболее длинная дуга окажется последней; то есть пункт, соответствующий концу наиболее длинной дуги. Так, для оптимального цикла имеем:
из всех дуг, составляющих оптимальный цикл, и в качестве исходного выбрать пункт, при котором наиболее длинная дуга окажется последней; то есть пункт, соответствующий концу наиболее длинной дуги. Так, для оптимального цикла имеем:

L=13+8+5+4+2+10+=42 Þmax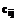 =
=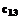 =13.
=13.
Следовательно, обход может быть закончен на 13 ед. раньше, если обход начать из А3 и закончить в А1:
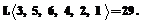
В заключение отметим, что поскольку объем счета при МРЦ близок к минимально возможному (наиболее простой алгоритм – на каждом шаге идти к ближайшему пункту [1] – для получения варианта решения требует cn2 < 0,5 n2 операций сравнения) (см. (5)) и при этом гарантируется требуемая достоверность решения, то проблема решения классической задачи коммивояжера в значительной мере теряет свою актуальность. Однако может быть предложена более общая постановка задачи, в которой при обходе всех пунктов в каждый из них коммивояжер должен доставить cj тонн 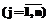 груза. Оптимальный маршрут (цикл) должен соответствовать минимуму энергозатрат в тоннокилометрах. Частный случай этой задачи ("сj=0 и вес транспортного средства с0¹0) соответствуют классической задаче коммивояжера.
груза. Оптимальный маршрут (цикл) должен соответствовать минимуму энергозатрат в тоннокилометрах. Частный случай этой задачи ("сj=0 и вес транспортного средства с0¹0) соответствуют классической задаче коммивояжера.
Обобщенная задача еще более усложняется, если грузоподъемность транспортного средства не позволяет развезти все грузы за один заезд.
Возможные подходы к решению обобщенной задачи к настоящему времени нам неизвестны, как неизвестны и методы решения рассмотренных задач при неполносвязной матрице расстояний между пунктами.
Список литературы
1. Основы теории оптимального управления. //Под ред. В.Ф. Кротова.–М.: Высш. шк., 1990.–430 с.
2. Гмурман В. Е. Теория вероятностей и математическая статистика. – М.: Высш. шк., 1997. – 479 с.



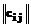 .
. {Bk},
{Bk}, – упорядоченная последовательность номеров пунктов (кортеж), посещаемых коммивояжером при их последовательном обходе; L(Bk) – длина проходимого при этом пути (при постановке в форме задачи математического программирования громоздкость записей значительно возрастет).
– упорядоченная последовательность номеров пунктов (кортеж), посещаемых коммивояжером при их последовательном обходе; L(Bk) – длина проходимого при этом пути (при постановке в форме задачи математического программирования громоздкость записей значительно возрастет). = ák; j; kñ. На каждом шаге в один из промежутков цикла вставляется номер jt еще незадействованной вершины, при которой обеспечивается минимальное приращение длины цикла
= ák; j; kñ. На каждом шаге в один из промежутков цикла вставляется номер jt еще незадействованной вершины, при которой обеспечивается минимальное приращение длины цикла  и вставляется он в тот промежуток с номером rt , при котором это приращение так же минимально
и вставляется он в тот промежуток с номером rt , при котором это приращение так же минимально  .
.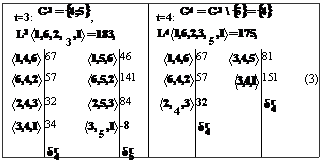 Предлагаемую схему решения проиллюстрируем на модельном примере (табл. 1).
Предлагаемую схему решения проиллюстрируем на модельном примере (табл. 1). . Приращение
. Приращение 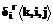 длины цикла
длины цикла  при включении вершины Ai (
при включении вершины Ai (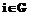 1) в r-й интервал между вершинами с номерами k, j найдется по формуле:
1) в r-й интервал между вершинами с номерами k, j найдется по формуле: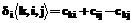 (1)
(1)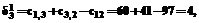 где первые два слагаемых элемента обозначают новую длину маршрута между вершинами Ак и Аj, из которой вычитается прежняя длина (до введения i=3).
где первые два слагаемых элемента обозначают новую длину маршрута между вершинами Ак и Аj, из которой вычитается прежняя длина (до введения i=3).
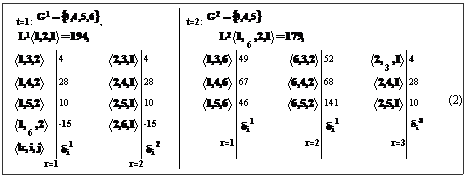
 ) второй столбец для t=1 можно было бы и не вычислять, так как L(k,j,i)=L(i,j,k), то есть прямой и обратный пути равны. При этом теряется второй вариант решения, отличающийся от первого только направлением движения коммивояжера, что легко восстановить.
) второй столбец для t=1 можно было бы и не вычислять, так как L(k,j,i)=L(i,j,k), то есть прямой и обратный пути равны. При этом теряется второй вариант решения, отличающийся от первого только направлением движения коммивояжера, что легко восстановить.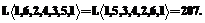 (4)
(4)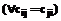 .
.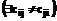 , при этом, если
, при этом, если 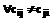 , то можно, в отличие от симметричного случая, говорить об отсутствии двух взаимно противоположных оптимальных циклов. Это, в частности, означает, что в качестве исходного можно брать цикл только с одним промежуточным элементом, чтобы в самом начале не исключить возможность оптимального решения. Схема расчета не меняется, и объем вычислений остается практически таким же.
, то можно, в отличие от симметричного случая, говорить об отсутствии двух взаимно противоположных оптимальных циклов. Это, в частности, означает, что в качестве исходного можно брать цикл только с одним промежуточным элементом, чтобы в самом начале не исключить возможность оптимального решения. Схема расчета не меняется, и объем вычислений остается практически таким же.
 Полагая, что и для других задач будет существовать вероятность ошибки выбора Pош<1, можно использовать следующую схему расчета. Получив первый вариант решения задачи, не пытаться улучшать его известными методами [1], а перейти к поиску очередного варианта с новым начальным циклом. Так как среднее число попыток до появления оптимального варианта согласно геометрическому закону распределения равно (1-Рош)-1 [2], то, продолжая процесс вычисления вариантов до повторного появления оптимального варианта, в среднем потребуется 2(1-Рош)-1 попыток. В ОЗУ ЭВМ сохраняется только лучший вариант, и в момент получения варианта, совпадающего с ним, процесс прекращается.
Полагая, что и для других задач будет существовать вероятность ошибки выбора Pош<1, можно использовать следующую схему расчета. Получив первый вариант решения задачи, не пытаться улучшать его известными методами [1], а перейти к поиску очередного варианта с новым начальным циклом. Так как среднее число попыток до появления оптимального варианта согласно геометрическому закону распределения равно (1-Рош)-1 [2], то, продолжая процесс вычисления вариантов до повторного появления оптимального варианта, в среднем потребуется 2(1-Рош)-1 попыток. В ОЗУ ЭВМ сохраняется только лучший вариант, и в момент получения варианта, совпадающего с ним, процесс прекращается.
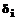 (1) и выбрать из них наименьшую. Для вычисления
(1) и выбрать из них наименьшую. Для вычисления 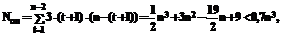
 . (5)
. (5)
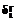 и связанные с ним величины.
и связанные с ним величины. ,n.
,n.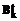 , его оценку
, его оценку  и множество номеров свободных (не включенных еще в цикл) вершин
и множество номеров свободных (не включенных еще в цикл) вершин 
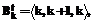

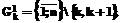
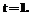
 (
(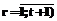 и записать номера граничных вершин каждого промежутка: r – порядковый номер промежутка в цикле (слева направо); jr-1, jr – соответственно номера левой и правой вершин r-го промежутка в цикле.
и записать номера граничных вершин каждого промежутка: r – порядковый номер промежутка в цикле (слева направо); jr-1, jr – соответственно номера левой и правой вершин r-го промежутка в цикле.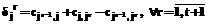 ,
, 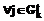 .
.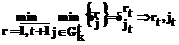 (
( ).
). :
:
 ,
, 
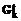 ¹Æ – идти к 4o.
¹Æ – идти к 4o.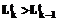 – принять k=k+1, идти к 3o.
– принять k=k+1, идти к 3o. – запомнить новое решение
– запомнить новое решение 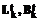 и перейти к 3o.
и перейти к 3o.

 .
. , а также rt, jt.
, а также rt, jt.
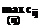 из всех дуг, составляющих оптимальный цикл, и в качестве исходного выбрать пункт, при котором наиболее длинная дуга окажется последней; то есть пункт, соответствующий концу наиболее длинной дуги. Так, для оптимального цикла имеем:
из всех дуг, составляющих оптимальный цикл, и в качестве исходного выбрать пункт, при котором наиболее длинная дуга окажется последней; то есть пункт, соответствующий концу наиболее длинной дуги. Так, для оптимального цикла имеем:
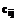 =
=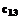 =13.
=13.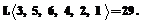
 груза. Оптимальный маршрут (цикл) должен соответствовать минимуму энергозатрат в тоннокилометрах. Частный случай этой задачи ("сj=0 и вес транспортного средства с0¹0) соответствуют классической задаче коммивояжера.
груза. Оптимальный маршрут (цикл) должен соответствовать минимуму энергозатрат в тоннокилометрах. Частный случай этой задачи ("сj=0 и вес транспортного средства с0¹0) соответствуют классической задаче коммивояжера.