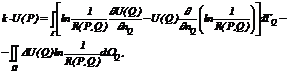Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Компьютерное моделирование электрического поля в прямоугольных областях
Аннотация:
Abstract:
| Авторы: Иванов В.Т. () - , Нугуманов Р.Г. () - , Щербинин С.А. () - | |
| Количество просмотров: 8268 |
Версия для печати Выпуск в формате PDF (1.25Мб) |
Bсе больше отраслей экономики используют компьютерные разработки. Во многом это связано с большими затратами на эксперименты и cо сложностью их организации. Одним из таких примеров может служить рассматриваемая задача моделирования электрического поля. Необходимость таких расчетов возникает при моделировании электролитического получения многих легких металлов (Mg, Al), при этом пузырьки появляются в результате электролитической диссоциации молекул. Пузырьки, выделяющиеся на одном из электродов, не проводят электрический ток, то есть изолируют часть поверхности электрода, что приводит к изменению распределения электрического тока. Возникающее увеличение разности потенциалов в электролизере приводит к существенному увеличению энергозатрат.
Найти радиус пузырька в момент времени t можно с помощью уравнения [1]:
где P0 – внешнее давление; Pt – давление газа в газовом пузырьке; d – поверхностное натяжение, mж - вязкость жидкости, R – радиус газового пузырька, e=(rж–rГ)/rж, rж и rГ – плотности жидкости и газа соответственно. Таким образом, для расчета поля U(x,y,t)=U(x,y) в момент времени t мы имеем краевую задачу для уравнения Пуассона в области, граница которой меняется при возрастании R по некоторому закону. Глобальный алгоритм решения поставленной задачи выглядит следующим образом: для фиксированного момента времени t с помощью метода конечных разностей получим значение радиуса пузырька R (или радиусы нескольких пузырьков Ri), далее для полученного значения R с помощью метода граничных элементов (МГЭ) находим потенциал и плотность тока на границе и внутри расчетной области. В МГЭ происходит предварительный переход от исходной краевой задачи для дифференциального уравнения, описывающей некоторый процесс к соотношениям, связывающим неизвестные функции на границе области. При применении формулы Грина в данной задаче МГЭ позволяет рассматривать и граничное условие I рода на некоторых участках границы. Интегральное представление Грина для двухмерного случая имеет вид [2]:
где R(P,Q) – расстояние между точками P и Q в области W, k=2p внутри области W, k=p на границе области Г. Созданы версии программы для DOS и для Windows-95 (98). Тестовые и методические расчетыВыбор шага сетки. При уменьшении шага сетки уменьшается погрешность аппроксимации. Рассмотрим влияние выбора шага сетки на результаты расчетов. В случае вертикальных электродов колебания максимальных значений потенциала на катоде и плотности тока на аноде по оси Ox при изменении шага в 2–4 раза составляют порядок 10–7; колебания максимальных значений по оси Oy при изменении шага на 50 % раза составляют 0.8 % и 7 % соответственно, поэтому шаг по оси Oy надо брать минимальный. Выбор способа расчета в угловых точках. В угловых точках нарушается гладкость границы, и в МГЭ при решении уравнений невозможно найти производную по нормали, поэтому рассматривались два случая: 1) угловая точка игнорировалась, 2) угловая точка сглаживалась с помощью дуги окружности с радиусом 10–5. Отклонение потенциала и плотности составило 10–7 и 10–6 соответственно. Хотя отклонение несущественно, для применения теории угловые точки необходимо сглаживать. Исходными данными для работы с программой являются размеры области, размеры электродов, плотность тока, коэффициент электропроводности. Выходные данные – значения плотности тока и потенциала на электродах, которые выводятся на монитор ПК; значения плотности тока и потенциала на всех границах, которые выводятся в файл данных; потенциал внутри области, выводимый вместе с координатами в другой файл данных, который затем использует графический пакет. Основное назначение описанной программы – проведение серий расчетов при различных исходных данных и оценка реакции модели на их изменение. Для визуализации результатов была разработана программа, позволяющая анализировать и сравнивать на мониторе графики плотности тока, потенциала, соответствующие различным вариантам. Список литературы1. Ивановский Л.Е., Лебедев В.А., Некрасов В.Н. Анодные процессы в расплавленных галогенидах. -М.: Наука, 1983. 2. Бенержди П., Баттерфилд Р. Методы граничных элементов в прикладных науках. - М.: Мир, 1984. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=921 |
Версия для печати Выпуск в формате PDF (1.25Мб) |
| Статья опубликована в выпуске журнала № 1 за 1999 год. |
Назад, к списку статей



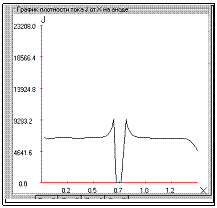 Рассмотрим модель электролитической ячейки прямоугольной области с вертикально расположенными электродами. В этой области ставится задача расчета электрического поля, причем область считаем однородной. На катоде задается плотность подводимого тока, на аноде задается нулевой электрический потенциал. На остальных участках границы электрический ток не протекает, и на них ставится условие электроизолированности. На аноде допускается выделение пузырьков с границей формы полуокружностей, количество и полуоси которых задаются. Таким образом, для расчета электрического поля в описанной области получим смешанную краевую задачу для уравнения Лапласа относительно потенциала U(x,y).
Рассмотрим модель электролитической ячейки прямоугольной области с вертикально расположенными электродами. В этой области ставится задача расчета электрического поля, причем область считаем однородной. На катоде задается плотность подводимого тока, на аноде задается нулевой электрический потенциал. На остальных участках границы электрический ток не протекает, и на них ставится условие электроизолированности. На аноде допускается выделение пузырьков с границей формы полуокружностей, количество и полуоси которых задаются. Таким образом, для расчета электрического поля в описанной области получим смешанную краевую задачу для уравнения Лапласа относительно потенциала U(x,y).