Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Методы редукции графов в задачах реструктуризации задолженности предприятий
Аннотация:
Abstract:
| Авторы: Колесник Г.В. () - , Катулев А.Н. (katulevan@yandex.ru) - Тверской государственный технический университет (профессор), Тверь, Россия, доктор технических наук, Михеев В.Н. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 14866 |
Версия для печати Выпуск в формате PDF (1.58Мб) |
В настоящее время в региональной экономике сложилась ситуация, характеризуемая наличием задолженностей между предприятиями, бюджетами различных уровней и внебюджетными фондами, что делает актуальным поиск путей реструктуризации задолженностей с целью обоснованного снижения их общего уровня. В математическом плане схема взаимных задолженностей предприятий, бюджетов и внебюджетных фондов может быть представлена в виде взвешенного ориентированного графа. Анализ такого графа известными методами [2] с целью выработки рекомендаций по реструктуризации задолженности при большом количестве предприятий весьма затруднен и практически нереализуем даже на современных ПЭВМ. Поэтому возникает задача разработки метода редукции исходного графа задолженностей к однозначно эквивалентному графу в смысле долговых обязательств между предприятиями, бюджетами и внебюджетными фондами, а именно, к взвешенному ориентированному графу наиболее простой структуры. В [1] изложен один из методов реструктуризации подобного рода системы и выработки рекомендаций по погашению взаимной задолженности предприятий. Этот метод опирается на предположение о том, что орган управления может произвольным образом изменять имеющиеся величины задолженностей. Однако в реальных экономических системах возможности органов управления по реструктуризации долгов могут существенно различаться. Цель настоящей статьи заключается в разработке программно реализуемого метода реструктуризации графа задолженностей предприятий к графу с минимальным уровнем задолженности, применимого при различном уровне полномочий органов управления. Будем рассматривать ориентированный граф с весами, заданными на ребрах: Г = (U, V, сг(v)), где U – множество вершин графа, каждая вершина u Î U соответствует некоторому предприятию, бюджету или фонду; VÍ U´U – множество ребер графа; v = (ui, uj) Î V соответствует задолженности предприятия ui предприятию uj, при этом величина задолженности определяется функцией cГ(v) : V1 ® R+. Здесь V1 – множество ребер такое, что соответствующий ориентированный граф (U, V1) полный. При этом будем полагать cГ(v) = 0 тогда и только тогда, когда v Ï V. Такое задание весовой функции необходимо нам для корректного сравнения уровней задолженности на графах с различными множествами ребер, описывающих эквивалентные схемы неплатежей. В заданной таким образом схеме полустепень исхода вершины u Î U deg–(u) представляет собой общую задолженность предприятия, полустепень захода deg+(u) – общую задолженность клиентов предприятию, а степень вершины deg(u) = deg+(u) – deg–(u) – баланс задолженности предприятия. Последний показатель может рассматриваться как индикатор рентабельности предприятия в условиях неплатежей: в случае отрицательного баланса, даже при условии возвращения долгов клиентами, предприятие не сможет погасить собственной задолженности. В случае его неотрицательности соответствующее предприятие, даже при большой по абсолютной величине задолженности, может рассматриваться как рентабельное, так как при возврате долгов клиентами оно будет в состоянии погасить собственные долги и получить некоторую прибыль. Определим общий уровень задолженности Q(Г) как сумму весов всех ребер графа Г:
Тогда задача отыскания схемы неплатежей минимального уровня задолженности сводится к задаче отыскания графа Г*=(U,V*, cГ*(v)), имеющего минимальное значение Q(Г*): Q(Г) ® Очевидно, граф Г* должен отвечать ряду ограничений, вытекающих из физической сущности неплатежей, и не может быть выбран произвольным образом. Определение. Назовем графы Г и Г' эквивалентными, если множества вершин в них совпадают и выполнены следующие условия: cГ(v) ³ 0; cГ¢¢(v) ³ 0; (3) deg(u)|Г¢¢ = deg(u)| Г¢ ; "u Î U; " Г'. (4) Первое из указанных условий устанавливает неотрицательность величин задолженностей, второе – постоянство балансов задолженности каждой вершины. Будем отыскивать решение задачи (2) во множестве графов, эквивалентных исходному графу Г. Как указывалось выше, возможности органов управления также могут накладывать различные ограничения на структуру множества допустимых решений, определяющиеся тем, что орган управления имеет право либо только уменьшать задолженности предприятий, либо увеличивать часть задолженностей за счет уменьшения других, либо распоряжаться задолженностями произвольным образом, в том числе создавать новые, не нарушая условий эквивалентности (3), (4). Формализованное описание полномочий органа управления представляет собой ограничения на функцию c Г¢¢(v) вида: c Г¢¢(v) £ g(v); " v Î Y, (5) где g(v) – некоторая заданная функция; Y Í V1 – некоторое множество ребер. В частности, полагая g(v) = c Г¢(v); Y = V1, получаем условия, при которых орган управления имеет право только уменьшать величины задолженностей предприятий. Аналогичным образом могут быть получены другие группы ограничений. Задача (2) с ограничениями (3-5) представляет собой задачу линейного программирования, количество переменных в которой может достигать n2, где n = |U|, и решение ее традиционными методами практически невозможно при большом количестве вершин. Ниже приводится ряд вычислительных методов, позволяющих частично или полностью решать данную задачу более эффективным образом. Редукция к графу без циклов Наиболее простым из эквивалентных преобразований графа является удаление в нем замкнутых циклов. Данное преобразование имеет очевидную физическую интерпретацию – проведение взаимозачета между предприятиями. На практике соответствующая схема задолженностей легко анализируется при небольшом количестве предприятий, когда циклическая связь явно прослеживается. Однако реальная схема может охватывать сотни или тысячи предприятий, отслеживание циклических связей между которыми возможно лишь с использованием средств вычислительной техники. Структура соответствующего алгоритма включает в себя следующие операции. 1. В исходном графе Г отыскивается замкнутый цикл S Í V. Для решения данной задачи существует ряд методов, изложенных, например, в [2]. Если цикл не найден, то алгоритм заканчивает работу. 2. Отыскивается множество ребер: Vo = {vo Î S | c Г¢(vo) = co = min(c Г¢(v) | v Î S)}. 3. Строится новый граф Г', в котором удалены все ребра, входящие в Vo (при этом c Г¢¢(v) = 0 " vÎVo), а веса остальных ребер vÎS уменьшены на величину co. Так как со > 0, то в полученном таким образом графе Г' общий уровень задолженности уменьшится: Q(Г') = Q(Г) – com < Q(Г), здесь m – количество ребер в цикле S. Эквивалентность данного преобразования утверждается следующей леммой. Лемма 1. Граф Г', полученный в результате однократного применения алгоритма удаления циклов, эквивалентен графу Г. Доказательство. Условие (3) выполнено в силу co £ c Г¢(v); "nÎS. Очевидно, что данное преобразование не изменяет степеней вершин, не инцидентных ребрам из множества S. Пусть uÎU инцидентна некоторому ребру vÎS. Тогда: deg(u)|Г¢¢= = = где k – число ребер vÎS, входящих в вершину u. Аналогично показывается, что deg–(u)|Г¢¢ = = deg–(u)|Г¢ – mco, m – число ребер vÎS, выходящих из u. По свойствам замкнутых циклов для любого ребра vÎS, выходящего из вершины u, найдется ребро v'ÎS, входящее в нее, и наоборот, поэтому m=k, откуда вытекает выполнение условия (4). Изложенный алгоритм является самым простым и реализует весьма ограниченные возможности по редукции исходного графа: из системы изымаются только те нагрузки (долги), которые предприятие опосредованно оплачивает самому себе, и не затрагивается остальная часть долгов. Например, рассмотрим граф на рисунке 1. Он не содержит циклов, поэтому не может быть упрощен при помощи описанного алгоритма.
Принцип формирования кратчайшего пути Вернемся к графу на рисунке 1. Согласно ему предприятие u1 непосредственно должно u5 40 единиц. Но, помимо этого, u1 должно u5 100 единиц через цепь u1 ® u2 ® u3 ® u4 ® u5. Удалим эти 100 единиц из окружной цепи, то есть перераспределим нагрузки ребер следующим образом: уменьшим вес каждого ребра в цепи u1 ® ® u2 ® u3 ® u4 ® u5 на 100 единиц и увеличим непосредственный долг u1 предприятию u5 на 100 единиц (рис. 2). Видно, что это эквивалентное преобразование. При этом уровень задолженности в полученном графе снизится с 760 до 460 единиц. В общем виде структура данной процедуры состоит в следующем. 1. Для заданной пары вершин (u1, u2) отыскиваются все пути {Li}, соединяющие их с длинами li. 2. Отыскивается путь L0 минимальной длины l0. 3. Для " Li ¹ L0 отыскивается 4. Строится новый граф Г' = (U, V', cг'(v)): " v Î Li ¹ L0: cг'(v) = cг(v) – Общий уровень нагрузки в полученном графе: Q(Г') = Q(Г) + = Q(Г) = Q(Г) так как Таким образом, отыскание в графе пути перемещения долга, имеющего наименьшую длину, снижает общий уровень нагрузки Q(Г). Лемма 2. Г' эквивалентен Г. Доказательство. Очевидно, алгоритм не меняет степеней вершин, не инцидентных ребрам из {Li}. Если u – промежуточная вершина, инцидентная ребрам из { Li }, то для любого входящего в нее ребра vÎ Li найдется некоторое ребро v'Î Li, выходящее из u. Тогда deg+(u) и deg–(u) изменятся на одну и ту же величину при изменении весов ребер v и v', поэтому deg(u) останется постоянной. Для вершины u1 имеем: Deg–(u1)|г'= + = deg+(u1) не изменяется, так как u1 – начальная вершина путей Li. Тогда deg(u1) также не изменится. Проводя аналогичные рассуждения для u2, получим, что условия эквивалентности (3), (4) выполнены для всех вершин. Лемма 3. Граф, являющийся оптимальным решением задачи (2)-(5), где g(v) = 0; Y = V1\V, содержит для каждой пары вершин (u1, u2) не более одного пути, соединяющего их. Доказательство. Действительно, если Г* содержит более одного пути, соединяющего вершины u1 и u2, то, применив к нему описанный выше алгоритм, получим эквивалентный граф, содержащий только один путь между u1 и u2, и с уровнем задолженности, не превышающим Q(Г*). Теорема 1. Граф Г*, полученный согласно методу кратчайшего пути на некотором множестве дуг W, принадлежит множеству оптимальных решений задачи (2)-(5), где g(v) = cГ(v); Y = V1\W. Доказательство. Согласно лемме 2 Г* является допустимым решением задачи (2)-(4). Кроме того, он удовлетворяет ограничению (5), так как в алгоритме не изменяются веса ребер vÏW. Пусть Г0 с уровнем задолженности Q0 – оптимальное решение задачи, Г0 ¹ Г*. В силу леммы 2 для каждой пары вершин в Г0 содержится не более одного пути из W, соединяющего их. Тогда в графе Г0 имеется пара вершин (u1, u2), связанных путем LÎ{Li}, таким, что L ¹ L0 Î Г*. Пусть v0 = arg min {c Г0(v) | vÎL}. Рассмотрим граф Г1, в котором: V1 = V CГ1(v) = cГ0(v) cГ0(v0); vÎL; c Г1(v) = c Г0(v0); vÎL0. В силу леммы 2 Г1 эквивалентен Г0, при этом уровень задолженности: Q(Г1) = Q(Г0) + = Q(Г0) – (l – l0)c0, где с0 = с Г0(v0), l, l0 – длины путей L и L0 соответственно. Отсюда Q(Г1) £ Q(Г0), так как L0 – путь наименьшей длины. Проводя аналогичные рассуждения для всех не совпадающих путей в графах Г0 и Г*, а их число конечно, прийдем в результате к графу Г*. Тогда Q(Г*) £ Q(Г0), то есть Г* – оптимальное решение задачи. Рассмотрим случай, когда W = V1 – множество дуг, такое, что соответствующий ориентированный граф Г1 = (U, V1) является полным. Так как исходное множество дуг VÍV1, оптимум на множестве V будет не меньше, чем оптимум на V1, то минимальный возможный уровень нагрузки в системе будет достигаться на V1.
Рассмотрим граф на рисунке 3. Он получен из графа рисунка 2 при помощи того же алгоритма, только в качестве допустимых рассматривались любые возможные пути перемещения задолженности. В нем введена новая задолженность u2 ® u5, что позволило снизить общий уровень нагрузки графа до величины 320 единиц. Согласно теореме 1 данный метод дает оптимальное решение задачи (2-5) при g(v) = cГ(v); " v Ï V1. Однако V1 – это множество всех возможных ребер графа, поэтому в данном случае в задаче (2-4) не накладывается никаких ограничений на действия органа управления по реструктуризации задолженностей. Определим величину нагрузки на оптимальном решении. Рассмотрим множества U+, U– и U0 вершин гра-фа Г, имеющих соответственно положительную, отрицательную либо нулевую степень. Очевидно, первый тип вершин представляет собой предприятия-доноры, второй – должников, третий – предприятия с нулевым балансом задолженности. Теорема 2. Общий уровень нагрузки на оптимальном решении задачи (2)-(4) равен:
Доказательство проведем в два этапа. Сначала докажем, что общий уровень задолженности в системе не может быть меньше Q*, затем – что он достигается при решении задачи (2-4). Пусть Q < Q*. Тогда из условия:
С другой стороны, из (1):
Тогда:
что противоречит неотрицательности величин deg+(u) и deg–(u). Таким образом, уровень задолженности в системе не может быть меньше величины Q*. Для второй части доказательства потребуется Лемма 4. Оптимальное решение задачи (2)-(4) не содержит путей с длиной, большей 1. Доказательство. Предположим, что это не так, то есть в графе есть путь длины l > 1. Для определенности предположим, что l = 2. Тогда путь имеет вид u1 ® u2 ® u3. Пусть cГ(u1® u2) = c1, cГ(u2 ® u3) = c2. Предположим, что c1 > с2. Рассмотрим граф Г' = (U, V', c'(v)), в котором V' = V Очевидно, данное преобразование не изменило степени вершин, то есть Г' эквивалентен Г. При этом общий уровень задолженности: Q' = Q – c1 – c2 + (c1 – c2) + c2 = Q – c2 < Q. Таким образом, мы нашли новый граф, удовлетворяющий условиям задачи (1-3), с меньшим значением функционала, то есть исходный граф был не оптимален. Утверждение доказано для l = 2. В случае l > 2 выделим в цепи участок длины 2 и проведем для него указанные выше рассуждения. При этом получим участок длины не более 1, то есть длина всей цепи станет не более (l-1). Вернемся теперь к доказательству теоремы. Пусть Q > Q*. Тогда из (6), (7):
Последнее неравенство возможно, если в системе имеется положительная задолженность либо должнику (первое слагаемое), либо изолированному предприятию (второе слагаемое), либо задолженность предприятия-донора (третье слагаемое). Видно, что любой из данных случаев влечет наличие в графе пути длины, большей 1, поэтому согласно лемме 4 данный уровень задолженности не может быть минимальным. Таким образом, данный метод позволяет отыскивать граф Г*, эквивалентный исходному, имеющий минимальный возможный уровень нагрузки Q(Г*). Характерным свойством Г* является отсутствие посредников в платежах, при этом все его вершины будут являться либо источниками, либо стоками, либо изолированными вершинами, а все цепи будут иметь длину 1. Как уже указывалось, задача (2-5) для Y = V1 содержит n2 свободных переменных, поэтому ее решение традиционными методами практически невозможно при больших n. Однако доказанные выше утверждения о свойствах оптимального решения позволяют указать более эффективный метод, заключающийся в последовательном удалении посредников из цепей платежей, то есть в перенаправлении ребер в графе неплатежей непосредственно от должников к кредиторам. На практике применение данного метода опирается на возможность реализации существенных полномочий управляющего органа по перенаправлению задолженностей предприятий, что ограничивает применимость метода, однако именно при этом возможно достичь максимального эффекта при реструктуризации задолженности. Используя описанные методы, в данной системе можно достичь снижения общего уровня задолженности более чем в два раза без затрат реальных средств. Согласно теореме остаток задолженности, имеющийся в системе после применения алгоритма отыскания кратчайшего пути на V1, не может быть ликвидирован путем реструктуризации задолженности. Для его ликвидации необходимо вкладывать в экономическую систему дополнительные средства. Рассмотрение методов распределения инвестиций между предприятиями экономической системы выполнено, например, в работе [3]. Список литературы 1. Гимади Э.Х., Глебов Н.И., Залюбовский В.В. О задачах целесообразного товарообмена. //Дискретный анализ и исследование операций. - 1998. - № 1. 2. Кристофидес Н. Теория графов. Алгоритмический подход. М.: - Мир, 1978. 3. Катулев А.Н., Колесник Г.В. Программный комплекс прогнозирования параметров экономической динамики региона. //Программные продукты и системы. – 1998. - № 2. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=931 |
Версия для печати Выпуск в формате PDF (1.58Мб) |
| Статья опубликована в выпуске журнала № 2 за 1999 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Интеллектуальная поддержка реинжиниринга конфигураций производственных систем
- Эволюционная модель формирования структур виртуальных предприятий
- Сравнительный анализ некоторых алгоритмов распознавания
- Сравнение сложных программных систем по критерию функциональной полноты
- К вопросу параметризации свойств программных средств обучения
Назад, к списку статей



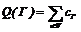 (v). (1)
(v). (1)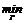 . (2)
. (2)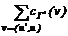 =
= =
=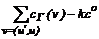 =deg–(u)|г – kco,
=deg–(u)|г – kco,

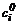 = min{cг(v) | " vÎ Li}.
= min{cг(v) | " vÎ Li}. .
. +
+ =
= =
= £ Q(Г),
£ Q(Г), и li ³ lo " Li.
и li ³ lo " Li.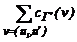 =
=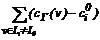 +
+ +
+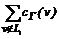 =
=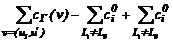 = deg–(u1)|г;
= deg–(u1)|г; L0\{v};
L0\{v};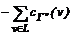 +
+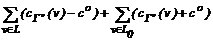 =
=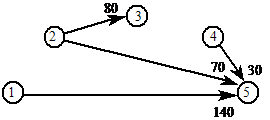
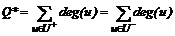 .
. .(6)
.(6) . (7)
. (7) ;
;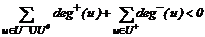 ,
, ;
; .
.