Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритмизация и программное обеспечение кинетических исследований сложных химически реагирующих систем
Аннотация:
Abstract:
| Авторы: Писаренко В.Н. () - , Жукова Т.Б. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 11682 |
Версия для печати Выпуск в формате PDF (1.60Мб) |
Целью кинетических исследований является установление механизма и кинетики химических реакций. Роль таких исследований исключительно велика, поскольку отсутствие кинетических моделей, адекватно отображающих динамику и статику химических превращений в широком диапазоне изменения технологических переменных, не позволяет проводить расчеты реакторных узлов и в конечном итоге является сдерживающим фактором при проектировании и оптимизации химических производств в целом. В работе рассмотрены основные этапы осуществления кинетических исследований, созданы комплексы алгоритмов и программ, необходимых на всех этапах решения кинетических задач. Все программы написаны на языках ФОРТРАН и ПАСКАЛЬ. При этом решение проблемы установления механизма сложной химической реакции и построение адекватной процессу кинетической модели осуществляется в следующей последовательности. 1. Формируется система гипотез о механизме протекания сложной химической реакции. Для каждого механизма реакции строится соответствующая ему кинетическая модель. 2. С использованием имеющейся априорной информации об изучаемой химической системе и с учетом выбранного критерия оптимальности строится стартовый план эксперимента. По результатам его реализации проводится оценка констант в кинетических моделях. 3. Оценки констант, полученных на втором этапе, уточняются с помощью методов последовательного планирования прецизионных экспериментов. 4. Дискриминация конкурирующих кинетических моделей с целью выбора одной, наиболее соответствующей результатам эксперимента. Предлагается следующий метод решения задачи первого этапа, которая формулируется следующим образом. Пусть известны (или постулируются из теоретических посылок, а также из физико-химических измерений) исходные реагенты, промежуточные соединения, продукты реакции, которые называются молекулярными видами Мib, i=1, ..., N. Требуется определить все возможные элементарные химические реакции Rr, r=1, ..., Q, происходящие среди N молекулярных видов, и построить системы гипотез о механизме протекания реакции. Для решения этой задачи представляем все молекулярные виды как целочисленные ассоциации структурных видов Мja, j=1, ..., N. В качестве структурных видов выбираем химические структуры, молекулы, атомы, радикалы, которые не претерпевают дальнейших расщеплений или перегруппировок в ходе рассматриваемых химических превращений. Следовательно, каждый химический вид Мjb, i=1, ..., N и каждая реакция Rr, r=1, ..., Q представимы следующим образом [1]. Мib= Rr = где aij – целые неотрицательные числа; bri – рациональные числа, называемые стехиометрическими коэффициентами. Вследствие необходимости выполнения каждой реагирующей системой закона сохранения масс или условий ее электронейтральности скалярное произведение векторов aj = (a1j, ..., anj)T, br = (br1, ..., brn)T должно быть равно нулю, то есть (aj * br) = 0, j=1, ..., M, r=1, ..., Q (3) в матричном виде ВА = 0, (4) где А={aij} – молекулярная матрица; В={bri} – матрица стехиометрических коэффициентов. Так как элементы молекулярной матрицы известны, то любая из возможных реакций может быть получена в результате решения однородной системы уравнений (4), которая называется основной системой уравнений (ОСУ). Справедливо и обратное утверждение – каждое решение ОСУ представляет собой возможную реакцию. Пусть ранг матрицы А равен Ua. Тогда максимальное число независимых реакций, которые могут протекать в рассматриваемой системе, равно Ub = N-Ua. Для вычисления стехиометрических коэффициентов bri, i=1, ..., N независимых реакций в молекулярной матрице найдем подматрицу А' ранга Ua и произведем соответствующую переиндексацию столбцов и строк матриц А и В так, чтобы индексы строк матрицы А изменялись от 1 до Ua включительно. Тогда уравнение (4) можно записать в виде
r=1,...,Ub, j=1,...,Ua . (5) При этом, если параметры bri выбрать следующим образом bri = dUa+r,i = { 0, если i ¹ Ua+r { 1, если i = Ua+r, (6) то каждое решение (5), (6) определит стехиометрически простую реакцию. На основе множества последних удается установить множество возможных элементарных реакций. Для нахождения всех стехиометрически простых реакций необходимо решить уравнения (5), (6) для каждой неособенной подматрицы А' ранга Ua. Естественно, что определенные таким путем стехиометрически простые реакции будут линейно зависимые. Тогда установление возможных механизмов реакции сводится к нахождению множества стехиометрических чисел {nr(p)}, удовлетворяющих (7), (8) и характеризующих некоторый механизм реакции.
где nr(p) – cтехиометрическое число r-й элементарной реакции по р-му маршруту, bs'(p) – cтехиометрический коэффициент s'-го вещества в р-м итоговом уравнении, I – число промежуточных веществ, Q – число стадий, К – число небоденштейновских веществ, входящих в итоговые уравнения маршрутов. Описанная выше процедура реализована в виде программы MECHANISM на языке ФОРТРАН-77. С использованием составленной программы были построены непротиворечивые имеющимся экспериментальным данным механизмы реакций этилирования ацетона в среде жидкого аммиака, синтеза метанола на цинкхромовых катализаторах, гидрирования масляных альдегидов на скелетных катализаторах, диспропорционирования толуола на цеолитных катализаторах. Для каждого синтезированного на ЭВМ механизма химической реакции строится соответствующая ему кинетическая модель, содержащая неизвестные кинетические константы. Последние оцениваются по экспериментальным данным, полученным в лабораторных безградиентных реакторах. Для оценки их численных значений необходима постановка небольшой серии стартовых опытов. Созданы алгоритмы и программы построения непрерывных и дискретных стартовых планов эксперимента STARTPLAN. Практическое использование стартовых планов эксперимента осуществляли при изучении кинетики каталитического гидрирования антрахинона и окисления антрагидрохинона. Оно оказалось исключительно эффективным и привело к сокращению в несколько раз общих затрат времени экспериментирования по сравнению с непланируемыми опытами. После реализации стартовых опытов по полученным значениям измерений необходимо вычислить точечные оценки параметров Q кинетических моделей. При этом использовали методы наименьших квадратов, максимального правдоподобия, байесовские, минимаксные [1-3]. Осуществляемый далее дисперсионный анализ конкурирующих моделей позволяет выявить в них статистически незначимые кинетические константы или их определенные комбинации. Затем проводится упрощение моделей, и для каждой из них устанавливается общее число констант, допускающих оценку. Последнее осуществлялось следующим образом. По информационной матрице М(e) определялись индивидуальные независимые константы, соответствующие некоторому неособенному минору М(e). При этом остальные индивидуальные константы задавались на основе априорной информации об их численных значениях. Конечно, численные значения, присваиваемые зависимым константам, не могут повлиять на предсказательную силу кинетической модели [3]. Разработаны алгоритм и программа установления идентифицируемости параметров модели IDENT на языках ФОРТРАН-77 и ПАСКАЛЬ 7.0. После получения точечных оценок независимых кинетических констант в моделях необходимо осуществить их проверку по статистическим критериям на соответствие экспериментальным данным. Основные способы проверки адекватности математических моделей базируются в основном на методах дисперсионного анализа и анализа остатков. К настоящему времени разработаны методы дисперсионного анализа и проверки адекватности однооткликовых моделей, и не существует до сих пор таковых для многооткликовых. Все же оказывается возможным для больших выборок применить для проведения дисперсионного анализа статистики V1 Бартлетта и Т4 Хагао [3, 4]. V1= T4 = 0.5{(n-pj) Sp + n2 Sp где S1 = А(Qj)/(n-pj) A(Qj)=åueu(Qj)eu(Qj)T – матрица остатков для j-й модели; å= Последние используются для проверки гипотезы Н о равенстве дисперсионно-ковариационных матриц å1 и å, то есть H: å1 = å. (11) Если гипотеза Н принимается, то тем самым утверждается адекватность модели результатам эксперимента. Бартлеттом и Хагао получены соответствующие аппроксимирующие выражения для функций распределения вероятностей статистик V1 и Т4, справедливые только для больших выборок. Однако такая ситуация все же редко имеет место на практике. Разработаны с привлечением метода статистического моделирования алгоритмы построения плотностей распределения V1 и Т4 для произвольных матриц å1 и å и для любых значений степеней свободы, что позволяет осуществлять дисперсионный анализ и проверку адекватности моделей при решении практически любых обратных кинетических задач. Для решения этих задач на языках ПАСКАЛЬ 7.0 и ФОРТРАН-77 созданы программы DPANAL и ADEQ. Определение точечных оценок максимального правдоподобия, байесовских и тому подобных еще не гарантирует того, что они получены с необходимой для исследователя точностью. Причем вся информация, характеризующая статистические свойства Q, сосредоточена в апостериорной плотности р(Q/y) или выборочной плотности распределения параметров р(Q). Однако построение точной выборочной плотности распределения возможно только для линейно параметризованных моделей, вместе с тем подавляющее большинство кинетических моделей (как и моделей физико-химических систем) нелинейно параметризованы. Линеаризация по Q нелинейных моделей не обеспечивает достаточно хорошей аппроксимации нелинейных моделей, даже репараметризованных, линеаризованными. Отсюда следует, что выборочная плотность распределения Q, соответствующая линеаризованной модели, будет существенно отличаться от р(Q), соответствующей нелинейной модели. Причем это расхождение, по крайней мере для небольших выборок, часто столь существенно, что может привести к получению абсурдных результатов. Предложен новый метод определения р(Q), свободный от указанных выше недостатков и не использующий в процессе принятия решения о численных значениях Q процедуру линеаризации исходной кинетической модели [3]. Рассмотрим кратко суть метода. Пусть в области экспериментирования G задана функция весов x(х), определяющая некоторый непрерывный нормированный план Dn со спектром e(х)=(x1, ..., xn). В результате реализации плана находится выборка конечного объема y1, ..., yn, где R – пространство исходов эксперимента. По выборке вычисляем оценки максимального правдоподобия. Последние, как известно, равны значениям, максимизирующим функцию правдоподобия L(y|Q). Моделируем затем на ЭВМ согласно плотности распределения ошибок измерений случайные векторы. Тогда гистограмма векторов, доставляющих максимум функции правдоподобия для выборок, моделируемых на ЭВМ, характеризует выборочную плотность распределения p(y|Q) параметров Q. Представим ее в виде разложения в ряд по полиномам Чебышева-Эрмита. p(Q)= *åå где w(Q-Q*) = exp(-1/2(Q-Q*)т å-1(Q-Q*)) – весовая функция, å – дисперсионно-ковариационная матрица оценок Q, вычисленная по линеаризованной кинетической модели. Отметим при этом, что для весовой функции w1(Q-Q*)= (2h)-p/2 çåç-1/2 w( Q-Q*) (13) cистема многочленов Чебышева-Эрмита {HM(Q-Q*), GL(Q-Q*)} обладает свойством биортогональности òw1(Q-Q*)GL(Q-Q*)HM(Q-Q*)dQ= =m1! ... mp!dl1m1 ... dlpmp, (14) где L=l1+...+lp, M=m1+...+Mp, dlm – символ Кронекера. Теперь выборочную плотность распределения р(Q) аппроксимируем отрезком ряда по многочленам Чебышева-Эрмита. Очевидно, что Р(Q) без потери общности можно представить в виде р(Q) = w(Q-Q*) p1(Q-Q*), (15) где w(Q-Q*) – нормальная плотность распределения, p1(Q-Q*) – некоторая непрерывная по Q функция. Так как w(Q-Q*) известна, то необходимо только использовать разложение в ряд p1(Q-Q*). Имеем р(Q-Q*)=S Из свойств многочленов {Gl(Q-Q*), Hm(Q-Q*)} следует, что наилучшее среднеквадратичное приближение при фиксированном L достигается, если неизвестные коэффициенты разложения Сm1... mp вычисляются по уравнениям Сm1 ... mp=òGm1 ... mp(Q-Q*)P(Q-Q*)dQ= =M{Gm1 ... mp(Q-Q*)}. (17) Cледовательно, расчет коэффициентов ряда Сm1 ... mp сводится к расчету с необходимой точностью интегралов (17). Для оценки их численных значений используется метод Монте-Карло, так как M{Gm1 ... mp(Q-Q*)}=1/N где N1 – объем выборки случайных векторов Qq, моделируемых на ЭВМ. Таким образом, получив на ЭВМ достаточно чисел Qq, определяем с необходимой точностью оценки интегралов (17) и отсюда погрешность аппроксимации Р(Q-Q*) усеченным рядом (16). Построенная на основании изложенного выборочная плотность распределения Р(Q) содержит в себе всю необходимую информацию о параметрах Q нелинейной кинетической модели, которую можно извлечь из выборки (y1, ..., yn) ограниченного объема при использовании выбранного метода оценивания. Она позволяет установить, обладают ли выбранные оценки параметров такими важными оптимальными свойствами, как несмещенность, эффективность, достаточность и робастность. По Р(Q) имеется возможность построить с высокой точностью доверительные интервалы и доверительные области, а также плотность распределения Р(h) прогноза динамического поведения химической системы по испытываемой конкурирующей модели. По Р(h) принимается решение о соответствии испытываемой модели реальному объекту. Так как при этом Р(h) получена с заданной точностью (без предварительной линеаризации модели) в виде разложения в ряд по ортогональным и биортогональным многочленам, то надежность принимаемых исследователем решений при этом резко возрастает. Отметим также, что использование Р(h) в процедуре дискриминации гипотез дает возможность сразу устранить многие недостатки, им присущие [6]. Как следует из вышеизложенного, предложенный метод построения плотностей распределения Q позволяет принципиально по-иному подойти к решению проблемы оценивания параметров в нелинейных моделях, ибо дает возможность осуществить поиск наилучшей в данной ситуации процедуры оценки параметров. При этом оценки параметров моделей должны удовлетворять необходимым требованиям точности для того, чтобы создаваемая кинетическая модель обладала достаточными прогнозирующими возможностями. Следовательно, требуется проведение дополнительного последовательно планируемого эксперимента для уточнения параметров. Процедура построения стратегии последовательного экспериментирования определяется конкретными задачами исследования на данном этапе. Среди них важнейшими являются: 1) оценка с заданной точностью параметра или подвектора параметров; 2) минимизация коэффициентов корреляции между двумя параметрами или группой параметров; 3) оценка вектора параметров в моделях. Для реализации подобных задач оказывается обычно достаточным проанализировать некоторые функционалы от информационной матрицы M(e), а также ее отдельные элементы или подматрицы. Для решения кинетических задач обычно используются критерии Д,Е,А–оптимальности. Проведенные исследования показали, что для сложных кинетических моделей не существует единого подхода к проведению прецизионного эксперимента и необходим подбор соответствующего критерия для каждой конкретной практической ситуации. Установлено при этом, что план эксперимента, оптимальный относительно одного выбранного критерия, обычно существенно неоптимален относительно других. Отсюда целесообразно характеризовать план эксперимента не одним, а совокупностью критериев. Часто выгодно поступиться оптимальностью плана по отношению к одному критерию, существенно улучшив при этом свойства плана относительно других. Следовательно, вместо использования частных желательно построить один комплексный критерий. В [6, 7] предложены такие критерии и показана их эффективность при решении обратных кинетических задач. Разработаны программы PRECISION на языке ФОРТРАН-77 для прецизионной оценки констант кинетических моделей. Обычно на заключительном этапе кинетического исследования несколько конкурирующих моделей соответствуют имеющимся экспериментальным данным, поэтому возникает задача их дискриминации. Существуют два основных метода дискриминации моделей – энтропийный и отношения вероятностей. Экспериментальная проверка энтропийного метода [3] показала, что последний является достаточно эффективным, по крайней мере по сравнению с классическим подходом, но не лишен, однако, существенных недостатков. Во-первых, метод не учитывает в процессе принятия решения предварительно поставленных "стартовых" экспериментов, хотя количество последних сравнимо с последующей серией дискриминирующих экспериментов. Во-вторых, принятие решения об окончании испытаний и об отбрасывании той или иной гипотезы базируется на единичных экспериментах, что снижает надежность полученных результатов из-за влияния на решение ошибок измерений. В-третьих, он применим только к линейным или предварительно линеаризованным кинетическим моделям. Последний недостаток устраняется при построении выборочных плотностей распределения Рj(Q) для каждой конкурирующей модели [3, 5, 6]. По Рj(Q), j=1, ..., m с использованием методов статистического моделирования определяем Рj(y/x) – плотность распределения предсказанного значения наблюдения в точке X при предположении справедливости j-й кинетической модели. Тогда информационные меры J(i:j), i, j=1, ..., m представимы в виде J(i:j)=òpi(y/x)ln[pi(y/x)/pj(y,x)]dy= =Mi[ ln[pi(y/x)/pj(y/x)], (19) где Мi – символ математического ожидания, индекс i указывает, что при вычислении математического ожидания предполагается справедливой i-я гипотеза. Образуем теперь скалярную дискриминантную функцию К(х). К(х)=РaT J(x) Pa, (20) где Pa = [p1, ..., pm]T, pl, l=1, ..., m – априорная вероятность принятия l-й гипотезы; J(x)=[Jij(x)], Jij(x)=J(i:j) – матрица относительного правдоподобия; х – условия проведения эксперимента; хÎG, G – область экспериментирования. Наивыгоднейшим считается тот эксперимент, например, N+1-й, который максимизирует К(х), то есть К(хn+1)=max Xn+1 EGK(xn+1). (21) Проводится эксперимент в Хn+1, и по его результатам оцениваются апостериорные вероятности Рjn+1, j=1, ..., m принятия конкурирующих кинетических гипотез. Дискриминирующие эксперименты по этой схеме проводятся до тех пор, пока одна из апостериорных вероятностей, например Рkn+1, не будет иметь значения, близкие к единице. Тогда принимается, что К-я модель наиболее соответствует экспериментальным данным. Если векторы наблюдений У и параметров Qj j=1, ..., m в моделях имеют большие размерности, то изложенная выше процедура непрактична, так как требует больших затрат времени счета на ЭВМ. Для этой ситуации предложен метод обобщенного отношения правдоподобия, который свободен от недостатков 1 и 2, присущих энтропийному методу. Мерой информации, используемой для дискриминации моделей, в данном случае является функция обобщенного отношения правдоподобия. Минимуму информации о системе кинетических гипотез соответствует равенство величин обобщенного отношения правдоподобия, а максимуму информации – максимальная разность между ними. Отсюда непосредственно следует, что для достижения в процессе принятия решения наиболее благоприятной информативной ситуации необходимо планировать эксперимент таким образом, чтобы от опыта к опыту максимизировать ожидаемый средний прирост суммы величины логарифма обобщенного отношения правдоподобия DL. DL(xn+1)= + × (S+Sj)(hn+1k-hn+1j) где Dj(N) – ковариационная матрица оценок констант j-й модели, вычисленная по N опытам; Lj(N) – обобщенная функция правдоподобия. Lj(N)= ×exp *(yrsj-hrsj) uj(N)= Lj(N)/(Пk=1mLk(N))1/m, sj = x(j) Dj(N) x(j)T, (23) где х(j) – матрица размерности n=pj с общим (rj) – элементом вида xri(j)=drrN+1(j)/dQi(j); индексы j, i, r характеризуют соответственно номера модели, параметра и отклика. После выполнения N+1-го опыта вычисляется величина обобщенного отношения правдоподобия uj(N+1), которая затем сравнивается с останавливающей границей Аj. Aj=(1-ejj)/ где еjq – определяет вероятность принятия j-й гипотезы. Количество гипотез сокращается на единицу, и формируется новое обобщенное отношение правдоподобия. Таким образом, число гипотез в ходе экспериментирования будет последовательно уменьшаться до тех пор, пока не останется одна, которая и будет принята. Изложенные выше процедуры дискриминации конкурирующих моделей реализованы в виде программ на языке ФОРТРАН-77 DISCRIM и DISCRIM2. Разработанные программы использовались, в частности, при изучении кинетики реакции гидрирования этилена и этилирования ацетона в среде жидкого аммиака. Они показали себя более эффективными по сравнению с энтропийным методом и для получения одних и тех же конечных результатов при принятии решения о кинетической модели (наиболее соответствующей экспериментальным данным) потребовали постановки меньшего числа дискриминирующих опытов. При этом следует иметь в виду, что использование разработанных методов приводит к увеличению надежности проводимых кинетических исследований. В заключение отметим также, что применимость различных процедур дискриминации моделей не ограничивается областью кинетических исследований. Последние с неменьшим успехом могут быть распространены на все области химико-технологических исследований, связанных с изучением механизмов физико-химических процессов и построением их математических моделей. Таким образом, разработан пакет прикладных программ CHEMKINETICS, который позволяет существенно упростить и ускорить построение кинетических моделей по непланируемым и последовательно планируемым экспериментам при одновременном увеличении надежности результатов кинетических исследований. Список литературы 1. Писаренко В.Н., Погорелов А.Г. Планирование кинетических исследований. - М.: Наука, 1969. - 175 с. 2. Кафаров В.В., Писаренко В.Н. // Успехи химии. - 1980. - Т. 49 - С. 193-222. 3. Писаренко В.Н. Итоги науки и техники. Процессы и аппараты химической технологии. - М.: ВИНИТИ, 1981. - Т.9. - С. 3-86. 4. Hagao H. // Ann. Stat., 1973 - v. 1 - P. 400-405 5. Писаренко В.Н., Жукова Т.Б. // Тр. МХТИ: Математическое обеспечение систем оптимизации, проектирования и управления ХТП. - 1986. - Т. 140. - С. 50-62. 6. Кафаров В.В., Писаренко В.Н., Жукова Т.Б. // Тр. II конф. по кинетике каталитических реакций. - Новосибирск: СоАН СССР. - 1975. - С. 18 - 27. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=972 |
Версия для печати Выпуск в формате PDF (1.60Мб) |
| Статья опубликована в выпуске журнала № 1 за 1998 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Место XML-технологий в среде современных информационных технологий
- Программные средства автоматизации приборостроительного производства изделий радиоэлектронной аппаратуры
- Оптимизация структуры базы данных информационной системы ПАТЕНТ
- Автоматизированная система принятия решений при стратегическом планировании устойчивого развития региона в условиях нечеткой информации
- Алгоритмы и программное обеспечение системы обработки топопланов
Назад, к списку статей



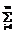 aij Mja, i=1, ..., N, (1)
aij Mja, i=1, ..., N, (1) bri Mib, r=1, ..., Q, (2)
bri Mib, r=1, ..., Q, (2)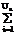 bri*aij= -
bri*aij= -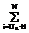 bri*aij,
bri*aij,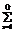 brsnr(p)= 0, s=1,...,I, (7)
brsnr(p)= 0, s=1,...,I, (7) , (9)
, (9) S1
S1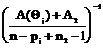 - I
- I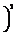 +
+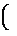 S
S - I
- I }, (10)
}, (10) (yu- y1)(yu-y1)T/(n2-1)=A2/(n2-1), y1, y2, ..., yn2 – повторная выборка объема n2; y1=
(yu- y1)(yu-y1)T/(n2-1)=A2/(n2-1), y1, y2, ..., yn2 – повторная выборка объема n2; y1= * w (Q-Q*) *
* w (Q-Q*) * Ha1...ap (Q - Q*), (12)
Ha1...ap (Q - Q*), (12)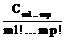 Нm1... mp(Q-Q*). (16)
Нm1... mp(Q-Q*). (16) G(Q1-Q*), (18)
G(Q1-Q*), (18) Sp(S+Sj) (S+Sk)-1 - mSpJ +
Sp(S+Sj) (S+Sk)-1 - mSpJ + ×
×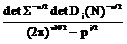 ×
× -1/2
-1/2 srsS(yrl-hrlj)*
srsS(yrl-hrlj)* S-1={srs},
S-1={srs}, (1-еjq)1/m, j=1, ..., m, (24)
(1-еjq)1/m, j=1, ..., m, (24)