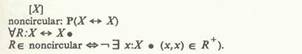Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: () - , () - | |
| Ключевое слово: |
|
| Page views: 16759 |
Print version |
Обычно полная спецификация модели данных состоит из неформального текстуального описания наряду с формальной спецификацией. Неформальное текстуальное описание предоставляет краткую характеристику модели и выделяет ее основные показатели. Формальная спецификация дает полное и точное определение семантики и основу для реализации модели. Полуформальная же находится между двумя видами спецификации. Она можег описывать только некоторые аспекты модели, например структуру, а не поведение, и при этом сопровождать их пояснительным текстом.
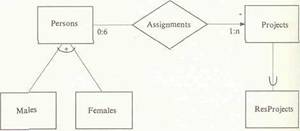
Преимущества графического описания структуры предметной области очевидны [I]. Оно эффективно при документировании, так как дает возможность читателю понять сущность структуры системы и более быстро постичь подробности спецификации. К тому же оно является важным этапом в процессе проектирования, предоставляя абстрактную схему системы, которая затем в процессе уточнения становится подробной формальной спецификацией. Следовательно, производится первоначальное структурирование спецификации. Это можно связать с использованием моделей типа "объект-отношение" в проектировании базы данных. Модель этого типа идентифицирует интересующие нас объекты в предметной области и взаимосвязи между ними. Полученную при этом схему "объект-отношение" можно затем преобразовать в эквивалентную схему реляционной базы данных, которая может подвергаться последующим преобразованиям в вид, удобный для реализации. Модель "объект-отношение" играет важную роль в создании структуры реляционной схемы, которая затем расширяется за счет детализации в процессе реализации и эксплуатации. Модель такого типа является существенной частью документирования системы. Также полагаем, что концепции моделиролншя данных могут играть важную роль и в предоставлении промежуточной, полуформальной спецификации любой прикладной системы, и в определении первоначальной структуры формальной спецификации этой системы. В статье обсуждается использование описания модели данных в собственных терминах как промежуточного уровня спецификации. Такое мета-циклическое описание очень ценно при документировании модели и является основой для структурирования формальной спецификации. Целесообразно использование метациклического описания для тестирования возможностей моделирования модели данных. Метациклическое описание можно использовать для разработки системы базы данных, которая поддерживает унифицированную обработку метаданных и данных. Следовательно, устройства просмотра и процессоры обработки, запросов можно применять для выборки информации и данных схемы. В данной статье использована объектно-ориентированная модель данных, в которую введено понятие отношений, чтобы обеспечить поддержку для прямого представления взаимосвязей между объектами. Оказывается, что эти взаимосвязи обеспечивают основу для начального структурирования формальной спецификации на языке Z [4]. Модель данных BROOM (объектно-ориентированная модель бинарных отношений) разработана в рамках проекта Comandos [5], который является проектом Esprit. Он связан с созданием и управлением открытых распределенных систем. Услуги по управлению данными системы Comandos предоставляются через библиотеку общих типов совокупностей, которые поддерживают модель BROOM [6]. ОБЗОР МОДЕЛИ ДАННЫХ BROOM В настоящее время большое распространение получили четыре вида модели данных: реляционная модель данных, модели типа "объект-отношение", семантические и объектно-ориентированные модели. Широкое распространение реляционной модели определяется в первую очередь ее простотой, однородностью, наличием языков-запросов высокого уровня, что стало возможным благодаря введению общего типа совокупности данных - отношения. Основой языков запросов высокого уровня стала алгебра операций над этими совокупностями (в противоположность операциям над индивидуальными записями данных, которые лежат в основе сетевых и иерархических моделей данных). В то же время стали использоваться модели типа "объект-отношение11 в моделировании данных высокого уровня прикладных программ; первоначально предполагалось их использование для проектирования баз данных. Семантические модели данных [7] можно рассматривать как разработки моделей типа "объект-отношение", которые поддерживают структуры классификации, основанные на отношениях ISA между наборами объектов. Прослеживается тенденция к использованию объектно-ориентированных моделей. С их помощью можно моделировать как динамические, так и статические свойства данных, которые охватывают семьн- тику высокого уровня прикладных программ. Многие поэтому считают, что объектно-ориентированные модели превосходят семантические, а также модели типа "объект-отношение". Однако большим недостатком объектно-ориентированных моделей считается невозможность прямого представления отношений [8]. При проектировании больших систем оказалось, что отношения являются наиболее эффективным механизмом абстракции при разбиении систем на подсистемы. В статье показано их использование для структурирования спецификации на языке Z. В последнее время внесены предложения о расширении объектно-ориентированных моделей для поддержки отношений как объектов класса "первые значения" [6, 8-13]. Хотя и были некоторые предложения об использовании алгебраических операций над совокупностями объектов [14], но все же некоторые системы, используя по одному объекту во время обработки, потеряли ряд преимуществ реляционной модели в функции обработки запросов высокого уровня. Модель данных BROOM объединяет все лучшие характеристики этих видов моделей: объектно-ориентированную модель с различными видами совокупностей (наборы, последовательности или мультимножества); прямую поддержку при представлении отношений; разнообразные классификационные структуры; алгебру множеств. В модели BROOM объекты классифицируются по числу членов в унарной совокупности. Унарная совокупность - это группировка идентификаторов объекта. Она имеет свойства набора, мультимножества или последовательности в зависимости от возможности наличия дубликатов и обеспечивает специфицированную упорядоченность ее элементов. Вид унарной совокупности и тип ее членов указываются при объявлении типа, связанного с этой совокупностью. Например, заданное объявление типа совокупности PersonSet будет следующего вида: type PersonSet = se( [person]. Тогда в совокупности Persons (физические лица) типа PersonSet, элементы совокупности Persons должны быть типа Persons, и совокупность Persons будет иметь свойства набора, т.е. элементы ее неупо-рядочены И в ней нет дубликатов. Заметим, что тип совокупности может включать любое количество экземпляров. Отношения между объектами представляются посредством бинарных совокупностей (группировок пар идентификаторов объекта). Двоичная совокупность будет включать ассоциированные объектные и исходные совокупности, к которым принадлежат соответственно первый и второй элемент пары. Двоичные совокупности имеют те же самые свойства набора, мультимножества и последовательности, что и унарные совокупности. Например, объявление типа совокупности будет иметь вид: type AssignmenlSeq. = seq [person, project]. В этом случае экземпляр Assignments (присваивания) типа AssignmentSeq, будет бинарной совокупностью, каждый член которой будет состоять из пары идентификаторов объекта. Так как объявленный вид совокупности Seq, то произойдет обязательное упорядочивание пар, которое будет выполняться на основе вставок до тех пор, пока не будет указан другой вид упорядочивания. Ясно, что существуют некоторые ограничения на идентификаторы объекта, которые могут появляться в парах элементов Assignments. При объявлении типа указывается, что первый элемент пары должен быть типа person (физическое лй1|0), а второй — типа project (проект). Далее, любой экземпляр бинарной совокупности будет отражать взаимосвязи между членами двух конкретных совокупностей. Следовательно, если бинарная совокупность включает пару (х, у), то х должен принадлежать указанной исходной совокупности, а у - специфицированной объектной совокупности. Например, предположим, что Projects является унарной совокупностью объектов "проектов", то можно специфицировать исходную совокупность Assignments как Persons, а объектной совокупностью будет Projects. На рисунке 1 это представлено графически.
Рис. I. Пример модели BROOM Здесь унарные совокупности представлены в виде заштрихованных прямоугольников, а бинарные совокупности в виде заштрихованного ромба. Для указания свойств набора, последовательности или мультимножества в совокупности используются различные виды штриховки. "Точечная" штриховка указывает свойства набора, "линейная" - свойства последовательности, "решетка" — особенности мультимножества. Произвольно тип элементов члена совокупности можно записать непосредственно с символом совокупности. Дуги, соединяющие двоичную совокупность с ее исходной и объектной совокупностями, помечаются ограничителями числа элементов. Направленная дуга указывает, какая совокупность является объектной. Ограничение '0:6' в исходной совокупности Persons указывает, что каждый элемент совокупности Persons можно присвоить шести элементам совокупности Projects. Ограничитель '1:1' в объектной совокупности Progects указывает, что каждый член множества Projects должен присваиваться хотя бы одному элементу множества Persons. Пример, представленный на рисунке 1, также иллюстрирует виды классификационных структур, которые поддерживаются в модели. Совокупность Projects включает подсовокупность ResProjects, a совокупность Persons - две подсовокупности Males (мужчины) и Females (женщины). Знак ' + ' указывает, что две подсовокупности формируют покрытие Persons, т.е. что каждый член совокупности Persons должен принадлежать хотя бы одной из совокупное-
тсй Males или Females. Знак ' ' указывает, что две подсовокупности являются непересекающимися, т.е. ни один объект совокупности Person не может одновременно быть членом совокупности Males и Females. Если члены набора подсовокупностей взаимно непересекающиеся, то они образуют сегмент порождающей совокупности; а при формировании покрытия и сегмента получается точный сегмент порождающей совокупности. Такие структуры классификации можно применять в любых совокупностях; следовательно, в наборе подсовокупностей возможно иметь сегмент бинарной совокупности. Следует заметить, что у совокупности может быть несколько структур классификации. Таким образом, унарные совокупности являются группировкой объектов, а элементы унарной совокупности являются идентификаторами объектов. Фактически же унарные совокупности могут включать любые виды значений в качестве элементов (в соответствии с объявлением типа), где значения могут быть идентификаторами объектов, записями или базовыми величинами, т.е. представляться в виде целых чисел. Соответственно и пары значений любого вида могут быть элементами бинарной совокупности. Следует отметить, что бинарная совокупность не является эквивалентом унарной совокупности представления записи. Любая из бинарной совокупности может быть исходной и объектной. Следовательно, возможно использовать двоичную совокупность, которая устаЕсавливаст отношения между бинарной и унарной. Подобные обобщения позволяют моделировать п-арные отношения и атрибуты отношений. Алгебра множеств (AQL) связана с моделью BROOM. Алгебраические операции можно рассматривать как обобщения операций реляционной алгебры для видов совокупностей, поддерживаемых в системе BROOM. Есть операции для поддержки преобразований различных видов совокупностей. В данной статье рассматривается только структурная часть модели BROOM, поэтому не обсуждаются проблемы алгебры множеств. МЕТАЦИКЛИЧЕСКОЕ ОПИСАНИЕ МОДЕЛИ BROOM После выявления общих характеристик модели BROOM строится ее метациклическое описание. Основное внимание на промежуточном уровне спецификации уделяется 'сгрукхурной части модели. Перед началом процесса уточнения понятий алгебры множеств необходимо точно установить виды совокупностей, которые будут поддерживаться моделью BROOM. Совокупность - это объект, который является группировкой значений, и сам по себе значение. Следует подчеркнуть, что термин "значение" здесь относится как к объектам, так и к необъектам. На рисунке 2 представлено графическое описание структур совокупностей модели BROOM. Значением может быть пара, состоящая из Значений .первою и второго элемента, или же элементарная величина. Каждая совокупность является объектом, что указывается посредством дуги между объектами (Objects) и совокупностями (Collections). Существует два вида классификации совокупностей: 1) наборы, последовательности и мультимножества и 2) унарные и бинарные совокупности. Следовательно, каждая совокупность имеет свойства обоих видов классификации. Каждый элемент бинарной совокупности связан с объектной и исходной совокупностью. Бинарная совокупность "члены" (Members) отражает связь между совокупностью и ее элементами. Заметим, что совокупность "члены" ограничивается определенным сегментом в совокупности "бинарные члены" (Binary Members), который связЕ^вает совокупность "бинарные совокупности" (Binary Collections) и совокупность "значения пар" (Pair Values), и в совокупности "унарные члены", связывающий "унарные совокупности" и "элементарные величины". Значения в модели BROOM ассоциируются с одним или с несколькими типами. Например, целочисленное значение является типом "целые числа" (INTEGER). Значение объекта, которое является экземпляром типа "мужчины" (Masculines), будет экземпляром супертипов, относящихся к типу "мужчины". В модели BROOM все типы, в том числе и типы совокупностей, могут включать любое количество экземпляров. Следовательно, отношения между типами и значениями будут вида "многие-ко-многим".
Бинарная совокупность "экземпляры" детализируется относительно структуры, чтобы обеспечить непротиворечивость между формой типа и его значением. Например, элементарная величина может быть и экземпляром совокупности "типы элементарных величин", а унарная совокупность наборов может быть только экземпляром совокупности "типы унарных совокупностей наборов". На рисунке 3 представлена только часть структуры.
Структуры классификации BROOM представлены на рисунке 4. Между членами совокупностей существуют связи подсовокупностей типа "многие-ко-многим". Заметим, что подсовокупности (Sub-Colleetions) должны быть частично упорядоченными, т.е. иметь следующие свойства: а) если се совокупности, то (с,с)е подсовокупности (рефлексивные); б) если (х,у)еподсовокупности и (у,х)еподсовокуп- ности, то х=у (асимметричные);
в) если (_х,у)еподсовокупности и Су,г)еподсовокуп- ности, то (х,г)еподсовокупности (транзитивные).не является обязательным непересечение исходных и объективных совокупностей, т.е. типы элементов исходной и объектной совокупностей имеют общий супертип. Можно маркировать однородную бинарную совокупность с помощью следующих характеристик: = рефлексивная э^ нерефлексивная ■ эквивалентность < частичная упорядоченность < полная упорядоченность < нерефлексивное, транзитивное замыкание. Последняя характеристика указывает, что однородная бинарная совокупность является кецикличной. Заметим, что некоторые из этих характеристик можно рассматривать как ограничения, которые необходимо проверить при вставке элементов, в то время как другие можно рассматривать как вид производной информации. Например, если бинарная совокупность рефлексивная, то нет необходимости запоминать такие вводы данных, как (х, z) в данной совокупности. Элемент совокупности "семьи" (Families) представляет собой набор совокупностей, который формирует сегмент или покрытие какой-то другой совокупности. Каждый член совокупности "семьи" дол-жев[ являться членом сегментов (Partitions) или покрытий (Covers), а возможно, и членом обеих этих совокупностей. Каждая семья совокупности включает совокупность "родители" и одну или несколько совокупностей "ребенок". Совокупность "дети" формирует сегмент и/или покрытие совокупности "родитель", и следовательно каждая совокупность "ребенок" должна быть подсовокупностью совокупности "родитель". Схема дополнена прямоугольником, что специфицирует это ограничение; инверсия совокупности "дети" вместе с совокупностями "родители" содержится в подсовокупностях. Заметим, что совокупность может быть "ребенком" многих совокупностей "семьи". Скорее всего бинарная совокупность "дети" (Children) является последовательностью, а не набором при индексировании подсовокупностей. Это условие необходимо при определении соответствующих подсовокупностей в связанных и эом орфических структурах без явного объявления. Создание метациклического описания модели BROOM — итеративный процесс в том смысле, что необходимы постоянные изменения первоначальных концепций. Подобные метациклические описания необходимы при тестировании моделирующих возможностей модели, т.к. при этом создается очень сложная "предметная область" и предоставляется возможность тестировать модель в различных прикладных программах, а не только на стандартных примерах базы данных. СПЕЦИФИКАЦИЯ МОДЕЛИ BROOM НА ЯЗЫКЕ Z Здесь описываются общие принципы преобразования описания модели BROOM в спецификацию на языке Z. Методология преобразования иллюстрируется на рисунке 2 описанием структуры "значения". Прежде всего введем конструкцию языка Z для каждой базовой концепции модели BROOM, такой как формы совокупностей и структурные ограничения в совокупностях. Эти концепции могут вводиться в виде базовой конструкции языка Z или же общей константы. Унарные совокупности наборов, последовательностей и мультимножеств и бинарные совокупности наборов можно соответственно представить наборами, последовательностями, мультимножествами и отношениями языка Z. С помошъю функций языка Z можно представить бинарную совокупность набора с ограничением числа элементов, которое указывает, что отношение должно быть функциональным. Общие константы можно использовать для спецификации сегментов, покрытий и неиикличиых, однородных, бинарных совокупностей. Общие константы понятий, непересечений и сегментов относительно последовательностей наборов, представленные на рисунке 2, включается, как часть Z [4]. Однако следует заметить, что обычный сегмент спецификации на языке Z точно соответствует нашему сегменту, так как он специфицирует то, что последовательность наборов должна быть не только непересечением, но и покрытием порождающего набора. Поэтому опишем общие константы покрытий и сегментов следующим образом: И. У] _covers_, _partitions_, _srtictlypartitions_: (/-+*РЛ") ** PX VS:/-t+PX;T:PX • (S covers T ■*» U{rt;domS • Sn} = 7) Л (S partitions T <* disjoint S Л U[n:domS • Sn}C Г) Л (S strictlypartitions T *> S covers T A S partitions 7) Дополнительно необходимо описать общие константы свойств однородных бинарных совокупностей о которых упоминалось в предыдущем разделе, т.е рефлексивных, нециклических свойств. Можно, например, специфицировать набор нециклических отношений следующим образом.
Общий подход, принятый к преобразованию описания модели BROOM в спецификацию на языке Z, заключается в том, чтобы создать спецификацию Z для каждой структуры классификации и затем объединить их в спецификацию всего полного описания модели BROOM. Обычно структура классификации является ацикличным направленным графам, КОТО' рый описывает совокупность и вес ее подсовокупности. Определяется схема Z для каждой семьи совокупности в структуре классификации, а затем объединяет их в схему полной структуры классификации. Отметим, что существует два вида бинарных совокупностей: однородные, т.е. они связывают совокупность или же саму с собой, или же с одной из своих Подсовокупностей, и те, которые связывают совокупности, принадлежащие к различным структурам классификации. Данный метод станет более понятным, если создать спецификацию Z структуры, представленную на рисунке 2. При обсуждении структуры (рис. 2) ничего не упоминалось о типах использованных совокупностей: Например, какого же типа члены совокупности объекты (Objects)? Здесь объект отождествили с идентификатором этого объекта, и следовательно объекты являются набором идентификаторов объекта. Поэтому и ввели базовое описание типа OBJID, которое и является набором всех идентификаторов объекта. [OBJID] Затем можно определить схему совокупности "семья", которая классифицирует совокупность как набор, последовательность или мультимножество. COLLECTION KINDS Collections, Sets, Sequences, Bags: P OBJID {Sets, Sequences, Bags) strictlypartitions Collections Теперь представим схему COLLECTIONFORMS (формы совокупности) для круглого вида классификации совокупностей в одну из бинарных или унарных форм. COLLECTIONFORMS Collections, Unary Collections, Binary Collections: P OBJID Sourse, Targets: OBJID -* OBJID dom Sources = Binary Collections ran Sources = collections Sources e noncircular [OBJID] dom Targets = Binary Collections ran Targets = collections Targets e noncircular [OBJID] {UnaryCollections, BinaryCotlections} strictlypartitions Collections Заметим, что бинарные совокупности Sources (источники) и Targets (объекты) объявляются как полные функции. Вообще же ограничения на число элементов в бинарных совокупностях могут специфицировать отношение как частичную функцию, полную функцию или как подчиненную функцию. Все это отражается в ассоциативной схеме. Две эти схемы можно объединить в схему COLLECTIONS следующим образом: COLLECTIONS = COLLECT1ONKINDS Л COLLECTIONFORMS При дальнейшей разработке структуры классификации значений необходимо ввести схему OBJECTS следующим образом: OBJECTS COLLECTIONS Objects: P OBJID Collections C Objects До сих пор рассматривались совокупности с типом элемента OBJID. Другими определениями типов, необходимых для спецификации значений, является набор всех символов STRING и заданный набор всех целых чисел Z. [STRING^ Все другие оставшиеся унарные совокупности, представленные на рисунке 2, состоят из членов раз- личного типа. Ими могут быть символьные строки, целые числа, идентификаторы объектов или пары значений. Все эти наборы значений будут непересекающимися. Для соответствия с совокупностями (рис. 2) здесь вводятся следующие типы объединения. BASEVALUE == STRINCAJZ ATOMICVALUE = = BASEVALUEUOBJID VALUE = = ATOMJCVALUEUVALUEx VALUE Теперь можно ввести схему совокупности "значения", которая включает спецификацию бинарной совокупности "члены". Элементами совокупности "члены" являются пары элементов: первый элемент идентификатора объектов (OBJID) и второй элемент значение (VALUE). Members, BinaryMembers и UnaryMembers вводятся как однородные отношения в наборе VALUE. VALUES COLLECTIONS Values; P VALUE Members, Unary Members, BinaryMembers: VALUE ** VALUE dom Members С Collections ran Members С Values Members enoncircularf VA L UE\ dom UnaiyMemberstZUnaryCollections ran UnaryMembersQ ATOMICVALUE dom UnaryMembersCLBinaiyCollections ran BinaryMembersT\ATOMICVALUE= 0 { UnaryМетпЬеп, BinnrvMembeuJstrictlypartitions Members Предикативная часть ограничивает домен Members типом значения OBJID, который принадлежит набору Collections. Домены и диапазоны отношений UnaryMembers и BinaryMembers ограничиваются соответствующими наборами значений. Совокупность Members специфицируется как нецикличное отношение VALUE, это гарантирует, что ни одна из совокупностей не является членом самой этой совокупности. Специфицировав описание модели BROOM (рис. 2), в схеме VALUES можно точно таким же образом специфицировать описание структуры типа модели BROOM в схеме TYPES (типы). Совокупность "типы" является набором имен, поэтому введем другое, базовое определение типа NAME, которое является набором всех имен. [NAME] Имея уже схемы VALUES и TYPES, можно создать схему INSTANCES (экземпляры), которая определяет бинарную совокупность "экземпляры" и включает VALUES и TYPES. INSTANCES VALUES TYPES Instances: NAME «-> VALUE dom Instances С Types ran Instances^ Values Все изложенное преднаэначенно для описания общего подхода к преобразованию описания модели BROOM в схеме Z. Можно более эффективно использовать обобщение, чтобы специфицировать часто встречающиеся структуры независимо от того, являются ли они структурами модели BROOM или же изоморфическими структурами в описании BROOM. Специфицировав структурную часть модели BROOM, можно специфицировать операции алгебры множеств. Список литературы 1. Reynolds J.C. Definitional Interpreters for Higher-Order Programming Languages, In Proceedings of the ACM Conference, 1972. 2. Chen P.P. The entity-relationship model: Toward a unified view of data, ACM Transactions of Database Systems, Vol. 1, No. 1, pp 9-36, 1976. 3. Howe D.R. Data Analysis for Data Base Design, pub. Edward Arnold, 1983. 4. Spivey J.M. The Z Notation, pub. Prentice Hall, 1989. 5. Comandos Consortium, The Comandos Guide, Esprit Project 2071, 1991. 6. Harper D.J. and Nome M.C. Data Management for Object- Oriented Systems, In Aspects of Databases, pub. Butterworlh- Hememann, 1991. 7. Hull R. and King R. Semantic Data Modelling: Survey, Applications and Research Issues, ACM Computing Surveys, Vol. 19, No. 3, pp 201-260, 1987. 8. Rumbaugh J. Relations as Semantic Constructs in an Object- Oriented Language, In Proceedings OOPSLA 1987, pp 466-481, 1987. 9. Albano A. Ghelli G. and Orsini R. A Relationship Mechanism for A Strongly Typed Object-Oriented Database Programming Language, to appear In Proceedings of VLDB 91, 1991. 10. Bratsberg S.E. FOOD: Supporting explicit relations in a Fully Object-Oriented Database, In Proceedings IFIP TC2 Conference on Object Oriented Databases, Windermere, U.K., 1990. 11. Diaz O. and Gray P.M.D. Semantic-rich User-defined Relationship as a Main Constructor In Object Oriented Databases, In Proceedings IFIP TC2 Conference on Object Oriented Databases, Windermere, U.K., 1990. 12. Harder Т., Меуег-Wegener K., Mitschang B. and Sikeler A. Prima - a DBMS Prototype Supporting Engineering Applications, In Proceedings 13th" VLDB Conference, Brighton, U.K., 1987. 13. Nassif R., Qtu Y. and Zhu J. Extending the Object-Oriented Paradigm to Support Relationships and Constraints, In Proceedings IFIP TC2 Conference on Object-Oriented Databases, Windermere, U.K., 1990. 14. Cluet S-, Delobel C, Lecluse С and Richard P. RELOOP, во algebra based query language for an object-oriented database system, Data and Knowledge Engineering, S, pp 333-352, 1990. 15. Booth G. Object Oriented Design with Applications, pub. Benjamin/CummingJ, 1991. |
| Permanent link: http://swsys.ru/index.php?id=1444&lang=en&page=article |
Print version |
| The article was published in issue no. № 2, 1992 |
Perhaps, you might be interested in the following articles of similar topics:
- Расчет нечеткого сбалансированного показателя в задачах взвешивания терминов электронных документов
- Комплекс автоматизированного проектирования геотехнических сооружений "КАППА"
- Автоматизированное рабочее место расчета стоимости эксплуатации кораблей
- Механизм контроля качества программного обеспечения оптико-электронных систем контроля
- Унифицированный информационный интерфейс и его реализация в комплексной САПР
Back to the list of articles