Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: () - , () - | |
| Keywords: , correctness, |
|
| Page views: 8950 |
Print version Full issue in PDF (2.59Mb) |
Рассмотрим задачу верификации корректности выражения в языке программирования Хаскел с точки зрения правильности использования некоторой функции. Здесь под правильным использованием понимается применение функции лишь к аргументам, удовлетворяющим определенному предикату P-логики. Данная задача состоит в том, чтобы удостовериться, что в процессе вычисления выражения эта функция не будет применена к неправильным аргументам. Частным случаем здесь является полный запрет на вызов определенной функции. Например, для кода, полученного из ненадежного источника, может потребоваться гарантия того, что в нем не вызывается функция завершения программы. Предикат P-логики, соответствующий данному частному случаю, будет просто тождественно ложен. Рассмотрим такой простой пример, как насыщенное применение функции к аргументам
где через Поясним это на примере следующих Хаскел-определений:
Пусть функция Однако можно видеть, что значение функции f зависит от ее второго аргумента ( Необходимо привести некоторые соображения, чтобы обосновать справедливость приведенных рассуждений. Многие, посмотрев на выражение Однако стоит еще раз подчеркнуть, что Хаскел обладает нестрогой семантикой, а способ ее реализации спецификацией языка никак не навязывается. Помимо ленивого вычисления, было также предложено оптимистичное вычисление [3], которое может иногда вычислять подвыражения до того, как их значения фактически понадобятся. Тем не менее приведенные выше соображения корректны вне зависимости от механизма вычисления выражений. Дело в том, что Хаскел – безопасный язык. Система типов уже гарантирует, что программа не завершится с критической ошибкой. Таким образом, не важно, будет ли фактически вызвана функция с неправильными аргументами, главное – то, чтобы значение верифицируемого выражения не зависело от результата этого неправильного применения. Для того чтобы формулировать более слабые утверждения корректности аргументов функции, построим шаблон высказывания на основе определения данной функции. После этого в полученный шаблон подставляются выражения аргументов и их собственные утверждения корректности. Таким образом учитывается структура функции. Данный шаблон будет содержать в себе потенциал для получения более слабого утверждения. Это можно описать следующим образом: пусть
То есть высказывание Задача сводится к определению функции В приведенном примере с функциями Несколько упрощая задачу, а именно, не рассматривая рекурсию и функции высшего порядка, достаточно определить Самое существенное здесь – условные выражения, поскольку они являются прямым показателем зависимости результата от входных данных. Операционно это выражается в том, что исследуемое выражение вычисляется тогда, когда нужно вычислить значение всего условного выражения: Здесь для построения шаблона высказывания мы рекурсивно используем В правой части выражение Для выражения, представляющего собой применение функции к аргументам, нужно опять решить ту самую задачу, которая ставится в данной работе. Очевидно,
Для всех остальных выражений T(e) можно определить как
Здесь И, наконец, выражению, представляющему собой просто переменную Такого тривиального определения функции При решении задачи определения корректности программы с точки зрения правильности использования определенных функций можно получать различные утверждения логики. Все они будут верными в том смысле, что их истинность соответствует корректности программы. Однако при тривиальном подходе получаемые утверждения в большинстве случаев слишком сильны. Следовательно, во-первых, их сложнее доказывать и, во-вторых, большее множество программ будет признано некорректными. Предложенная мето- дика позволяет получать более слабые утверждения корректности программ. Таким образом, корректность становится легче доказуемой, и мно- жество доказуемо корректных программ лучше аппроксимирует множество действительно корректных. Список литературы 1. Peyton Jones S. и др. Report on the programming language Haskell 98, a non-strict, purely functional language, http://haskell.org, 1999. 2. Augustsson L. Compiling lazy functional languages, part II, Chalmers University, 1987. 3. Ennals R., Peyton Jones S. Optimistic evaluation: an adaptive evaluation strategy for non-strict programs, International Conference on Functional Programming, 2003. |
| Permanent link: http://swsys.ru/index.php?id=1595&lang=en&page=article |
Print version Full issue in PDF (2.59Mb) |
| The article was published in issue no. № 3, 2008 | |
| Статья находится в категориях: Haskell | |
| Статья относится к отраслям: Вычисления | |
Perhaps, you might be interested in the following articles of similar topics:
 (в Хаскеле применение функции записывается без скобок). Помимо очевидного требования
(в Хаскеле применение функции записывается без скобок). Помимо очевидного требования  когда мы проверяем правильность использования именно функции
когда мы проверяем правильность использования именно функции  с точки зрения связанного с ней предиката
с точки зрения связанного с ней предиката  нужно также удостовериться в корректности выражений
нужно также удостовериться в корректности выражений  . Пусть на использование функции
. Пусть на использование функции 
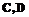 будем обозначать функцию, ставящую в соответствие Хаскел-выражению утверждение его корректности. Не будем при этом описывать конкретный критерий корректности. Полученное утверждение несомненно является правильным, однако в ряде случаев оно может оказаться сильнее, чем необходимо.
будем обозначать функцию, ставящую в соответствие Хаскел-выражению утверждение его корректности. Не будем при этом описывать конкретный критерий корректности. Полученное утверждение несомненно является правильным, однако в ряде случаев оно может оказаться сильнее, чем необходимо.
 может применяться только к положительному числу. Проверяя корректность выражения в правой части определения h в соответствии с описанным выше простым подходом, мы получим:
может применяться только к положительному числу. Проверяя корректность выражения в правой части определения h в соответствии с описанным выше простым подходом, мы получим:  .
. ) (а точнее, равняется ему) только в случае, когда первый (
) (а точнее, равняется ему) только в случае, когда первый ( ) положителен. В определении
) положителен. В определении  функции
функции  и
и  . Таким образом, проверямое выражение будет зависеть от
. Таким образом, проверямое выражение будет зависеть от  , сразу же подумают, что вычисление этого выражения начинается с вычисления аргументов. При этом аргумент
, сразу же подумают, что вычисление этого выражения начинается с вычисления аргументов. При этом аргумент  – шаблон утверждения функции f. Тогда подстановка будет иметь вид:
– шаблон утверждения функции f. Тогда подстановка будет иметь вид: .
. будет содержать переменные x и y, соответствующие параметрам функции f, а также переменные-высказывания
будет содержать переменные x и y, соответствующие параметрам функции f, а также переменные-высказывания  и Cy, которые будут соответствовать утверждениям корректности выражений, стоящих на месте параметров
и Cy, которые будут соответствовать утверждениям корректности выражений, стоящих на месте параметров  . Ее можно определять по-разному, используя возможности для ослабления утверждений. В частности, описанному выше прямолинейному подходу будет соответствовать тривиальное определение:
. Ее можно определять по-разному, используя возможности для ослабления утверждений. В частности, описанному выше прямолинейному подходу будет соответствовать тривиальное определение: 
 для ее тела, которое, конечно же, является выражением. Запишем это в виде
для ее тела, которое, конечно же, является выражением. Запишем это в виде  .
.
 .
. для подвыражений. Шаблон представляет собой конъюнкцию корректности исследуемого выражения
для подвыражений. Шаблон представляет собой конъюнкцию корректности исследуемого выражения  и корректности обеих ветвей. Главное то, что корректность каждой ветви утверждается лишь при условии, что была выбрана именно она, то есть лишь при определенном, истинном или ложном значении
и корректности обеих ветвей. Главное то, что корректность каждой ветви утверждается лишь при условии, что была выбрана именно она, то есть лишь при определенном, истинном или ложном значении 
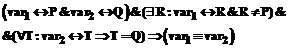 .
. – подвыражения e. Таким образом, для выражения, которое не является условным или применением функции, просто берется конъюнкция утверждений корректности его подвыражений.
– подвыражения e. Таким образом, для выражения, которое не является условным или применением функции, просто берется конъюнкция утверждений корректности его подвыражений. .
.