Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Author: () - | |
| Keywords: project solutions, analysis, , time series |
|
| Page views: 15137 |
Print version Full issue in PDF (2.59Mb) |
Сложные технические системы, такие как вычислительные сети, обладают объективной неопределенностью, что требует дальнейшего расширения инструментария прогностики. Все чаще используются интеллектуальные методы, которые расширяют классическую классификацию прогностических методов и представляют собой соче- тание формализованных процедур обработки информации, полученной по оценкам специалистов-экспертов. Исследования данных и методов анализа в последние десятилетия оформились в виде отдельного направления, называемого Times-Series Data Mining. В работах ряда зарубежных и российских ученых [1, 7–10] исследованы методы нечеткой регрессии, анализа данных нечетких временных рядов (НВР). Нечеткое преобразование (F-преобразование) – методика, разработанная И. Перфильевой [4], которая может быть отнесена к методикам нечеткого приближения. Нечеткое преобразование позволяет провести фильтрацию исходного временного ряда (ВР) и выделить тренд. Если полученный в результате F-преобразования тренд разложить на нечеткие тенденции (НТ) методом скользящего окна, то полученный итог позволяет принять управленческое или проектное решение на основе знаний о значимости тенденций. В данной статье предложен гибридный метод, сочетающий F-преобразования и НТ для принятия решений, и его применение для задач анализа эффективности эксплуатации информационных систем на основе исходных данных системных журналов. Основные определения анализа НВР. Для описания развития моделируемого процесса в лингвистических терминах введем понятие временного ряда нечетких тенденций (ВРНТ). Выделим базовые операции обработки НТ. Определение 1. НТ. Пусть Если говорить о тенденции как лингвистической переменной, терм-множеством которой является множество различных тенденций, наблюдаемых на ВР, а универсумом – множество всевозможных функций, НТ определяется как Определяя НТ на всех интервалах [t-m+1, t] ВР и позиционируя начало или окончание интервала к временной шкале, получим ВРНТ. Определение 2. ВРНТ. Пусть Для лингвистической переменной тенденция ВР определяется совокупностью значений всех видов НТ: Делая предположение о развитии системы как результата предыдущих состояний, предполагаем наличие зависимости НТ от значений тенденций в предыдущие временные промежутки. Модель НТ (МНТ). Моделью НТ с характеризующими параметрами (n,p,m,l) обозначим совокупность компонент и уравнений:
где В результате экспертного построения НТ могут возникнуть отклонения между исходным ВР и смоделированным. Обозначим данные отклонения как ошибки построения. - Ошибка построения НВР:
- Ошибка построения ВРНТ:
- Ошибка построения ВР:
Так, выбор функций принадлежности и ее параметров, метода дефаззификации определяет разницу между исходным ВР и преобразованным из НВР. Выбор видов тенденций и методов обусловливает несоответствие исходного нечеткого ряда к полученному НВР из ВРНТ. МНТ можно привести к разностному уравнению четкого ВР:
Особенности процесса распознавания НТ. Построение модели ВР – это итеративный процесс идентификации, оценки и проверки модели. Идентификация МНТ заключается в описании нечетких переменных и построении соответствующих функционалов. На этапе оценки для модели выбирается инструмент нахождения функциональной зависимости и оцениваются параметры выбранной функции по обучающей выборке. При диагностике проверяется способность модели к аппроксимации и экстраполяции. Опишем НТ в виде последовательности нечетких меток, формирующих правила распознавания, что позволит одновременно описать и дать формулу расчета степени принадлежности четкого ряда к тенденции. Совокупность всех правил определения видов НТ составляет первый уровень общей системы логического вывода МНТ, которая реализует функционал Tend для получения ВРНТ (в формализованном виде):
Множество правил уравнения МНТ составляет второй уровень вывода:
Для анализа и построения четкого ВР по нечеткой модели (функционал deTend) каждому виду НТ сопоставим НВР, имеющий наибольшую степень принадлежности. Множество таких правил, реализующее функционал преобразования ВРНТ в НВР deTend, формирует третий уровень:
Таким образом, МНТ полностью реализуется многоуровневой системой логических отношений: Использование нечеткой нейронной сети (ННС) для распознавания НТ. В качестве инструмента построения функциональной зависимости (уровень R2) в виде нечетких отношений воспользуемся аппаратом ННС. Для этого введем классические нечеткие нейроны, в которых операции сложения и умножения заменяются триангулярными нормами: И-нейрон ИЛИ-нейрон Интерпретация ННС в лингвистической форме приводит к записям: если (x1 или w1) и (x2 или w2), то b, если (b1 и z1) или (b2 и z2), то j. Веса w и z можно рассматривать как степени влияния соответствующего входа на выход. На основе таких нейронов можно построить сеть логического вывода по Мамдани для нахождения НТ, добавив в R2 весовые коэффициенты. Каждому виду НТ соответствует своя сеть. ННС состоит из двух слоев (если считать за слой нейроны): слой конъюнкции нечетких входов и слой дизъюнкции правил. Формализованно такую сеть можно выразить следующим образом:
где Преобразование. Нечеткое преобразование (F-преобразование) – методика, которая работает с непрерывной функцией Предположим, что функция Прямое F-преобразование. Определим 1) 2) 3) 4) 5) Используя базисные функции, мы преобразуем данную функцию
Обратное F-преобразование. Результатом прямого F-преобразования является вектор из чисел Можно доказать, что если F-преобразование имеет (кроме прочих) следующие свойства, важные для использования в этой статье: a) у него прекрасные фильтрующие свойства; b) его легко вычислять; c) F-преобразование стабильно относительно выбора точек
Для всех параметров установлены нечеткие переменные НВР, описывающие значения: высокое, низкое. Установлены НТ независимых параметров: загрузка, простой. Для трафика определены НТ: рост, падение, простой, скачок. Для построения модели работы узла ВС были проведены эксперименты. Анализировались модели МНТ от самого простого случая (МНТ(n,p,1,l) до моделей, включающих в себя как НВР, так и ВРНТ (МНТ(n,5,3,l ). Описание переменных
На первом этапе рассматривались модели: зависимость НВР от НВР и ВРНТ независимых переменных; зависимость НВР от НВР зависимой переменной, НВР и ВРНТ независимых переменных; зависимость НТ от НВР и ВРНТ независимых переменных. На втором этапе по наилучшим моделям составлены гибридные модели, рассмотрены линейные модели ВР с распределенным лагом (DL), с авторегрессионной составляющей (ADL) и нелинейные модели на НС, полученные в программах Statistica 6.0 и Statistica Neural Networks. Для моделирования объема трафика сервера экспертом были предложены и описаны следующие режимы работы сервера: ввод данных, чтение данных, формирование отчетов с высокими значениями тенденций параметров X1-X6. По НТ спрогнозированы низкие и высокие значения трафика, а также его четкие значения при различных режимах работы (см. рис.). Таким образом, эксперименты показывают, что модели с использованием интегрального метода F-преобразований и НТ результативны для анализа; предложенная ННС позволяет аппроксимировать сложные функциональные зависимости; построенная модель позволяет моделировать работу узла ВС и интегрировать ее в общую систему моделирования ВС. Список литературы 1. Tanaka H., Uejima S., Asai K. Linear regression analysis with fuzzy model, IEEE Trans. Systems Man Cybernet. 12, 1982, 903–907. 2. Kacprzyk J., Wilbik A. and Zadrozny S. Linguistic summarization of time series by using the Choquet integral. // IFSA’07 Theoretical Advances and Applications of Fuzzy Logic. 3. Pedrycz W., Smith M.H. Granular correlation analysis in data mining, Proc. IEEE Int. Fuzzy Systems Conf., Korea, 1999, III-1235 - IH-1240. 4. I. Perfilieva, Fuzzy transform, in: D. Dubois et al. (Eds.), Rough and Fuzzy Reasoning: Rough versus Fuzzy and Rough and Fuzzy, Springer-Verlag, Heidelberg, 2004, pp. 63–81. 5. I. Perfilieva, Fuzzy transform: application to reef growth problem, in: R. Demicco, G.J. Klir (Eds.), Fuzzy Logic in Geology, Academic Press, Amsterdam, 2003, pp. 275–300. 6. Новак В., Перфильева И., Мочкорж И. Математические принципы нечеткой логики. / Пер. с англ.: Под ред. А.Н. Аверкина. – М.: ФИЗМАТЛИТ, 2006. |
| Permanent link: http://swsys.ru/index.php?id=1596&lang=en&page=article |
Print version Full issue in PDF (2.59Mb) |
| The article was published in issue no. № 3, 2008 |
Perhaps, you might be interested in the following articles of similar topics:
- Представление процессов проектирования в функционально адаптируемой форме для хранения классов проектных решений
- Алгоритм анализа трафика в корпоративных компьютерных сетях на основе статистики экстремальных значений
- Интегральный метод принятия решений и анализа нечетких временных рядов
- Препроцессорная обработка множеств прецедентов для построения решающих функций в задачах классификации
- Кластеризация пользователей по голосу с помощью улучшенных самоорганизующихся растущих нейронных сетей
Back to the list of articles
 – НВР лингвистической переменной (
– НВР лингвистической переменной (
 ),
),  – множество НВР одинаковой длины. Тогда НТ t, определенная на
– множество НВР одинаковой длины. Тогда НТ t, определенная на  , есть совокупность упорядоченных пар
, есть совокупность упорядоченных пар  где
где  представляет собой степень принадлежности
представляет собой степень принадлежности  к НТ.
к НТ. , i=1..p, где p – количество видов НТ, определенных на ВР;
, i=1..p, где p – количество видов НТ, определенных на ВР;  – множество НВР длиной m, где
– множество НВР длиной m, где  ,
, 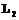 . Тогда ВРНТ есть упорядоченное во времени нечеткое множество:
. Тогда ВРНТ есть упорядоченное во времени нечеткое множество:  .
.
 ,
, 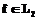


 ,
,  ,
, ,
,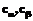 ,
, – НВР; n – количество термов НВР; Fuzzy – функционал фаззификации;
– НВР; n – количество термов НВР; Fuzzy – функционал фаззификации;  – ВРНТ; p – количество термов НТ, mj – интервал определения НТ; Tend – функционал распознавания НТ; f – функциональная зависимость; l – временной лаг;
– ВРНТ; p – количество термов НТ, mj – интервал определения НТ; Tend – функционал распознавания НТ; f – функциональная зависимость; l – временной лаг;  – НВР, полученный из ВРНТ; deTend – функционал получения НВР из оценки НТ;
– НВР, полученный из ВРНТ; deTend – функционал получения НВР из оценки НТ;  – дефаззифицированный ВР, deFuzzy – функционал получения четкого ВР из НВР.
– дефаззифицированный ВР, deFuzzy – функционал получения четкого ВР из НВР. .
. .
.
 .
. .
. .
.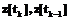 .
. , где выходы в виде нечетких переменных одного набора правил подаются на входы следующего набора правил без дефаззификации и фаззификации. Преобразования в нечеткие и четкие значения происходят только в отношениях R1 и R3 соответственно.
, где выходы в виде нечетких переменных одного набора правил подаются на входы следующего набора правил без дефаззификации и фаззификации. Преобразования в нечеткие и четкие значения происходят только в отношениях R1 и R3 соответственно. : импликация предпосылок правила;
: импликация предпосылок правила; : агрегация правил.
: агрегация правил. ,
, 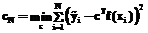 ,
, – значение, рассчитанное для некоторого вида тенденции
– значение, рассчитанное для некоторого вида тенденции  ; T – оператор конъюнкции; S – оператор дизъюнкции; r – количество правил; l, p – параметры МНТ. Основная идея обучения ННС состоит в итерационной процедуре оптимизации весов (zj,wj,i,k) и устранении незначимых связей (сокращении сети), в результате которого формируется необходимый состав и количество правил.
; T – оператор конъюнкции; S – оператор дизъюнкции; r – количество правил; l, p – параметры МНТ. Основная идея обучения ННС состоит в итерационной процедуре оптимизации весов (zj,wj,i,k) и устранении незначимых связей (сокращении сети), в результате которого формируется необходимый состав и количество правил.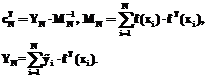 , определенной на интервале действительных чисел
, определенной на интервале действительных чисел  [4]. F-преобразование может быть использовано, помимо остальных случаев, для приближения
[4]. F-преобразование может быть использовано, помимо остальных случаев, для приближения 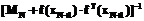 . Мы делим интервал
. Мы делим интервал  на множество равноудаленных узлов
на множество равноудаленных узлов 
 , где
, где  фиксированной длины. F-преобразование имеет две фазы.
фиксированной длины. F-преобразование имеет две фазы. базисных функций
базисных функций  , которые покрывают w, и разделим его на
, которые покрывают w, и разделим его на 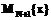 :
: ,
, , где мы формально полагаем
, где мы формально полагаем  ,
, непрерывна,
непрерывна, и монотонно убывает на
и монотонно убывает на  ,
, для всех
для всех  .
. , определенных
, определенных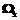 .
. .
.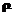 сходится к
сходится к  . Ясно, что функция
. Ясно, что функция 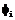 непрерывна.
непрерывна. . Это означает, что при выборе других точек
. Это означает, что при выборе других точек  (и, возможно, при изменении их числа N) результирующая функция
(и, возможно, при изменении их числа N) результирующая функция  Результаты анализа НВР на основе МНТ на примере системных журналов информационной системы. По МНТ проанализирована работа одного из узлов вычислительной сети Ульяновского государственного технического университета и создана модель узла, генерирующая нагрузку сетевого интерфейса в зависимости от параметров работы пользователей, программного обеспечения и оборудования. Узлом является сервер под ОС Microsoft Windows 2003, выполняющий приложения в терминальном режиме. Основное пользовательское приложение: базы данных «1С: Предприятие», работающее в файл-серверном режиме, где данные расположены на этом же сервере. Для описания сервера были выбраны данные из журнала событий прикладного ПО и журнала счетчиков ОС (см. табл.). Статистика собрана с 15-секундным интервалом в течение одного дня.
Результаты анализа НВР на основе МНТ на примере системных журналов информационной системы. По МНТ проанализирована работа одного из узлов вычислительной сети Ульяновского государственного технического университета и создана модель узла, генерирующая нагрузку сетевого интерфейса в зависимости от параметров работы пользователей, программного обеспечения и оборудования. Узлом является сервер под ОС Microsoft Windows 2003, выполняющий приложения в терминальном режиме. Основное пользовательское приложение: базы данных «1С: Предприятие», работающее в файл-серверном режиме, где данные расположены на этом же сервере. Для описания сервера были выбраны данные из журнала событий прикладного ПО и журнала счетчиков ОС (см. табл.). Статистика собрана с 15-секундным интервалом в течение одного дня.