Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Author: () - | |
| Keywords: quality control, algorithm, |
|
| Page views: 12339 |
Print version Full issue in PDF (8.40Mb) |
Обеспечение требуемого качества телерадиопрограмм требует сохранения на высоком уровне технических параметров оборудования, на котором осуществляются их подготовка и формирование. Для этого необходим контроль параметров оборудования, то есть в процессе эксплуатации должны осуществляться периодическая настройка и последующий контроль параметров как отдельных видов оборудования, так и технологических цепочек, в которые это оборудование входит.
Очевидно, что контроль параметров может проводиться только при наличии специального измерительного оборудования и обученного персонала, но многие телерадиокомпании не имеют средств для обеспечения комплекса ресурсных потребностей [1], включающего в себя стоимость аппаратуры, поддержание ее в рабочем состоянии, время испытаний, квалификацию персонала.
Рис. 1. Модель тракта при формировании и выдаче программ Проведем анализ вариантов алгоритма построения системы контроля качества тракта (СККТ), целью которого является максимальное снижение указанных затрат. Объектом испытаний параметров качества является тракт, объектом оптимизации – более широкая система контроля его качества. Представим модель тракта в его прямой функции, то есть в передаче программ (рис. 1). На рисунке даны следующие обозначения: Х – вектор входных переменных тракта Х[xV(t), xA(t), λ(t)], где xV(t) – вектор значений видеосигнала; xA(t) – вектор значений аудиосигнала; λ(t) – вектор в пространстве RGB длин волн света, считываемых в телекамере в данный момент (вектор λ(t) включен отдельно, так как оператор его преобразования в значение части вектора следующего далее по тракту сигнала xV(t), является отдельно измеряемым параметром цветопередачи телекамеры); Z – вектор внутренних переменных (переменных состояния) тракта [2], описываемый набором параметров, влияющих на характеристики передачи сигналов от входа к выходу и поэтому принятых для его испытаний; Y − вектор выходных переменных тракта Y[yV(t),yA(t)], определяющих степень выполнения моделью своего назначения (вектор λ(t) здесь не присутствует, так как работа не охватывает колориметрических измерений телеприемников). При переходе к построению модели СККТ следует учесть, что понятия внутренних и выходных переменных здесь меняются местами. Для выполнения трактом основной функции – формирования и передачи программ – организуется технологическая цепь с заданными в ней, согласно рисунку 1, внутренними переменными состояния Z, например, определенной формой амплитудно-частотной характеристики, чтобы обеспечить нужные параметры соответствия выходного сигнала тракта входному как конечную цель. При работе же СККТ параметры выходных сигналов тракта используются как материал для анализа, а конечной целью является вычисление параметров внутреннего состояния тракта, которые и представляют собой выходные переменные для системы контроля в целом. В результате модель функционирования СККТ как схема обработки данных имеет вид, показанный на рисунке 2.
Рис. 2. Модель СККТ
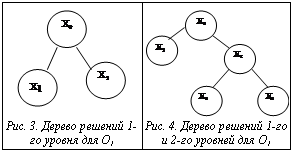
Объектом оптимизации является СККТ, целью – снижение затрат на ее организацию и функционирование. Критерий оптимальности выражает предельную меру экономического эффекта принимаемого решения для сравнительной оценки возможных альтернатив и выбора наилучшего из них. Например, это может быть максимум или минимум стоимости и т.п. [3]. Таким образом, критерием оптимальности, или целевой функции (ЦФ), в данном случае является минимум стоимости организации и функционирования СККТ. Обозначим значение ЦФ=С, тогда С= Установим принадлежность каждого из Оi совокупностям признаков Мn подсистем (ПСn) модели СККТ. Тогда 1) О1 (квалификация персонала) 2) О2 (время испытаний) 3) О3 (стоимость аппаратуры) 4) О4 (поддержание аппаратуры в рабочем состоянии) Начнем с поиска локального оптимума для каждого из Сi путем анализа состояний Оi в разных версиях развития. Используем для этого метод ветвей и границ в варианте поиска в глубину. На рисунке 3 Х0 – исходное состояние О1 (испытатель без должной квалификации); Х1 – смена О1, то есть испытателя; Х2 – смена параметров взаимодействия О1 со средой. Первый путь отвергается как бессодержательный: если бы компания могла нанять лучшего специалиста, она бы это сделала. Поэтому продолжим построение дерева от Х2 (рис. 4), где Х3 – адаптация О1 к среде взаимодействия; Х4 – адаптация среды взаимодействия к О1. Средой взаимодействия для О1, принадлежащей М1, является ПС 2. Поэтому Х3 – это профильное обучение работе по измерениям оператора, значение ЦФ которого С1 оценено в [1]: С1=(30–35) 1000 руб.×n (n – число обучаемых специалистов). При этом пренебрегаем коэффициентом неопределенности в адекватности полученных знаний, который может вести к необходимости дополнительного обучения, то есть к росту С1. Рассмотрим возможности Х4, то есть адаптации измерительной аппаратуры к оператору. Упрощение функций оператора (снижение требований к нему) достигается автоматизацией, максимальная степень которой соответствует комплексным программным решениям в аппаратуре. Таким образом, мы приходим к решению в виде программного метода генерации и анализа комплексных тест-сигналов, содержащих компоненты для измерения полного набора необходимых параметров качества. Тест-сигналы до выхода из подающей части ПС 2 в тракт и после регистрации с его выхода приемной частью ПС 2 имеют при этом форму компьютерных файлов. Такая методика, как показала практика применения разработанных для этой цели программ, пригодна к овладению ею практически любым современным специалистом с минимумом компьютерных навыков в течение дня. Соответственно, С1(Х4)<<С1(Х3). На рисунке 5 Х0 – исходное состояние О2 – время испытаний при использовании измерительного оборудования на аппаратных принципах измерений; Х1 – О2 при использовании измерительного оборудования на программных принципах измерений; Х2 – О2 при отдельных тест-сигналах для разных параметров; Х3 – О2 при комплексных тест-сигналах для полного набора параметров. Пусть С2n=k·t (Хn ), где k – коэффициент соответствия затрат С2 времени испытаний t при ситуации Хn. Он может быть нелинейным, то есть k=k(t)≠const, но, безусловно, С2=k(t)·t будет монотонно возрастающей функцией t. Поскольку очевидно, что t(Х0)>t(Х1)>t(Х2)>t(Х3), значит, С2(Х0)>С2(Х1)>С2(Х2)>С2(Х3) и решение – Х3 – совпадает с найденным для С1 в виде программного метода генерации и анализа комплексных тест-сигналов. При этом оптимизация имеет очевидный резерв Х4 – решение Х3 с дополнительным условием минимизации длительности тестовых сигналов. Поскольку произведение частоты дискретизации тест-файла на его разрядность, образующее сетевую скорость его передачи, ограничится снизу расчетом требуемой системной точности (разрешающей способности по времени и амплитуде), условие минимизации длительности адекватно условию расчетно-допустимой минимизации объема тестовых данных, которая будет рассчитываться при решении частных задач. Дерево решений 1-го и 2-го уровней для О3 имеет вид, аналогичный изображенному на рисунке 4, где Х0 – исходное состояние О3, то есть практическое отсутствие измерительной аппаратуры; Х1 – смена О3, то есть приобретение аппаратуры, предписанной ГОСТами или другой нормативной документацией; как показано в [1], этот путь экономически малодоступен и дальше не рассматривается; Х2 – смена параметров взаимодействия О3 со средой. Продолжим анализ дерева решений. Средой взаимодействия для О3, принадлежащего ПС 2, являются ПС 1 (оператор) и 3 (тракт). Для взаимодействия ПС 1 с ПС 2 оптимум уже найден, и можно не возвращаться к этому при условии, что дальнейшая оптимизация не войдет с ним в противоречие. Таким образом, следующий уровень дерева относится к взаимодействию О3 с ПС 3 – испытуемым трактом. Х3 – адаптация среды взаимодействия (ПС 3) к О3. Путь невозможен – тракт (ПС 3) таков, какой он есть. Х4 – адаптация О3 к среде взаимодействия, то есть организация работоспособного комплекса измерительной аппаратуры. Отвергнутый путь Х1 означал комплект аппаратуры по перечням НД, следовательно, ищется альтернатива, сочетающая минимум цены с широкими измерительными возможностями. Сегодня она однозначно ясна – использование в качестве средств измерений компьютеров с платами ввода-вывода аудиовидеосигналов и целевым программным обеспечением, что и является решением Х4. При наличии соответствующей программы стоимость оборудования, то есть одного или двух компьютеров для измерений того же набора аудио- и видеопараметров, снижается более чем на порядок: С3(Х4)<<С3(Х1). Однако цепь оптимизации параметра С3 еще не закончена (рис. 6).
Средства измерений параметров трактов должны обладать следующими свойствами: 1) способностью выдачи в тракт и приема из него видео- и аудиосигналов; 2) способностью к анализу поступившей информации по алгоритмам методик измерений; 3) гарантированной точностью измерений и возможностью периодического подтверждения этой точности. Первой способностью CНМ и ЗС обладают по определению. Способность к должному анализу поступившей информации обеспечивается разработанной для этого программой. Вопрос же о точности и поверке измерительной установки в его аппаратном аспекте не рассматривается, так как параметры станции и являются, собственно, органической составляющей параметров тракта и его продукции в целом. Таким образом, компьютерные средства выдачи и приема аудиовидеосигналов, входящие в состав комплексов формирования теле- и радиопрограмм, могут использоваться для измерений параметров трактов с помощью специально разработанных программных средств.
Рис. 7. Модель СККТ в варианте Х5 Поскольку С3(Х5)=0, данное решение можно считать глобальным оптимумом. Модель СККТ в этом случае примет вид, показанный на рисунке 7. На рисунке 7 место ПС 2 занимает испытуемый тракт 2, осуществляющий, по определению ГОСТ 19.701-90, предопределенный процесс, состоящий из одной или нескольких операций или шагов программы, которые определены в другом месте (в подпрограмме, в модуле). Определение процесса производится оператором 1, инсталлирующим в выбранную компьютерную станцию (станции) конкретную измерительную программу и организующим прохождение сигналов в тракте по нужной траектории. Оператор 1 получает на выходе ПС 2 не поток данных В (в разных комплексах в разной степени обработанных; в принципе это могут быть и осциллограммы или даже показания стрелочных приборов), а измеренные значения Y′ полного набора видео- и/или аудиопараметров Y тракта для передачи в пункт принятия решений 3. Широкое использование данной возможности требует в качестве дополнительного условия выбора формата тестовых файлов универсального применения. А именно, тестовый файл, передаваемый на объект испытаний, должен либо воспроизводиться на выходе станции в той или иной форме видео- или аудиосигнала, либо быть преобразованным в рабочий формат станции, который позволяет осуществить такое воспроизведение. Решение Х5 является глобальным оптимумом также и для С4, так как дополнительных к тракту объектов поддержания работоспособности не возникает. Поскольку ни один из найденных оптимумов для Сi не включает элементов противоречия другим, можно заключить, что их совокупность является и минимумом ЦФ С= В итоге системная оптимизация алгоритма контроля качества телерадиопродукции должна отвечать следующим общим требованиям: 1) программный метод генерации и анализа тестовых файлов; 2) расчетно-допустимая минимизация объема тестовых данных; 3) использование тестовых форматов универсального применения. Алгоритм, отвечающий данным требованиям, можно назвать методом универсальных тестовых файлов. Метод допускает этапность в реализации его принципов, а также применение дистанционной диагностики. Список литературы 1. Мкртумов А.С. Дистанционная диагностика трактов радиовещания. // Матер. Междунар. конгр. НАТ: Москва, TRBE’2006. – М., 2007. 2. Гладков Л.А., Курейчик В.М., Курейчик В.В. Генетические алгоритмы. – Р.-н.-Д.: ООО «Ростиздат», 2004. – 400 с.3. Коляда А.В. и др. Разработка методов и алгоритмов принятия решений при проектировании на основе квантовых вычислений. – Таганрог: Изд-во ТТИ ЮФУ, 2007. – 155 с. |
| Permanent link: http://swsys.ru/index.php?id=1645&lang=en&page=article |
Print version Full issue in PDF (8.40Mb) |
| The article was published in issue no. № 4, 2008 |
Perhaps, you might be interested in the following articles of similar topics:
- Рекурсивный алгоритм точного расчета ранговых критериев проверки статистических гипотез
- Эффективная программная реализация вейвлет-преобразования
- Способы реализации алгоритмов интегральных преобразований изображений по линиям
- Система непрерывного мониторинга и управления качеством производства стеклодротов
- Комплекс программ идентификации точечных дефектов листового стекла
Back to the list of articles


 На рисунке даны обозначения символов операторов по ГОСТу 19.701-90 (ИСО 5807-85): 1 – подсистема (ПС) действий оператора (человека) по организации процесса испытаний, включая подачу тестовых сигналов и анализ выходных данных; 2 – ПС подачи тестовых сигналов на вход тракта и регистрации и анализа выходных сигналов тракта; 3 – ПС «испытуемый тракт»; 4 – ПС синтеза результирующей оценки с переключением на коррекцию тракта (ПС 3); 5 – ПС действий по коррекции ПС 3 при несоответствии требованиям; 6 – пункт назначения данных/конец работы алгоритма; А – поток данных (ручных команд) от 1 к 2; Х – вектор входных переменных тракта; Y – вектор выходных переменных СККТ (он же – вектор внутренних переменных тракта 3); Z – вектор внутренних переменных СККТ (он же – вектор выходных переменных тракта 3); В – поток выходных данных подсистемы 2 к испытателю 1; Y′ – измеренные значения полного набора видео- и/или аудиопараметров Y тракта.
На рисунке даны обозначения символов операторов по ГОСТу 19.701-90 (ИСО 5807-85): 1 – подсистема (ПС) действий оператора (человека) по организации процесса испытаний, включая подачу тестовых сигналов и анализ выходных данных; 2 – ПС подачи тестовых сигналов на вход тракта и регистрации и анализа выходных сигналов тракта; 3 – ПС «испытуемый тракт»; 4 – ПС синтеза результирующей оценки с переключением на коррекцию тракта (ПС 3); 5 – ПС действий по коррекции ПС 3 при несоответствии требованиям; 6 – пункт назначения данных/конец работы алгоритма; А – поток данных (ручных команд) от 1 к 2; Х – вектор входных переменных тракта; Y – вектор выходных переменных СККТ (он же – вектор внутренних переменных тракта 3); Z – вектор внутренних переменных СККТ (он же – вектор выходных переменных тракта 3); В – поток выходных данных подсистемы 2 к испытателю 1; Y′ – измеренные значения полного набора видео- и/или аудиопараметров Y тракта.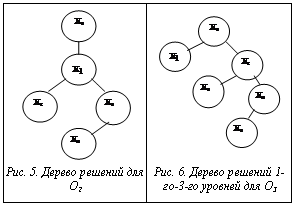 Х5 отличается от Х4 тем, что функцию средств измерений выполняют компьютерные системы из состава тракта формирования программ 3. В настоящее время практически в каждой телерадиокомпании в тракт формирования и выдачи программ вошли компьютерные средства выдачи и приема аудиовидеосигналов (станции нелинейного видеомонтажа (СНМ), звуковые станции (ЗС), серверы), работающие с их файловым представлением. Рассмотрим возможности их использования для контроля состояния трактов.
Х5 отличается от Х4 тем, что функцию средств измерений выполняют компьютерные системы из состава тракта формирования программ 3. В настоящее время практически в каждой телерадиокомпании в тракт формирования и выдачи программ вошли компьютерные средства выдачи и приема аудиовидеосигналов (станции нелинейного видеомонтажа (СНМ), звуковые станции (ЗС), серверы), работающие с их файловым представлением. Рассмотрим возможности их использования для контроля состояния трактов.
