Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: Arefiev I.B. (i.arefyev@am.szczecin.pl) - Marine Academy, Shchetsin, Ph.D, () - | |
| Keywords: , , , , |
|
| Page views: 7921 |
Print version Full issue in PDF (3.60Mb) |
Современные технологии моделирования сложных процессов и систем все более ориентируются на интеграцию отдельных собственных элементов по их математическому описанию и соответствию отдельных процедур для решения основной задачи – минимизации стоимости и времени на разрешение ситуаций. В этом отношении транспортные системы не являются исключением. Настоящая работа посвящена одному из решений данной задачи, которое основано на создании модели системы управления транспортным узлом (ТУ) на базе распределения Гаусса. При создании процедур принятия и поддержки решения по управлению в современных системах управления транспортом часто используют политранспортные модели, когда конкретные процедуры перевозки единицы груза не формируются, а создаются мультимодальные системы из разных видов единиц-перевозчиков для минимизации процесса доставки единицы груза по критериям минимума стоимости и времени. В работах [1,2] показано, что в определенных условиях управление грузопотоком в ТУ подчиняется распределению Гаусса. Тогда для объектов подобного типа справедливо следующее утверждение. Допустим, что X1,…,Xn является переменной из Q нормального распределения с неизвестной средней точности R. Тогда условное разложение переменной Q при R=r (r>0) является нормальным распределением со средней Отсюда совместное апостериорное распределение переменных Q и R при условии, что Xi=xi (i=1,...,n), будет трактоваться как условное разложение случайной переменной Q и R=r и окажется нормальным разложением со средней m¢ и точностью (t+n)r, при этом:
a граничное распределение переменной R является гамма-распределением с параметрами
В некоторых задачах информация, полученная для Q до начала наблюдения о состоянии ТУ, может быть значительно меньше по сравнению с информацией, которая ожидается при завершении анализа совокупного состояния ТУ. В задачах такого типа выбор и обоснование распределения заранее не могут быть весьма простыми, даже если найти соответствующее семейство распределений параметра Q. В таких случаях принимается стандартное распределение генерального параметра, понимая, что используется неточное распределение. Если принять, что плотность такого разложения является плотностью равномерного распределения на всей вещественной прямой, то она не является плотностью истинного разложения. В ряде случаев можно получить распределение, близкое к реальному. Для этого рассмотрим задачу, сформулированную в утверждении. Пусть случайная выборка X1,…,Xn берется из распределения, для которого неизвестны параметры Q и R согласно утверждению о совместном распределении параметров Q и R, тогда h( Условное распределение переменной Q при R=r оказывается нормальным распределением, при том что конечное распределение переменной Q не является нормальным распределением. Частоту конечного распределения переменной Q найдем как
Если использовать символы пропорциональности и принять все факторы, исключающие q, то на основании (3) функция g примет вид:
Сопоставление данной функции с частотой изменения состояния ТУ по позиции времени t со ступенями a показателя отклонения m и точностью вычисления t получим g(y| = Приведем пример, иллюстрирующий полученный результат. Рассмотрим нормальное распределение, в котором средние значения q и R неизвестны. Необходимо найти гамма-распределение из группы распределений, представляющих априори переменные q и R. Как будут выбраны показатели m,t,a и b, если E(q)=2, Решение. Поскольку R принято как гамма-распределение с параметрами a и b, справедливо E(R)=3=
Отсюда t=0,1. Таким образом, получено решение для распределения переменных q и R. Для окончательного подтверждения полученного теоретического результата приведем еще один пример реализации. Пусть нормальное распределение выведено из 10 наблюдений, при этом получено Необходимо найти среднее значение и варианты распределения заранее известных переменных q и R при условии Решение. Согласно (6), параметры m¢, t¢, a¢ и b¢ заранее распределены для переменных q и R и определены как m¢=4,18, t¢=10,1, a¢=8 и b¢=3,94. На основании этих значений получим среднее для вариантов состояния переменных q и R: E(q)=4,18; D2(q)=0,056; E(R)=2,03 и D2(R)=0,515. Отсюда также находим m¢¢=4,33, t¢¢=20,1, a¢¢=13 и b¢¢=7,08, E(q)=4,33, D2(q)=0,029, E(R)=1,84 и D2(q)=0,029, E(R)=1,84, D2(R)=0,260. Получаем изменение q в распределении t с 26 степенями свободы при m¢¢=4,33 с точностью a¢¢t¢¢/b¢¢=36,9. Следовательно, Теперь можно утверждать, что интервал доверия q на уровне состояния 0,05 приводится к виду Предложенная методика была использована для создания модели принятия решения по управлению политранспортным терминалом в фирме «Stowarzyszenie armotorów rybackich. ZACLAD GLÓWNY» (Польша). Литература 1. Пасевич В. Анализ и прогнозирование транспортных систем. – СПб: Система, 2006. – 83 с. 2. Арефьев И.Б., Пасевич В. Управляемая модель транспортного узла на базе распределения Гаусса. // Тр. Междунар. конф.: Математика в инженерных и экономических расчетах. – СПб: ГУВК, 2001. – С. 37–40. |
| Permanent link: http://swsys.ru/index.php?id=2015&lang=en&page=article |
Print version Full issue in PDF (3.60Mb) |
| The article was published in issue no. № 1, 2009 [ pp. 41 ] |
Back to the list of articles
 и точностью t (r>0), а граничное распределение R является гамма-распределением с параметрами a>0 и b>0.
и точностью t (r>0), а граничное распределение R является гамма-распределением с параметрами a>0 и b>0. , (1)
, (1)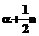 и b¢, где
и b¢, где . (2)
. (2) ,r)
,r) . (3)
. (3)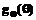 =
= , для q
, для q . (4)
. (4)

 . (5)
. (5)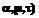 =
= . (6)
. (6) =5, E(R)=3,
=5, E(R)=3,  =3?
=3?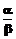 и
и  , получаем a=3 и b=1, при m=2, когда E(q)=m. Принимая распределение q по дискрету t со степенями свободы как 2a при точности
, получаем a=3 и b=1, при m=2, когда E(q)=m. Принимая распределение q по дискрету t со степенями свободы как 2a при точности  , получим:
, получим: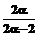
 =
= . (7)
. (7) =4,20 и
=4,20 и  =5,40.
=5,40. =4,48 и
=4,48 и  = =5,82. Апостериорным распределением наблюдения определим новое распределение R и доверительный интервал q на уровне величины 0,05.
= =5,82. Апостериорным распределением наблюдения определим новое распределение R и доверительный интервал q на уровне величины 0,05.
 =0,95.
=0,95. .
.