Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Author: () - | |
| Keywords: , , , intelligent transport systems |
|
| Page views: 10456 |
Print version Full issue in PDF (3.60Mb) |
В основе организации и в управлении транспортными системами заложены принципы се- тевых процессов, которые интегрируют в себе основные целевые функции реализации доставки грузов по схеме «производитель–потребитель». Это позволяет достигать поставленных целей, выбирая рациональные решения в так называемых интеллектуальных транспортных системах. В данной работе автор предлагает метод идентификации ошибочных решений в транспортной системе. Совершенствование работы транспортных систем рассматривается в [1–4]. Особенно это касается так называемых интеллектуальных транспортных систем. Интеллектуальная транспортная система [3] – это комплекс современных информационных и телекоммуникационных технических средств, объединенных с процессами принятия решений, задачей которых является оптимизация работы транспортной системы в целом. Базовым элементом интеллектуальных транспортных систем является соответствующая технологическая и информационная инфраструктура. К основным проблемам относятся организация, управление и координация грузопотоков в транспортных системах и узлах (ТУ). Информация, локализованная в диспетчерской системе ТУ, и принятые методы расчета могут служить основой для принятия рациональных решений в организации технологических процессов. В работе [2] представлен метод идентификации (классификации) согласно квадратичной дискриминационной функции. Неизвестные параметры данной функции заменены соответствующими параметрами, где проведено исследование традиционных характеристик подобной зависимости. В работе [4] были найдены вероятности ошибочной линейной классификации дискриминационной функции и вероятности ошибочной классификации квадратичной дискриминационной функции в случае одномерного нормального распределения, в котором была принята известность данных параметров. Следует добавить, что в общем случае дискриминационной функции при неизвестности параметров вероятности ошибочной классификации не были обнаружены. Допустим, что в классификации параметров при использовании линейной дискриминационной функции данные известны частично, найдем для такой ситуации вероятность ошибочной классификации. Примем, что в ТУ дано наблюдение х случайного вектора X, происходящее с одной из двух p-размерных нормальных популяций В случае известности параметров mi и Si квадратичная дискриминационная функция определяется формулой
Используя известную теорию принятия решений [1,5], получим, что наблюдение х происходит из популяции p1, если
и Далее считаем, что q1=q2=1/2, где Тогда k=0. Если S1=S2=S, то функция (1) редуцируется до вида
Функция (3) известна как линейная дискриминационная функция [1]. Найдем вероятности ошибочной линейной классификации дискриминационной функции, принимая, что ее параметры частично известны, то есть векторы средних различны, m1¹m2, но известны, а матрицы ковариации равны, то есть S1=S2=S. Пусть F означает дистрибутанту стандартизированного нормального разложения, и тогда
Выражение (4) будет оценкой общей матрицы ковариации S, где решение означает обучающую попытку из популяции pi (i=1,2; j=1,…,ni, n1+n2=n³p). Оценка S является параметром наибольшей достоверности неизвестного параметра S. Подставляя вместо параметра S его оценку s в равенство (3), получаем дискриминационную статистику для реализации вектора х в виде
Отметим, что разложение случайной функции E =E = и вариацией
=E{[ [ = = Таким образом, вероятность
=F =F Таким же образом можно показать, что вероятность
Производя идентификацию наблюдения х относительно популяции p1 или p2 и опираясь на линейную дискриминационную функцию (3), закладываем известность параметров m1,m2 и S. Однако в случае, когда параметры эти известны частично, то есть когда неизвестен параметр S, примем его за S. Если
Функция (8) не должна быть оптимальной в смысле подхода теории принятия решения в ее классификации. Теперь докажем, что правило идентификации согласно функции (8) – это правило наибольшей вероятности. Считается, что правило идентификации является правилом наибольшей вероятности, если наблюдение х классифицируем в популяцию p1 в случае Действительно, заметим, что
также
= = где tr обозначает след квадратичной матрицы, то есть сумму элементов на ее главной диагонали. Отсюда
Аналогично L1 Предложенное решение полностью соответствует поведению ТУ, когда идентификация груза должна соответствовать типу и виду транспортных средств. Решение настоящей задачи может быть положено в основу АСУ диспетчированием ТУ на оперативном уровне. Литература 1. Anderson T.W. An Introduction to Multivariate Statistical Analysis, J.Wiley, New York, 1966. 2. Ariefiew I.B., Pasewicz W. Analysis of Quality Discriminant Function in Identyfication of Transport Junction, Trudy rosyjsko-polskiej konferencji: Analiz, Prognozirowanije i Uprawlenije w Słożnych Sistiemach, (APS-2002), Sankt Petersburg, 2002. 3. Chwesiuk K. Inteligentne Systemy Transportowe- ich Istota i Światowy Rozwój, Trudy rosyjsko-polskiej konferencji: Analiz, Prognozirowanije i Uprawlenije Słożnych Sistiemach, (APS-2003), Sankt Petersburg, 2003. 4. Pasewicz W. Nieprawilnaja Klasifikacja Wierojatnostiej dlia Klasificirujuszcziej Funkcji w Transportnom Uzlie, Trudy rosyjsko-polskiej konferencji: Analiz, Prognozirowanije i Uprawlenije w Słożnych Sistiemach, (APS-2002), Sankt Petersburg, 2002. 5. Wald A. Statistical Decision Functions, J. Wiley, New York, 1950. |
| Permanent link: http://swsys.ru/index.php?id=2017&lang=en&page=article |
Print version Full issue in PDF (3.60Mb) |
| The article was published in issue no. № 1, 2009 [ pp. 45 ] |
Perhaps, you might be interested in the following articles of similar topics:
 , i=1,2, с известными вероятностями априори qi (q1+q2=1), где mi – p-размерный вектор средних, а Si дополнительно является определенной матрицей ковариации с размерами (p´p).
, i=1,2, с известными вероятностями априори qi (q1+q2=1), где mi – p-размерный вектор средних, а Si дополнительно является определенной матрицей ковариации с размерами (p´p). (1)
(1)
 , так же х выводится из популяции p2, если
, так же х выводится из популяции p2, если  , (2)
, (2) является потерей в результате ошибочной классификации x относительно p1(p2).
является потерей в результате ошибочной классификации x относительно p1(p2). .
.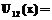
 (3)
(3) . (4)
. (4)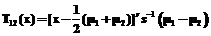 . (5)
. (5) при условии X~N(m1,S) является нормальным разложением со средней
при условии X~N(m1,S) является нормальным разложением со средней
 =
= =
=
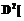

 |X
|X
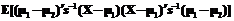 =
=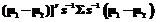 .
.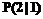 может быть ошибочной классификацией, то есть классифицирование наблюдения х относительно популяции p2 есть время наблюдения фактически происходящего процесса из популяции p1:
может быть ошибочной классификацией, то есть классифицирование наблюдения х относительно популяции p2 есть время наблюдения фактически происходящего процесса из популяции p1: ]=
]= =
= . (6)
. (6) происходит из популяции p2 и равна
происходит из популяции p2 и равна . (7)
. (7)
 , то наблюдение х происходит из популяции p1, а если
, то наблюдение х происходит из популяции p1, а если  . (8)
. (8)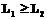 , а также х классифицируем в популяцию p2 при
, а также х классифицируем в популяцию p2 при  , где
, где  (i=1,2) является функцией вероятности нормального разложения [1].
(i=1,2) является функцией вероятности нормального разложения [1]. =
= ; i=1,2, (9)
; i=1,2, (9) ´
´

 exp{
exp{ =
= ; i=1,2,
; i=1,2,

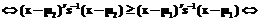

 .
. означает, что правило идентификации с основой на функцию (8) является правилом наибольшей вероятности.
означает, что правило идентификации с основой на функцию (8) является правилом наибольшей вероятности.