Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Author: () - | |
| Keywords: , , optimization methods, |
|
| Page views: 13607 |
Print version Full issue in PDF (3.60Mb) |
Повышение значимости банковской системы в российской экономике позволяет определить как одну из приоритетных задачу повышения устойчивости и эффективности функционирования кредитных организаций. Данное положение было закреплено в Стратегии развития банковского сектора Российской Федерации на период до 2008 г. в качестве основной цели на среднесрочную перспективу. Одним из основных условий обеспечения устойчивого развития кредитной организации является эффективное управление активами и пассивами предприятия, которое возможно с помощью методов и моделей портфельной оптимизации. Данный инструментарий позволяет решить задачу формирования эффективного портфеля кредитной организации посредством определения таких пропорций распределения средств между допустимыми активами, которые обеспечат минимальный риск портфеля при определенном (заданном) уровне доходности. Исторически первым математическую модель формирования оптимального портфеля в статическом случае как задачу исследования операций и теории игр сформулировал Г. Марковиц [1]. Публикации ученого вызвали большой поток научных работ по финансовой теории и теории исследования операций (например [2,3]). Интерес к использованию методов оптимизации при формировании эффективного портфеля огромен, при этом наиболее перспективными представляются исследования, связанные с динамическими моделями управления активами и пассивами. Целью данной публикации является аналитический обзор проблем и перспектив практического использования моделей данного вида в деятельности предприятий банковского сектора. Динамические модели управления активами и пассивами относятся к классу оптимизационных моделей, позволяющих учесть возможность будущей перестройки портфеля финансовых инструментов, которая непосредственно связана с транзакционными издержками: совокупная величина таких издержек зависит от частоты возможных перестроек. Такой способ построения исследуемых моделей получил название «Asset and Liability Management» (ALM) – управление активами и пассивами (см., например, [4]). Среди основных подходов, используемых для реализации данных моделей, принято выделять решающие правила выбора стратегий, наращивание капитала, стохастическое управление, стохастическое программирование. Наиболее эффективным, по мнению автора, является использование в процессе управления банковскими активами и пассивами методов многоэтапного стохастического программирования, ключевая идея которого состоит в генерировании множества сценариев реализации случайных параметров в виде дерева и выборе управлений в вершинах дерева [5]. Использование данного подхода на практике позволяет учесть множество особенностей реального мира, а именно – ограничения на оборотные средства, операционные издержки, неприятие риска, налоги, предельные ограничения на группы активов и иные соображения. Концепция ALM предполагает, что состояние портфеля кредитной организации рассматривается в фиксированные моменты времени, в каждый из которых инвестор принимает решения, касающиеся структуры портфеля, а также его финансовых целей. Кроме того, требуется учитывать факторы неопределенности, которые могут принимать случайные значения в каждый из рассматриваемых моментов и представлять собой различные характеристики банковского портфеля, а также зависимости между рассматриваемыми факторами. В модели ALM генерируются сценарии изменения случайных факторов, имеющие древовидную структуру, данный процесс происходит на основе использования исторических данных, особенности которых также должны учитываться. Обязательным является использование в динамической модели оптимизации банковского портфеля двух основных уравнений для финансовых потоков, посредством которых набор ключевых экономических факторов соотносится с остальными переменными модели, такими как показатели доходности активов и пассивов [4]. 1. Для активов j-й категории в случае реализации s-сценария:
где 2. Для потока платежей и поступлений в случае реализации s-сценария:
где Принципиально для многошаговой модели ограничение вида В каждый момент состояние в модели оценивается некоторой целевой функцией, а управление осуществляется путем перераспределения между категориями активов, корректировки выплат задолженности и осуществления заданных целевых выплат. Кроме того, налагаются ограничения на динамический процесс: предельные доли заемных средств, операционные издержки, иные ограничения. Цель исследования посредством построения рассматриваемой динамической модели состоит в отыскании допустимой точки в заданные периоды времени, где максимального значения достигает целевая функция, связывающая оптимизируемые переменные с управляемыми, то есть позволяющая оценить финансовые риски, а также потенциал денежных вознаграждений за их принятие. Поскольку рассматриваются неопределенности во времени, оптимальное решение будет выбираться из множества путей изменения доходности банковского портфеля. Одной из основных проблем использования на практике динамических моделей управления банковскими активами и пассивами, выделяемых в отечественных научных разработках [5], явля- ется необходимость учета особенностей деятельности, принципов работы и опыта прошлого развития конкретного предприятия банковского сектора. Построение динамической модели в конкретном случае требует учета единственного в своем роде многочисленного набора исходных данных, на базе которого должен быть построен уникальный, логически непротиворечивый и основанный на здравых экономических принципах сценарий развития событий. Параметры генератора сценариев должны подгоняться к архивной базе данных и к опыту прошлого развития, а стохастическая модель должна учитывать не только изменчивость экономических условий, но и особенности поведения конкретного субъекта управления, его расположенность к риску. Преодолению данной проблемы может во многом способствовать разработка собственной уникальной компьютерной системы для оценки решений по размещению активов, качество функционирования которой во многом определится квалификацией сотрудника банка, ответственного за проектировку данной системы. Другие проблемы, связанные с практическим применением рассматриваемых оптимизационных моделей, касаются вычислительных трудностей, которые возникают из-за свойств дерева сценариев, лежащего в основе стохастического программирования. Число переменных, участвующих в решении, нарастает экспоненциально [5]. При этом в большинстве случаев можно обрезать дерево, намеренно сокращая число ветвей, исходящих из вершин, особенно для вершин, расположенных ближе к горизонту планирования. Не менее актуальными являются также проблемы, связанные с необходимостью использования высокоэффективных алгоритмов при реализации динамического управления банковским портфелем методами многоэтапного стохастического программирования из-за огромного числа переменных, участвующих в решении. Основные алгоритмы для получения решений в стохастическом программировании, использующие специфику древовидной структуры множества сценариев, можно разделить на три группы: прямые методы, прежде всего методы внутренней точки, методы декомпозиции Бандерса и методы декомпозиции на основе модифицированных функций Лагранжа. В настоящее время возможно решать задачи нелинейного стохастического программирования с числом сценариев свыше 10 000, и, что более важно, время счета по программе является линейной функцией числа сценариев. Таким образом, учитывая рост быстродействия компьютеров на 40–50 % в год, аналогично можно наращивать размерность задач стохастического программирования. В то же время не следует забывать о необходимости компромисса между реалистичностью модели и удобством ее использования. Среди возможных направлений будущих исследований в области развития динамических моделей можно выделить, во-первых, реализацию логически обоснованной потребности в робастных оценках, например, доверительных интервалов, а также предлагаемых рекомендаций определенной модели данного класса. Такая оценка менее чувствительна к малым отклонениям от предположений, различным неоднородностям в выборке, связанным с теми или иными, в общем случае неизвестными, причи- нами. Во-вторых, для успеха долгосрочного планирования решающее значение будет иметь общепринятое определение риска с учетом факторов времени, которое во многом может способствовать определению приоритетов при ведении активной инвестиционной деятельности предприятиями банковского сектора. Теория многоцелевой оптимизации владеет рядом многообещающих технических приемов для оказания помощи инвесторам при анализе их будущих возможностей. В заключение отметим, что динамические модели ALM как наиболее эффективный метод решения задачи формирования банковского портфеля нашли свое наиболее успешное применение в сфере долгосрочного финансового планирования деятельности коммерческих банков, где необходимость неоднократного принятия решений определяется сущностью процесса. В рамках данных моделей возможен учет таких основных моментов в практическом финансовом планировании, как ограничения институционального характера, финансовые потоки с их неопределенностями, операционные издержки, налогообложение и пр. Аналитический обзор существующих проблем практического использования динамических моделей управления активами и пассивами позволяет наметить основные способы их решения и определить перспективы применения таких моделей конкретной организацией. Литература 1. Markowitz H.М. Portfolio Selection. // Journal of Finance. 1952, vol. 7, № 1. 2. Первозванский А.А., Первозванская Т.Ю. Финансовый рынок: расчет и риск. – М.: Инфра-М, 1994. 3. Касимов Ю.Ф. Основы теории оптимального портфеля ценных бумаг. – М.: Филинъ, 1998. 4. Mulvey J.M., Ziemba W.T. (eds.) Asset and liability management systems for long-term investors: discussion of the issues. Worldwide asset and liability modeling. – Cambridge University Press, 1998. 5. Ерешко А.Ф. Методы декомпозиции и локально-оптимальные стратегии в задачах управления портфелем ценных бумаг. – М.: Науч. изд. ВЦ им. А.А. Дородницына РАН, 2002. |
| Permanent link: http://swsys.ru/index.php?id=2031&lang=en&page=article |
Print version Full issue in PDF (3.60Mb) |
| The article was published in issue no. № 1, 2009 [ pp. 77 ] |
Perhaps, you might be interested in the following articles of similar topics:
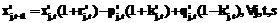 ,
, и
и  – суммарная стоимость финансовых инструментов (активов) j-го типа в моменты t и t+1 соответственно;
– суммарная стоимость финансовых инструментов (активов) j-го типа в моменты t и t+1 соответственно;  – процентная ставка за период от t до t+1 по инструменту j;
– процентная ставка за период от t до t+1 по инструменту j;  – продажа инструмента j;
– продажа инструмента j;  – покупка инструмента j;
– покупка инструмента j; 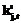 – транзакционные издержки операций с финансовыми инструментами.
– транзакционные издержки операций с финансовыми инструментами.
 – разность поступления и оттока средств в момент t;
– разность поступления и оттока средств в момент t;  и
и  – количество наличных средств в моменты t+1 и t соответственно;
– количество наличных средств в моменты t+1 и t соответственно;  – платежи по j-му инструменту в момент t (сюда относятся, например, купонные платежи по облигациям, дивиденды по акциям, выплата процентов и погашение кредитов).
– платежи по j-му инструменту в момент t (сюда относятся, например, купонные платежи по облигациям, дивиденды по акциям, выплата процентов и погашение кредитов). [4,5] для всех сценариев s1 и s2, унаследовавших общее прошлое вплоть до момента t. Иначе говоря, все сравниваемые варианты должны иметь одинаковые предыдущие решения.
[4,5] для всех сценариев s1 и s2, унаследовавших общее прошлое вплоть до момента t. Иначе говоря, все сравниваемые варианты должны иметь одинаковые предыдущие решения.