Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: () - , () - | |
| Keywords: numerical computation, , , dynamic systems |
|
| Page views: 8606 |
Print version Full issue in PDF (4.72Mb) |
Проблема построения управления с обратной связью в нелинейных управляемых системах до сих пор остается актуальной и находится в центре внимания специалистов по управлению. Для решения задач оптимального позиционного управления (ЗОПзУ) нелинейными дифференциальными системами известны различные методики. Специфической чертой подхода Н.Н. Моисеева [1] является возможность декомпозиции ЗОПзУ с аддитивным целевым функционалом на элементарные задачи за счет реализации принципа оптимальности Р. Беллмана на априорных «шкалах состояний» в пространстве «время–состояния». Известный метод «блуждающих трубок» [1], призванный дать оценку области, в которой требуется введение шкал состояний, при данных начальном и/или целевом множествах обеспечивает локальное решение задачи, будучи определенным на некоторых подмножествах трубок достижимости и/или разрешимости (управляемости). Эффективность подхода определяется суммарной трудоемкостью значительного числа элементарных операций по вычислению траектории системы для перехода из каждого узла на дискретном множестве состояний, введенном для одного узлового момента времени, в каждый узел на аналогичном множестве для последующего узла по времени. Иными словами, требуется найти (по возможности глобальное) решение задачи оптимального программного управления (ЗОПрУ) для рассматриваемой динамической системы при терминальных ограничениях. Конструктивными направлениями в развитии подхода Н.Н. Моисеева представляются: 1) предварительная аппроксимация трубки достижимости при заданном начальном множестве или трубки разрешимости при данном целевом множестве; 2) решение ЗОПрУ на основе современных алгоритмических и программных средств. Конструктивное развитие схемы Моисеева предложено в работах [2–4] с приложениями к различным модельным задачам. Формулировка задач оптимального управления Рассматривается управляемая система
где управление программное u=u(t) или позиционное u=u(t, x). Классы доступных программных и позиционных управлений:
Множеством достижимости R(tI, xI, tI) системы (1) из позиции {tI, xI} (tS≤tI Трубкой достижимости, обозначаемой R(tI, xI, (tI, tII]), системы (1) из позиции {tI, xI} на полуотрезке (tI, tII] (tS≤tI. Аналогично определяются множества и трубки достижимости из компакта X(tI), лежащего на гиперплоскости, пересекающей пространство позиций при Целевым множеством M назовем компакт, лежащий на гиперплоскости, пересекающей пространство позиций в момент tF, на который требуется привести систему (1) при всевозможных доступных управлениях. Множеством разрешимости (M-управляемости), обозначаемым Трубкой разрешимости, или трубкой M-управляемости, обозначаемой Поточечные фазовые ограничения
Относительно системы (1) с заданным целевым множеством M, множеством начальных состояний X(ts), имеющим непустое пересечение с W(tS, tF, M), рассматривается ЗОПзУ с целевым критерием Решением ЗОПзУ будем называть функцию Схема численной оптимизации позиционных управлений Для реализации подхода необходимо ввести в рассмотрение понятия аппроксимации целевого множества, трубки разрешимости и аппроксимирующего позиционного управления. Сечение трубки разрешимости – множество разрешимости, является также множеством достижимости системы, получаемой из исходной при ее рассмотрении в обратном времени с целевым множеством как множеством начальных состояний. Множества достижимости нелинейных систем могут быть невыпуклыми и несвязными, и поэтому для учета этих особенностей в работе [2] предложены алгоритмы, реализующие метод сечений для аппроксимации множеств, а для ряда тестовых примеров представлены результаты численных экспериментов, иллюстрирующих эффективность метода сечений. На отрезке [0, tF], рассматриваемом в прямом времени, вводится сетка с шагом Вводится также сетка, узлы tr Аппроксимацией (ограниченного) множества разрешимости W[tj] системы (1), рассматриваемого в момент
Аппроксимацией (ограниченной) трубки разрешимости В основу метода сечений [2] положена следующая идея построения контура множества достижимости системы в момент tj: 1) находятся координаты параллелепипеда, всех граней которого изнутри касается множество достижимости – для этого решается серия ЗОПрУ с целью поиска экстремальных (по возможности в глобальном смысле) значений каждой фазовой переменной; 2) в границах параллелепипеда вводится сетка с разбиением по каждой координате; 3) в результате решения серии ЗОПрУ вычисляются экстремальные (по возможности все локальные) значения некоторой фазовой координаты при фиксированных значениях для всех остальных координат. В контексте схемы оптимизации позиционного управления узлы, представляющие содержание множества W[tj], могут быть введены условно, так как при работе оптимизационного алгоритма в случае несвязности множества достижимости будут удалены такие элементы множества Итак, для эффективной реализации схемы необходимо учитывать возможности несвязности, вырождения в многообразие меньшей размерности для множества достижимости. Для аппроксимации, скажем, трехмерного множества достижимости его двухмерные сечения необязательно строить также методом сечений: можно применить для упрощения расчетов, к примеру, метод опорных гиперплоскостей в предположении выпуклости этих плоских сечений. Разработанная компьютерная программа позволяет строить аппроксимации множеств достижимости. В основе лежат программы для численной оптимизации программных управлений в системах с фазовыми ограничениями. Рассмотрим пример аппроксимации контура невыпуклого множества разрешимости. Рассматривается система, описывающая управление с помощью p(t) плоским маятником в среде с неизвестной вязкостью q(t) (управление второго игрока) на отрезке времени [0, 2]:
На управления наложены ограничения:
Основным отличием методов сечений и опорных гиперплоскостей от методов эллипсоидов и других является вычисление аппроксимации множества достижимости, исходя непосредственно из определения этого множества. Для нахождения семейства оптимальных программных управлений, аппроксимирующих оптимальное позиционное управление на частичном временном отрезке [tj, tj+1] (
относительно системы (1)–(7) при поточечных фазовых ограничениях и краевых условиях На отрезке [tS, tF] проводится вычисление оптимального позиционного управления последовательно, переходя от отрезка [tN-1, tN] к отрезку [t0, t1], на основе принципа оптимальности Беллмана. Для каждой позиции {tj, xj(tj)},
В узлах сетки
Функция цены управляющего параметра Функция Беллмана на множестве W[tj] и ее аппроксимация как объединение всех наименьших значений функции цены по всем элементам множества
где На отрезке [tj, tj+1] (
Приведенная схема реализована программно, причем в случае аппроксимации позиционного управления семействами программных управляющих функций требуется привлечение программных средств для оптимизации программных управлений вместо простой схемы выбора значений параметра, изложенной ранее. Случай аппроксимации параметрами более простой и менее трудоемкий, поэтому с точки зрения сравнительной эффективности можно считать его наиболее приемлемым. По результатам работы алгоритмов, реализующих изложенную схему, строится композиционное программное управление, обеспечивающее кусочно-дифференцируемую траекторию, по которой производится перевод системы на целевое множество. Если реализуется случай аппроксимации позиционного управления семействами параметров, то может понадобиться сглаживание получаемой траектории. С этой целью проводится приближение композиционного управления как кусочно-постоянной функции полиномиальной функции достаточно высокой степени. Таким образом, итоговым этапом работы программной системы является применение результатов, насчитанных для всех аппроксимирующих сечений трубки разрешимости, для построения оптимального программного движения из любой позиции, взятой из аппроксимации этой трубки, на целевое множество. Вопросы численной оптимизации программных управлений Как уже отмечено, элементарной операцией в алгоритмах аппроксимации множеств разрешимости и оптимизации позиционного управления является ЗОПрУ, которая может оказаться достаточно трудноразрешимой. Эффективность решения серии ЗОПрУ зависит от уровня надежности (включая уровень автоматизации) программного обеспечения. Авторами проведена реализация (на языке Fortran) ряда методов улучшения программных управлений. На языке Maple разработана программа автоматического вывода конструкций принципа максимума Понтрягина и его линеаризованной версии. Для учета концевых и поточечных фазовых ограничений реализованы методы гладких и недифференцируемых по Фреше штрафных функционалов. Разработанная технология решения ЗОПзУ и аппроксимации множеств разрешимости не используют дифференциальное уравнение Гамильтона–Якоби–Беллмана, опираются непосредственно на определение множеств разрешимости и принцип оптимальности Беллмана, реализуемый на аппроксимации трубки разрешимости. В подходе элементарной операцией является ЗОПрУ, следовательно, эффективность его зависит от эффективности методов и многометодных схем решения ЗОПрУ. Таким образом, аппарат аппроксимации траекторных трубок, а также решения ЗОПрУ и ЗОПзУ является единым с точки зрения достаточно полного исследования возможностей управления в нелинейных дифференциальных системах. Литература 1. Моисеев Н.Н. Численные методы в теории оптимальных систем. М.: Наука, 1971. 2. Моржин О.В., Тятюшкин А.И. Алгоритм метода сечений и программные средства для построения множеств достижимости // Изв. РАН. Теория и системы управления. 2008. № 1. С. 5–11. 3. Тятюшкин А.И., Моржин О.В. Алгоритм численного синтеза оптимального управления // Автоматика и телемеханика. 2008. № 4. 4. Тятюшкин А.И., Моржин О.В. Конструктивные методы оптимизации управлений в нелинейных системах // Там же. 2009. № 4. |
| Permanent link: http://swsys.ru/index.php?id=2258&lang=en&page=article |
Print version Full issue in PDF (4.72Mb) |
| The article was published in issue no. № 2, 2009 |
Perhaps, you might be interested in the following articles of similar topics:
- Прогнозирование на основе выделения границы реализаций динамических систем
- Реберная раскраска кубического графа в задаче распараллеливания расчетов на неструктурированной поверхностной расчетной сетке
- Численная оптимизация настроек регуляторов с учетом колебательности
- Моделирование аттрактора Лоренца
Back to the list of articles
 ,
,  ,
, 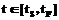 , (1)
, (1) ,
,
 , где компакт X определяется в контексте конкретной задачи управления.
, где компакт X определяется в контексте конкретной задачи управления. .
. , для системы (1) в момент
, для системы (1) в момент  при заданном целевом множестве M называется множество, состоящее из всевозможных состояний в момент t=t, из которых система переводима на M при любых управлениях
при заданном целевом множестве M называется множество, состоящее из всевозможных состояний в момент t=t, из которых система переводима на M при любых управлениях  .
. , системы (1) на полуотрезке [tI, tII) (tS≤tI.
, системы (1) на полуотрезке [tI, tII) (tS≤tI. ,
,  ,
,  , являются дополнительными критериями качества управления, которое, если удовлетворяет ограничениям, называется допустимым. При фазовых ограничениях речь идет об условных множествах достижимости и разрешимости, для аппроксимации которых недостаточно отсечения частей соответствующих множеств системы без фазовых ограничений. Обозначим условные и безусловные множества одинаково, так как из контекста ясен смысл обозначений.
, являются дополнительными критериями качества управления, которое, если удовлетворяет ограничениям, называется допустимым. При фазовых ограничениях речь идет об условных множествах достижимости и разрешимости, для аппроксимации которых недостаточно отсечения частей соответствующих множеств системы без фазовых ограничений. Обозначим условные и безусловные множества одинаково, так как из контекста ясен смысл обозначений. .
. , определяющую управление системой для каждой позиции {t, x} из трубки разрешимости.
, определяющую управление системой для каждой позиции {t, x} из трубки разрешимости. : 0=t0< .
: 0=t0< . которой следуют по узлам tj:
которой следуют по узлам tj:  …,
…,  , …,
, …,  . Для краткости вместо W(tj, tF, M) будем писать W[tj].
. Для краткости вместо W(tj, tF, M) будем писать W[tj]. , будем называть такое конечное множество
, будем называть такое конечное множество  ,
,  , что справедлива формула
, что справедлива формула


 , где q(tj) означает количество элементов во множестве
, где q(tj) означает количество элементов во множестве  , квантор
, квантор  имеет смысл «почти для всех».
имеет смысл «почти для всех».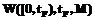 системы, рассматриваемой на отрезке [0, tF], называется конечное множество
системы, рассматриваемой на отрезке [0, tF], называется конечное множество 
 ,
,  с условием 0
с условием 0 ,
, .
. ,
,  ,
,  . Целевое множество M=(0, 0). Положим функцию q(t)=0.5 и для построения контура множества W(0, 2, M) рассмотрим систему в обратном времени, полагая за начальный момент t=0:
. Целевое множество M=(0, 0). Положим функцию q(t)=0.5 и для построения контура множества W(0, 2, M) рассмотрим систему в обратном времени, полагая за начальный момент t=0: ,
, ,
,  ), проводится решение серии ЗОПрУ с целевым крите- рием
), проводится решение серии ЗОПрУ с целевым крите- рием ,
,  ,
, ,
,  .
. , определяется программное управление для движения на текущем частичном временном отрезке [tj, tj+1]. Тем самым проводится аппроксимация позиционного управления программными управлениями – функциями или параметрами. Для простоты изложения ограничимся случаем аппроксимации параметрами.
, определяется программное управление для движения на текущем частичном временном отрезке [tj, tj+1]. Тем самым проводится аппроксимация позиционного управления программными управлениями – функциями или параметрами. Для простоты изложения ограничимся случаем аппроксимации параметрами. Условие
Условие  , где
, где  – заданный числовой вектор,
– заданный числовой вектор,  ,
,  , b≥1.
, b≥1. функция цены j позиционного управления u(t, x) принимает лишь нулевые значения. Рассмотрим функцию
функция цены j позиционного управления u(t, x) принимает лишь нулевые значения. Рассмотрим функцию , tÎ[tj, tj+1].
, tÎ[tj, tj+1]. для позиции
для позиции  :
:  ,
,  . Для позиции
. Для позиции  (
( и соответствующих значений функции цены на последующих частичных временных отрезках.
и соответствующих значений функции цены на последующих частичных временных отрезках.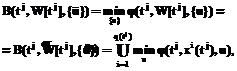
 – объединение оптимальных программных управлений по всем узлам из
– объединение оптимальных программных управлений по всем узлам из  .
. (
( , во-первых, оптимального программного управления
, во-первых, оптимального программного управления  и, во-вторых, управления
и, во-вторых, управления  , на котором достигается максимальное значение функции цены, а также вычисление значений функций B и jmax:
, на котором достигается максимальное значение функции цены, а также вычисление значений функций B и jmax:



 ,
,  .
.