Journal influence
Bookmark
Next issue
The morphological and typological analysis of structures transport knot
The article was published in issue no. № 3, 2009Abstract:In work the information-statistical approach of the morphological and typological analysis of structures transport is considered.
Аннотация:В работе рассматривается информационно-статистический подход морфологического и типологического анализа структур транспортных узлов.
| Authors: Klavdiev A.A. (kss59@mail.ru) - National Mineral Resources University (University of Mines), St. Petersburg, Russia, Ph.D | |
| Keywords: an extreme principle, the information-statistical approach, the uncertainty factor, polycriteriational problem statement |
|
| Page views: 9884 |
Print version Full issue in PDF (4.21Mb) |
Важной особенностью транспортных узлов является широкое разнообразие количественных и качественных характеристик, что обусловливает необходимость проведения морфологического и типологического анализа их качества с целью формирования наиболее объективного мнения о процессах создания и развития узлов. Метод морфологического анализа в сочетании с типологическим анализом ориентирован на решение задачи многовариантной сравнительной оценки объектов в многокритериальной постановке с учетом объективно существующих факторов неопределенности и уровня информационной обеспеченности. В наиболее общем виде такая задача укладывается в следующую схему. Имеется m сравниваемых между собой объектов (транспортных узлов) – O1, О2, …, Оi, …, Оm, которым может быть поставлен в соответствие ряд показателей П1, П2, …, Пj, …, Пn, определяющих предпочтительность того или иного объекта. Предпочтительность объекта Оi с позиции учета одного показателя Пj может быть определена показателем Xji, имеющим определенный физический смысл (объем хранимых фиксированных грузовых единиц, время перегрузки, время простоя и др.). Для некоторых критериев сравнения предпочтительность объектов может быть определена рангом (порядковым номером, который получает каждый объект при расстановке их в порядке предпочтения с позиции рассматриваемого критерия), числом баллов или качественным показателем (отношением порядка предпочтения в виде О1ý О2ý …). В формализованном виде исходная информационная ситуация может быть представлена следующей морфологической матрицей:
Так как для сравнительного анализа привлекается ограниченная совокупность объектов одного типа (выборка), то в общем случае набор оценок показателей Xji (i=1, …, m, j=1, …, n) является выборкой случайных величин, законы распределения которых неизвестны. Неизвестными являются и веса критериев Пj(rj, Если считать, что проблема оценки весов более или менее удовлетворительно преодолена, а исходная морфологическая матрица преобразована в матрицу с однородными элементами Pji, имеющими один и тот же вероятностный смысл, определяющий рейтинг показателя объектов, то вполне естественным является введение в качестве обобщенного показателя (оценочного функционала), позволяющего произвести ранжирование сравниваемых объектов (критерия Байеса):
Используя показатель (1), можно определить комплексный критерий, установить порядок предпочтения в ранжированном виде всех объектов и дать вероятностную интерпретацию полученному решению. Тогда информационная ситуация может быть представлена в виде следующей матрицы:
Таким образом, при постановке и решении рассматриваемой задачи представляется целесообразным выделить следующие этапы: 1) формирование матрицы показателей и результатов оценки предпочтительности объектов по совокупности характеристик и критериев сравнивания; 2) преобразование качественных показателей в количественные; 3) преобразование коррелированных значений показателей в некоррелированные; 4) преобразование элементов матрицы к безразмерному (стьюдентизированному) виду и определение вероятностных мер, соответствующих этим элементам; 5) разработка моделей расчета коэффициентов весомости для сравниваемых показателей; 6) проведение расчетов и анализа обобщенных (комплексных) показателей, характеризующих каждый объект; вероятностная и смысловая интерпретация результатов анализа. В тех случаях, когда для некоторых критериев предпочтительность объектов определена на качественном (или полукачественном) уровне с помощью ранговых оценок или баллов, целесообразно использовать принцип максимума неопределенности [1], количественная оценка показателя Рij (индекс j для дальнейших выводов и рассуждений опустим) в этом случае может быть представлена в виде
где Справедливость зависимости (2) вытекает из решения следующей экстремальной задачи:
где H2(P2) – мера неопределенности второго рода. Для иллюстрации такого подхода рассмотрим следующий пример. Пусть по критерию Пn определено, что объект O1 предпочтительнее объекта О2, а О2 предпочтительнее всех остальных. Символически это может быть записано следующим образом: Предполагается, что объекты O3, О4, …, Оm с точки зрения оценки их по критерию Пn являются равнозначными. Требуется определить значения показателей Рni. Определение показателей Рni в этом случае сводится к решению экстремальной задачи (3):
Введем неопределенный множитель и составим функцию Лагранжа:
Экстремум меры неопределенности Н2 достигается при условии, что
Если умножить полученные уравнения последовательно на Р1, Р2, Р3 и просуммировать их, можно определить множитель l следующим образом: Последовательно подставляя последнее выражение в частные производные функции Лагранжа, после сокращений и преобразований находим:
Нетрудно заметить, что прямое решение экстремальной задачи для конкретного случая наглядно иллюстрирует предлагаемый подход и не вызывает принципиальных затруднений. Следует учитывать, что в частном случае для простого отношения предпочтения оценки вида (2) вырождаются в так называемые оценки Фишборна [2]. Отметим также, что предлагаемый информационно-статистический подход к проблеме морфологического и типологического анализа объектов восприимчив к априорной информации, представленной в различных видах, в том числе полученной в результате экспертного анализа факторов, определяющих предпочтительность характеристик транспортных узлов. Литература 1. Мартыщенко Л.А., Филюстин А.Е., Голик Е.С., Клавдиев А.А. Военно-научные исследования и разработка вооружения и военной техники. СПб: МО РФ, 1993. Ч. I. 302 с. 2. Мартыщенко Л.А., Ивченко Б.П., Монастырский М.Л. Теоретические основы информационно-статистического анализа сложных систем. СПб: Лань, 1997. 320 с. |
| Permanent link: http://swsys.ru/index.php?id=2327&lang=en&page=article |
Print version Full issue in PDF (4.21Mb) |
| The article was published in issue no. № 3, 2009 |
Back to the list of articles
 =1). Заметим, что определение весовых коэффициентов является сложным элементом в рассматриваемой задаче и требует использования соответствующих рабочих гипотез, на основе которых методами теории принятия решений в условиях неопределенности могут быть построены модели весовых коэффициентов. Введем в рассмотрение и используем некоторые модели расчета весовых коэффициентов, адекватных рассматриваемой проблеме.
=1). Заметим, что определение весовых коэффициентов является сложным элементом в рассматриваемой задаче и требует использования соответствующих рабочих гипотез, на основе которых методами теории принятия решений в условиях неопределенности могут быть построены модели весовых коэффициентов. Введем в рассмотрение и используем некоторые модели расчета весовых коэффициентов, адекватных рассматриваемой проблеме. . (1)
. (1) (2)
(2) ,
,  , i – порядковый номер предпочтения объекта в общей совокупности, определяемый или по отношению порядка предпочтения (см. последнюю строку исходной матрицы), или по баллам, или по ранговой последовательности; ai – степень кратности порядковых номеров k.
, i – порядковый номер предпочтения объекта в общей совокупности, определяемый или по отношению порядка предпочтения (см. последнюю строку исходной матрицы), или по баллам, или по ранговой последовательности; ai – степень кратности порядковых номеров k. , (3)
, (3) ,
, .
. .
. .
.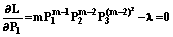 ,
, ,
, .
. .
. ,
, 
 ,
, .
.