Существует немало программных продуктов, позволяющих прогнозировать процесс эпидемии, строить динамику распространения инфекции в однородном сообществе, зная начальные данные и интенсивность управления. Данный программный продукт в отличие от предыдущих учитывает три различных вида управления, направленных на погашение инфекции сразу в n различных группах.
Рассмотрим динамику управляемого процесса распространения эпидемии в неоднородном сообществе, состоящем из n возрастных групп, в виде следующей системы дифференциальных уравнений:
 (1)
(1)
 ,
, 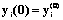 ,
,
 ,
,  ,
,  , (2)
, (2)
где  и
и  – число подверженных заболеванию и инфицированных в i-й группе (i=1, …, n) в момент t;
– число подверженных заболеванию и инфицированных в i-й группе (i=1, …, n) в момент t;  – функция, характеризующая скорость заражения подверженных заболеванию из i-й группы от инфицированных из j-й группы с вероятностью
– функция, характеризующая скорость заражения подверженных заболеванию из i-й группы от инфицированных из j-й группы с вероятностью  (
( );
);  – количество людей, восстановивших за единицу времени свое здоровье в i-й группе без воздействия внешних средств: карантина, вакцинации и др. (
– количество людей, восстановивших за единицу времени свое здоровье в i-й группе без воздействия внешних средств: карантина, вакцинации и др. ( – среднее время естественного выздоровления);
– среднее время естественного выздоровления);  – коэффициент естественной смертности людей в i-й группе;
– коэффициент естественной смертности людей в i-й группе;  – коэффициент смертности от данной инфекции в i-й группе;
– коэффициент смертности от данной инфекции в i-й группе;  – средний показатель рождаемости в i-й группе;
– средний показатель рождаемости в i-й группе;  – доля вакцинированных среди подверженных заболеванию в i-й группе;
– доля вакцинированных среди подверженных заболеванию в i-й группе;  – доля больных, отправленных на карантин;
– доля больных, отправленных на карантин;  – доля людей, подверженных заболеванию, на которых успешно воздействовали с помощью программы «Здоровье».
– доля людей, подверженных заболеванию, на которых успешно воздействовали с помощью программы «Здоровье».
Целью управления является минимизация затрат на погашение эпидемии, выраженных функционалом:

 , (3)
, (3)
где A – средняя стоимость одного больного для общества в неделю (известная величина, для России составляет примерно 50 долларов [1]); для одного человека из i-й группы: Di – стоимость вакцинации, Ci – стоимость изоляции, Zi – стоимость программы «Здоровье». Если принять A равным одной условной денежной единице, то (3) перепишется в виде:

 , (4)
, (4)
где di – относительная стоимость вакцинации;  – относительная стоимость программы «Здоровье»; ci – относительная стоимость карантина в i-й группе.
– относительная стоимость программы «Здоровье»; ci – относительная стоимость карантина в i-й группе.
Ограничения на функцию управления заданы в следующем виде:
 , (5)
, (5)
где Аi, Вi, Ci – максимальные нормы управлений в i-й группе, ограниченные техническими и материальными возможностями.
Разобьем отрезок интегрирования [0; T] на q равных частей точками  так, что
так, что 
 . Задача (1)–(5) аппроксимируется следующей дискретной задачей оптимального управления:
. Задача (1)–(5) аппроксимируется следующей дискретной задачей оптимального управления:
 , (6)
, (6)
 (7)
(7)
где 
 .
.
 (8)
(8)
 ,
,  ,
,
 . (9)
. (9)
 Составим функцию Лагранжа для дискретной задачи, откуда найдем производные лагранжиана по управлениям
Составим функцию Лагранжа для дискретной задачи, откуда найдем производные лагранжиана по управлениям  ,
,  ,
,  и по фазовым переменным, чтобы выразить сопряженные функции:
и по фазовым переменным, чтобы выразить сопряженные функции:
 (10)
(10)
Условия трансверсальности:
 . (11)
. (11)
Алгоритм численного решения
1. Зададим начальное управление

 2. Зададим начальные значения
2. Зададим начальные значения 
 . По формуле (7) вычислим допустимые траектории, по формуле (6) – начальное значение интеграла.
. По формуле (7) вычислим допустимые траектории, по формуле (6) – начальное значение интеграла.
3. Для 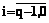 вычислим по формуле (10) с учетом (11)
вычислим по формуле (10) с учетом (11)  ,
, ,
, .
.
4. Вычислим следующее приближение для управления:

 .
.
Проверим условие (9): если оно не выполняется, делаем проекцию градиента:
если 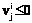 , то
, то  , если
, если  , то
, то 
 ;
;
если  , то
, то 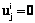 , если
, если  , то
, то 
 ;
;
если  , то
, то  , если
, если  , то
, то 
 .
.
5. По формуле (7) вычислим допустимые траектории  , по формуле (6) – следующее значение интеграла
, по формуле (6) – следующее значение интеграла  .
.
6. Сравним значения  и
и  . Если
. Если  , переходим к пункту 3, присвоив
, переходим к пункту 3, присвоив  найденные в пункте 4 значения управлений. Процесс продолжается до тех пор, пока
найденные в пункте 4 значения управлений. Процесс продолжается до тех пор, пока  .
.
7. Если  , возвращаемся к пункту 4 и уменьшаем шаг
, возвращаемся к пункту 4 и уменьшаем шаг  , например в два раза, проверяем условие (9).
, например в два раза, проверяем условие (9).
Для проведения эксперимента на реальной модели были взяты статистические данные по развитию эпидемии гриппа в г. Архангельске, предоставленные Территориальным управлением по эпиднадзору. Рассмотрим четыре возрастные группы: 1-я группа – 0–2 года, 2-я группа – 3–6 лет, 3-я группа – 7–15 лет, 4-я группа – старше 15 лет. Коэффициенты смертности, средний показатель рождаемости для каждой группы вычислены по статистическим данным для г. Архангельска. Коэффициенты β найдены путем решения обратной задачи.
Программа по нахождению оптимального управления написана в среде Delphi7 на языке Object Pascal. Все параметры модели пользователь может вводить с клавиатуры, что позволяет исследовать решение задачи в зависимости от введенных параметров.
 После окончания работы программы искомое значение функции выводится в окно Результат (рис. 1), а графическое решение (фазовые переменные, программное управление, функции переключения управления) по каждой группе можно получить в окне Графики нажатием соответствующей кнопки.
После окончания работы программы искомое значение функции выводится в окно Результат (рис. 1), а графическое решение (фазовые переменные, программное управление, функции переключения управления) по каждой группе можно получить в окне Графики нажатием соответствующей кнопки.
Кроме того, решение дискретной задачи оптимального управления выводится в Excel, что позволяет сравнивать решения задачи при различных параметрах. Наиболее сильное влияние на решение оказывают стоимость управлений, величина временного интервала [0; T] и коэффициенты β. Зафиксировав стоимость изоляции и программы «Здоровье», выявим влияние стоимости вакцинации на решение задачи. Так как изменения во всех группах аналогичные, то для примера выясним, как меняются динамика подверженных заболеванию и управление вакцинацией в 3-й группе (рис. 2), которые сильнее всего зависят от стоимости вакцинации (d1>d2>d3).
Из рисунка видно, что с уменьшением стоимости вакцинации уменьшается остаточное на
момент Т количество подверженных заболеванию, а продолжительность управления растет.
Аналогично можно рассмотреть влияние стоимости изоляции (карантина) на динамику инфицированных и управление изоляцией в 3-й группе (рис. 3), которые сильнее всего зависят от стоимости изоляции (с1>с2>с3).
Программа позволяет исключить отсутствующий вид управления, чтобы проследить эффективность оставшихся видов управления и суммарные затраты на погашение эпидемии. Таким образом, было выяснено, что самым эффективным и дешевым способом управления является комплексное управления вакцинацией, карантином и программой «Здоровье».
Литература
1. Вакцинация. Новости вакцинопрофилактики // Информационный бюллетень. М. 2003. № 3 (27).
2. Андреева Е.А. Оптимальное управление динамическими системами. Тверь: Изд-во ТвГУ, 1999. С. 72–120.
 (1)
(1) ,
, 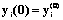 ,
, ,
,  ,
,  , (2)
, (2) и
и  – число подверженных заболеванию и инфицированных в i-й группе (i=1, …, n) в момент t;
– число подверженных заболеванию и инфицированных в i-й группе (i=1, …, n) в момент t;  – функция, характеризующая скорость заражения подверженных заболеванию из i-й группы от инфицированных из j-й группы с вероятностью
– функция, характеризующая скорость заражения подверженных заболеванию из i-й группы от инфицированных из j-й группы с вероятностью  (
( );
);  – количество людей, восстановивших за единицу времени свое здоровье в i-й группе без воздействия внешних средств: карантина, вакцинации и др. (
– количество людей, восстановивших за единицу времени свое здоровье в i-й группе без воздействия внешних средств: карантина, вакцинации и др. ( – среднее время естественного выздоровления);
– среднее время естественного выздоровления);  – коэффициент естественной смертности людей в i-й группе;
– коэффициент естественной смертности людей в i-й группе;  – коэффициент смертности от данной инфекции в i-й группе;
– коэффициент смертности от данной инфекции в i-й группе;  – средний показатель рождаемости в i-й группе;
– средний показатель рождаемости в i-й группе;  – доля вакцинированных среди подверженных заболеванию в i-й группе;
– доля вакцинированных среди подверженных заболеванию в i-й группе;  – доля больных, отправленных на карантин;
– доля больных, отправленных на карантин;  – доля людей, подверженных заболеванию, на которых успешно воздействовали с помощью программы «Здоровье».
– доля людей, подверженных заболеванию, на которых успешно воздействовали с помощью программы «Здоровье».
 , (3)
, (3)
 , (4)
, (4) – относительная стоимость программы «Здоровье»; ci – относительная стоимость карантина в i-й группе.
– относительная стоимость программы «Здоровье»; ci – относительная стоимость карантина в i-й группе. , (5)
, (5) так, что
так, что 
 . Задача (1)–(5) аппроксимируется следующей дискретной задачей оптимального управления:
. Задача (1)–(5) аппроксимируется следующей дискретной задачей оптимального управления: , (6)
, (6) (7)
(7)
 .
. (8)
(8) ,
,  ,
, . (9)
. (9) Составим функцию Лагранжа для дискретной задачи, откуда найдем производные лагранжиана по управлениям
Составим функцию Лагранжа для дискретной задачи, откуда найдем производные лагранжиана по управлениям  ,
,  ,
,  и по фазовым переменным, чтобы выразить сопряженные функции:
и по фазовым переменным, чтобы выразить сопряженные функции: (10)
(10) . (11)
. (11)


 . По формуле (7) вычислим допустимые траектории, по формуле (6) – начальное значение интеграла.
. По формуле (7) вычислим допустимые траектории, по формуле (6) – начальное значение интеграла.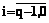 вычислим по формуле (10) с учетом (11)
вычислим по формуле (10) с учетом (11)  ,
, ,
, .
.
 .
.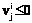 , то
, то  , если
, если  , то
, то 
 , то
, то 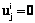 , если
, если  , то
, то 
 , то
, то  , если
, если  , то
, то 
 , по формуле (6) – следующее значение интеграла
, по формуле (6) – следующее значение интеграла  .
. и
и  , переходим к пункту 3, присвоив
, переходим к пункту 3, присвоив  найденные в пункте 4 значения управлений. Процесс продолжается до тех пор, пока
найденные в пункте 4 значения управлений. Процесс продолжается до тех пор, пока  .
. , возвращаемся к пункту 4 и уменьшаем шаг
, возвращаемся к пункту 4 и уменьшаем шаг  , например в два раза, проверяем условие (9).
, например в два раза, проверяем условие (9).
