Software & Systems

Задача поиска маршрута для транспортных средств с ограничением по времени относится к широко распространенному классу задач. Для ее решения используется множество методов: генетические алгоритмы [1], муравьиный алгоритм [2], различные эвристические алгоритмы [3], программирование с ограничениями [4]. В данной статье описывается генетический алгоритм, использующий оригинальные алгоритмы в своих операторах и эффективно решающий транспортные задачи с ограничениями по времени.

Постановка задачи

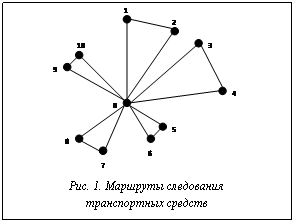Транспортная задача с ограничением по времени описывается следующим образом. Имеются некоторое количество транспортных средств, один склад (депо) и некоторое количество клиентов [1]. Задача заключается в поиске эффективного маршрута для транспортных средств, обслуживающих определенное количество клиентов. При этом все маршруты должны начинаться и заканчиваться в депо. Рисунок 1 иллюстрирует пример такого маршрута. Точка 0 – депо, точки 1–10 – клиенты.

Для данной задачи определены цели (в порядке убывания их приоритета).

1. Минимизировать общее количество транспортных средств (V – количество идентичных автомобилей грузоподъемностью q), необходимых для удовлетворения всех потребностей клиентов.

2. Минимизировать общее время обслуживания всех клиентов: .

3. Минимизировать общее расстояние, пройденное всеми транспортными средствами.

На маршруты накладываются следующие ограничения [1]:

 – каждый клиент должен быть обслужен только одним транспортным средством. Переменные Xijk принимают значения {0, 1}. В данном случае 1 означает, что автомобиль движется от вершины i к вершине j, 0 – обратное. Верхним индексом k обозначается соответствующий автомобиль, где kÎV;

 – транспортное средство не может обслужить больше клиентов, чем позволяет его грузоподъемность di, где iÎC – спрос соответствующего клиента; C – множество клиентов;

 – ограничение по времени; прибытие автомобиля к клиенту должно быть в пределах временного окна, где Sik – время прибытия соответствующего автомобиля к определенному клиенту; [ai,bi] – промежуток времени, так называемое временное окно (time window), в течение которого должен быть обслужен клиент.

Генетические алгоритмы

Генетические алгоритмы относятся к методам случайного поиска решения задач оптимизации. Они основаны на имитации естественного отбора и природных генетических механизмов [1]. Генетические алгоритмы продемонстрировали значительные успехи при решении многих сложных задач оптимизации. Основными операторами генетических алгоритмов являются инициализация, скрещивание, мутация.

Оператор инициализации генерирует новые цепочки хромосом, которые являются частью общей популяции.

Оператор скрещивания предназначен для получения новых решений на основе тех, что находятся в данный момент в популяции. Он получает на вход две или более хромосом, на выходе выдает комбинированное решение, которое построено на основе входных решений. Самым распространенным видом кроссовера является N-точечный кроссовер (рис. 2).

Оператор мутации предназначен для вывода популяции из локального оптимума. Он получает на вход хромосому и с некоторой вероятностью инвертирует часть ее генов (рис. 3).

Модифицированные операторы генетического алгоритма

Оператор инициализации. Основной задачей модифицированного оператора инициализации является генерация маршрутов таким образом, чтобы они были корректны (см. условия в описании задачи), а также минимизировать путь, пройденный каждой машиной. Для обеспечения этого применяется алгоритм, изображенный на рисунке 4.

Описание элементов блок-схемы.

1. Переменные: N – вектор, содержащий номера клиентов; K – вектор координат пунктов на карте; D – вектор потребностей каждого клиента; CP – вместимость каждого транспортного средства; P, r – локальные переменные.

2.   Происходит кластеризация пунктов методом k-средних по географическому признаку. В результате в одном кластере окажутся точки, расстояние между которыми минимально.

3.   Выполняется итерация по каждому класс- теру.

4.   В p содержится i-й кластер.

5.   Если размер кластера равен нулю, цикл прерывается.

6.   В е размещается случайный элемент кластера p, при этом сам элемент удаляется из него.

7.   Проверяется суммарная потребность клиентов, входящих в маршрут r, если она больше, пункт e невозможно добавить в текущий марш- рут r.

8.   Пункт e либо добавляется в текущий маршрут, либо помещается обратно в кластер, которому принадлежал (в зависимости от шага 7).

9.   Если суммарная потребность в пунктах в новом маршруте r больше или равна суммарной потребности в пунктах, оставшихся в текущем кластере, то повторить цикл.

10.  Последним элементом вектора, содержащего маршрут, добавляют время старта данного транспортного средства, исходя из того, что оно может быть в пределах от 0 до 24*60 минут.

Оператор мутации. Задачей оператора мутации является изменение хромосомы таким образом, чтобы не нарушить выполнение условий 1 и 2 из целей задачи. Для этого маршруты по очереди подвергаются мутации. Для каждого маршрута оператор выполняет перестановку пунктов назначений, входящих в маршрут (рис. 5). Из рисунка видно, что изменился только порядок обслуживания клиентов с номерами 3 и 7.

Оператор скрещива­ния. Он работает таким образом, чтобы не только получить новые маршруты, но и уменьшить их число, сократив тем самым количество транспортных средств. Для этого применяется алгоритм, приведенный на рисунке 6.

Описание элементов блок-схемы.

1.   Входные параметры оператора скрещивания: F, M – пара родительских хромосом; E –локальная переменная, хранящая один маршрут; r – результат объединения родительских хромосом.

2.   Объединяет маршруты, содержащиеся в обеих родительских хромосомах. Получается карта маршрутов, в которой некоторые пункты посещались 1 или 2 раза.

3.   Цикл выполняется до тех пор, пока в объединенном маршруте N есть хоть один маршрут.

4.   В S помещается один из маршрутов, содержащихся в N, при этом сам маршрут удаляется из N.

5.   Цикл выполняется для каждого пункта, находящегося в маршруте S.

6.   Если текущий элемент S[i] уже содержится в результирующем маршруте, он пропускается.

7.   Выбирается маршрут из r, в котором суммарная потребность клиентов меньше, чем в переданном клиенте с номером S[i].

8.   Если такой клиент найден, то k будет содержать индекс его маршрута в r.

9.   Добавляем текущий пункт либо в r[k], либо в E, если нет маршрута, удовлетворяющего условию.

10.     В r будет добавлен маршрут, содержащий точки, которые не удалось добавить ни в один из существующих маршрутов.

Результаты тестирования

Тестирование проводилось на тестовых задачах Соломона [5]. Тестовые задачи разделены на классы:

·     R – клиенты географически распределены равномерно вероятностным образом;

·     C – клиенты расположены группами;

·     RC – часть клиентов расположена группами, а остальные распределены равномерно вероятностным образом.

В каждой задаче 100 клиентов, депо (пункт назначения под номером 1), максимальная грузоподъемность транспортного средства. В таблице приведено сравнение работы алгоритма с лучшими решениями.

Из таблицы видно, что предлагаемый в данной статье алгоритм превосходит по количеству необходимых машин лучшие результаты, но проигрывает по пройденному расстоянию.

Следовательно, данный алгоритм позволяет эффективно решать транспортные задачи с ограничением по времени.

Литература

1.   Емельянова Т.С. Решение эталонных транспортных задач с кластерным расположением клиентов с использованием генетических алгоритмов // Нечеткие системы и мягкие вычисления (НСМВ-2008) : сб. науч. тр. Второй Всеросс. науч. конф. с междунар. участ. Т. 1. 2008. С. 195–199.

2.   Vladimir Vacic and Tarek M. Sobh. Routing Problem with Time Windows. Department of Computer Science and Engineering University of Bridgeport, Bridgeport, USA. 2002. URL: vladi­mir@vacic.org, sobh@bridgeport.eduVehicle (дата обращения: 20.03.2009).

3.   Roberto De Franceschi,Matteo Fischetti,Paolo Toth.A new ILP-based refinement heuristic for Vehicle Routing Problems. 2004.

4.   Paul Shaw. Using Constraint Programming and Local Search Methods to Solve Vehicle Routing Problems. Department of Computer Science, University of Strathclyde, Glasgow. April 1998.

5.   URL: http://web.cba.neu.edu/~msolomon/heuristi.htm (дата обращения: 20.03.2009).