Journal influence
Bookmark
Next issue
Application of unified program modules at development of training systems
The article was published in issue no. № 4, 2009Abstract:Problem of development of special program maintenance of training systems on basis of unified program modules is considered. Models of optimization of special software on criterion of minimum of redundancy of program modules are formulated. Mathematical models of unification of program modules are formulated.
Аннотация:Рассмотрена проблема разработки специального программного обеспечения тренажерных систем на основе унифицированных программных модулей. Сформулированы модели оптимизации специального программного обеспечения по критерию минимума избыточности программных модулей. Сформулированы математические модели унификации программных модулей.
| Authors: (alexandr_prv@rambler.ru) - , Ph.D | |
| Keywords: problem of unification of program modules, synthesis of optimum standard modules, unified program module, special software, training system |
|
| Page views: 9624 |
Print version Full issue in PDF (4.85Mb) |
Одной из задач при проектировании тренажерных систем (ТС) является разработка специального программного обеспечения (СПО). На основе анализа процессов, протекающих в подсистеме вычислительных средств (ВС) ТС при проведении тренировок, можно выделить следующие задачи СПО: · математическое моделирование функций управления специалистов, реакции управляемой системы, динамики, бортовых систем и условий функционирования управляемых объектов; · организация управления параллельно проводимых тренировок на базе ТС. К СПО следует отнести программы, обеспечивающие выполнение задач ВС ТС (планирование ресурсов ТС, реконфигурация вычислительной системы, организация новых тренировок, ведение информационной базы ТС и т.д.). В ТС предъявляются высокие требования к программной устойчивости при искажениях информации, сбоях и частичных отказах аппаратуры, возникающих в процессе ее функционирования. Для решения этой проблемы разрабатываются различные методы резервирования, оперативного и функционального контроля и т.д. Это предполагает построение рациональной структуры системы математического обеспечения, осуществляющей оптимизацию структуры алгоритмов с точки зрения как максимального использования ресурсов ЭВМ, так и эффективности проектирования алгоритмов (иерархичность структуры, разбиение на подпрограммы, унификация подпрограмм решения типовых задач и т.д.). Существуют два подхода к созданию СПО тренажеров. При разработке программ относительно небольшого объема преобладает индивидуальный подход. Основная цель разработчиков состоит в получении результатов при минимальных собственных затратах, однако при этом практически не решаются вопросы оптимизации программ по затратам технических ресурсов ЭВМ, зачастую созданная программа используется только самим разработчиком. Сопряжение такой программы с другими для решения новых комплексных задач и модернизация программы практически невозможны без личного участия ее разработчиков. Другой подход к созданию СПО базируется на представлении программного обеспечения как совокупности унифицированных программных модулей (УПМ). В этом случае комплекс функциональных программ может быть разделен на множество достаточно автономных подсистем – УПМ, тесно взаимодействующих в процессе решения общей задачи. Для обеспечения взаимодействия подпрограмм в едином комплексе широко используется иерархическая структура с несколькими уровнями подчиненности подпрограмм, при этом каждая подпрограмма выполняет свою целевую задачу. Следует учитывать, что при использовании модульного программирования в отдельных подпрограммах появляются элементы сопряжения и взаимодействия блоков, которые требуют определенных затрат оперативной памяти и времени. Дополнительные затраты памяти составляют 2–5 % от объема сопрягаемых подпрограмм, а длительность исполнения программ при этом возрастает на 10–15 %. Анализ особенностей ТС позволяет сделать вывод о перспективности модульного принципа при построении СПО ТС [1]. Сложность объектов моделирования неизбежно приводит к необходимости их функционально-структурной декомпозиции и представления в виде системы достаточно простых элементов-модулей. К тому же сам реальный объект функционально и структурно представляет, как правило, достаточно сложную систему, состоящую из иерархически упорядоченных подсистем, устройств, блоков и элементов. Вполне естественно поставить в соответствие отдельным системам, подсистемам, устройствам реального объекта их адекватные модели – программные модули (ПМ) СПО. Если в разных объектах используются одинаковые устройства или системы, для их моделирования могут использоваться одни и те же модули программ. При создании УПМ с целью использования для различных ТС неизбежно возникает проблема избыточности процедур в модулях, обусловленная стремлением сделать их в определенной степени универсальными. Для определения рациональной степени избыточности сформулируем задачи синтеза оптимальных типовых модулей. В качестве исходной информации для решения подобных задач используются множество процедур обработки данных для каждой ВС ТС, информационных элементов, области их определения, множество констант, структурированные матрицы смежности и достижимости технологии обработки данных. При анализе совокупности задач обработки данных для определения степени их общности и специфичности введено понятие классов их эквивалентности, соответствующее различным степеням важности. Чем выше класс эквивалентности, тем выше степень близости или однородности анализируемых задач (алгоритмов). Наивысший класс эквивалентности задач предполагает совпадение исходных, промежуточных и выходных данных, а также множеств процедур обработки данных и динамических характеристик алгоритмов решения задач, то есть совпадение всех элементов, описывающих задачу. Сравнение алгоритмов решения задач для ВС ТС и выделение в них совпадающих или эквивалентных частей без учета различия в константах и областях определения информационных элементов заключается в определении пересекающихся частей для всего множества задач обработки данных и его подмножеств. Решение данной задачи можно разбить на четыре этапа [2]. На первом этапе определяются множества общих процедур и информационных элементов, используемых в множестве задач обработки данных или в его подмножествах. Одновременно определяются специфические элементы и процедуры, используемые только в одной из задач обработки данных. На втором этапе проверяется связность выделенных общих информационных элементов и процедур обработки данных в графе технологии каждой задачи для различных ВС ТС. Несвязные информационные элементы и процедуры исключаются из дальнейшего рассмотрения. На третьем этапе выделяются общие пути для всего множества задач и его подмножеств, на четвертом определяются общие части (подграфы) для множества задач обработки данных и его подмножеств. Исходные данные для постановки и решения данного типа: Задача 1. Оптимизация СПО ВС ТС по критерию минимума суммарного числа неиспользуемых процедур при обращениях к программным модулям при решении заданного множества задач:
Задача 2. Оптимизация СПО ВС ТС по критерию минимума максимально возможного суммарного числа неработающих процедур в программных модулях для заданного множества задач обработки данных:
Ограничения для данной задачи такие же, что и для задачи распределения процедур по модулям. Использование минимаксных критериев обеспечивает гарантированный уровень качества синтеза для каждой из задач обработки данных заданного множества за счет минимизации максимальных значений рассматриваемых критериев синтеза. Необходимость обеспечения гарантированного уровня качества проектных решений для всех задач обработки данных из заданного множества определяет целесообразность использования такого подхода. Рассмотренные задачи являются нелинейными целочисленными задачами математического программирования. По своим формулировкам, исходным данным, используемым переменным и математическим выражениям они достаточно близки к задаче синтеза оптимального состава модулей и массивов для заданных требований конкрет- ной ВС ТС. Существенное отличие поставленных задач, определяющее их повышенную сложность и размерность, заключается в необходимости получить в определенном смысле оптимальное решение для множества требований различных ВС ТС. При разработке СПО используются не только вновь разрабатываемые ПМ, но и уже имеющиеся, применявшиеся в более ранних разработках ТС. Таких ПМ, выполняющих определенные функции, большое количество. Причем многие из них выполняют сходные функции или часть функций, которые могут реализовывать другие ПМ. Возникает задача определения такого минимального унифицированного ряда ПМ, которые могли бы обеспечить функционирование любого нового ТС (возможно, с некоторой модификацией или избыточностью). Это направлено, в первую очередь, на сокращение времени на разработку и реализацию нового СПО и уменьшение финансовых затрат на всех стадиях жизненного цикла (ЖЦ) СПО. Технология подготовки данных и решения задач унификации ПМ включает математические модели, методы и программы решения задач унификации. Одноуровневые задачи решаются в случае унификации ПМ ВС ТС специального назначения одного вида, имеющихся или разрабатываемых, отличающихся между собой некоторыми характеристиками. Технологическая схема подготовки данных и решения одноуровневой задачи приведена на рисунке 1. Задача может быть сформулирована как задача целочисленного линейного программирования с булевыми переменными, в которой необходимо минимизировать суммарные затраты на разработку, реализацию и сопровождение ПМ.
при ограничениях
где U={1,2,…,m} – множество типов ПМ; xij=
Задача (3)–(6) относится к классу целочисленного линейного программирования с булевыми переменными и является статической задачей унификации с детерминированным спросом на изделия (ПМ) и однократным применением изделия (ПМ) в операционном цикле. Ограничения (4) устанавливают факт возможности применения только одного типа ПМ для решения некоторых видов задач из заданного множества U при условии, что оптимальный ряд типов ПМ обеспечит удовлетворение всех потребностей из множества U. Ограничения (5) следуют из физического смысла параметров оптимизации. К наиболее эффективным методам получения точного решения задачи (3)–(6) относится метод ветвей и границ. Среди известных подходов к формализации алгоритма этого метода выделяется способ, основанный на сведении задачи (3)–(6) к задаче минимизации полинома от булевых переменных. Указанный способ более всего приспособлен для программной реализации алгоритма решения на ЭВМ. Для унификации ПМ, входящих в состав СПО ВС ТС, и самого СПО для использования его в составе ТС можно предложить многоуровневые задачи. В этом случае цель унификации по экономическому критерию заключается в обеспечении функционирования ТС различных версий и модификаций с использованием минимального набора СПО, разработанного с применением минимального набора ПМ. Двухуровневая задача может быть сформулирована следующим образом. Пусть Х={1,2,…n} – множество версий ТС, использующих различное СПО; U={1, 2,…, m} – множество типов ПМ, входящих в состав СПО, применяемого для определенной версии ТС. Будем считать, что комплект СПО, используемый для удовлетворения некоего спроса (обеспечения функционирования различных ТС), может включать в себя разное число ПМ различного типа. Предположим, что комплект рассматриваемого СПО характеризуется значением некоторых К показателей и что для всякого комплекта (q1,q2,…,qm), где число ПМ типа i в данном комплекте (значение показателя k, k=1,…,K, при фиксированном j, jÎX) определяется по значению некоторой функции bkj(q1,…,qm). Считаем, что комплект СПО (q1,q2,…,qm) удовлетворяет ТС номер j, если выполняется соотношение bkj(q1, …,qm)³ ³bkj, k=1,…K, где bkj, k=1,…,K – известные величины. Каждому комплекту ПО можно поставить в соответствие конкретную ТС. Причем количество типов комплектов СПО, отличающихся друг от друга значениями соответствующих показателей, равно количеству типов ТС, в которых они могут применяться. Предположим также, что для всякого iÎU известны величины g0i и ci, означающие, соответственно, начальные затраты на проектирование ПМ типа i и затраты на реализацию одного такого ПМ. Через gj(q) обозначим затраты на сопровождение комплекта СПО (q1,…,qm), где Необходимо формально записать задачу выбора ПМ, позволяющих сформировать комплекты СПО, которые с наименьшими затратами выполнят все функции обеспечения ТС определенного вида. Чтобы вычислить величину суммарных затрат, необходимо знать, из каких типов ПМ состоит комплект СПО, обеспечивающий ТС каждого вида. Введем переменные Понятно также, что если (x1j,…,xmj) – удовлетворяющий ТС j-го вида комплект СПО, то величина затрат, связанных с обеспечением этим комплектом ТС j-го вида, вычисляется по формуле
Однако одних переменных xij еще недостаточно для записи целевой функции, поскольку в ней должен быть отражен факт наличия начальных затрат на создание ПМ каждого типа. Поэтому введем переменные
Рассмотрим частный случай сформулированной задачи, задаваясь функциями Будем считать, что комплект
где Первое ограничение естественно рассматривать как ограничение на число модулей в комплекте СПО, а второе трактовать, например, как ограничение на эффективность комплекта. При этом вид левой части второго ограничения указывает на то, что эффективность комплекта складывается из эффективности входящих в него ПМ:
Технологическая схема подготовки данных и решения двухуровневой задачи унификации приведена на рисунке 2. Двухуровневую задачу унификации можно решить путем комплексного применения метода динамического программирования и метода ветвей и границ. Этот алгоритм предполагает ряд существенных допущений в рассматриваемой задаче. Существует еще один подход – снижение вычислительной сложности за счет декомпозиции двухуровневой задачи на две одноуровневые и применения простых алгоритмов их решения. На верхнем уровне сокращается количество типов ТС, а затем унифицируются ПМ, применяемые в заданных СПО. Динамика потребностей в новых образцах техники приводит к непрерывной замене одних систем другими, что влечет за собой необходимость создания нового СПО для этих систем. Сложившаяся практика, когда вначале осуществляется перспективное планирование развития систем, а затем на основе этих планов предусматриваются работы по унификации, не отвечает современным требованиям. Результаты раздельного решения оптимизационных задач, соответствующих такой схеме, трудно использовать на практике: рекомендации по унификации не всегда являются оптимальными и их подготовка запаздывает относительно сроков разработки изделий. В этом случае сократить номенклатуру уже созданных ПМ крайне сложно, так как она связана с номенклатурой СПО для ВС ТС, находящихся в эксплуатации. Следовательно, необходим комплексный подход к анализу задачи управления процессом поиска рационального соотношения между моментами постановки систем на производство, модификацию, замену существующей версии СПО, и суммарной стоимостью многоуровневых параметрических рядов этих изделий. Литература 1. Привалов А.Н., Милько И.В. Построение программного обеспечения комплексов автоматизации управления войсками и оружием на основе унифицированных программных модулей: науч.-технич. сб. ТАИИ. Тула: ТАИИ, 2003. Вып. 20. С. 54–68. 2. Кульба В.В., Миронов А.С., Товмасян А.В. Формализованные модели предпроектного анализа при разработке модульных СОД: в кн.: Методы анализа и синтеза автоматизированных систем управления. М.: ИПУ, 1981. Вып. 25. С. 30–38. 3. Привалов А.Н., Милько И.В. Основные направления унификации программного обеспечения комплексов автоматизации управления войсками и оружием: науч.-технич. сб. ТАИИ. Тула: ТАИИ, 2003. Вып. 20. С. 46–54. |
| Permanent link: http://swsys.ru/index.php?id=2383&lang=en&page=article |
Print version Full issue in PDF (4.85Mb) |
| The article was published in issue no. № 4, 2009 |
Perhaps, you might be interested in the following articles of similar topics:
 – множество процедур обработки данных интегрированного графа технологии;
– множество процедур обработки данных интегрированного графа технологии;  – множество информационных элементов интегрированного графа технологии;
– множество информационных элементов интегрированного графа технологии;  – множество процедур обработки данных графа технологии i-й задачи;
– множество процедур обработки данных графа технологии i-й задачи;  – множество информационных элементов графа технологии i-й задачи;
– множество информационных элементов графа технологии i-й задачи;  – последовательности выполнения процедур при решении i-й задачи;
– последовательности выполнения процедур при решении i-й задачи;  – матрица взаимосвязей информационных элементов и процедур интегрированного графа технологии;
– матрица взаимосвязей информационных элементов и процедур интегрированного графа технологии;  – матрица взаимосвязей информационных элементов и процедур при решении i-й задачи.
– матрица взаимосвязей информационных элементов и процедур при решении i-й задачи. . (1)
. (1)
 , (2)
, (2)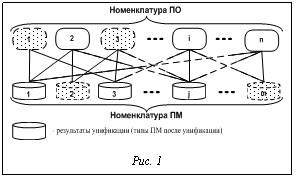 где
где  – множество синтезируемых модулей;
– множество синтезируемых модулей;  , если l-я по порядку выполнения процедура решения i-й задачи входит в v-й модуль и вызывается с частотой k-го диапазона и
, если l-я по порядку выполнения процедура решения i-й задачи входит в v-й модуль и вызывается с частотой k-го диапазона и  в противном случае;
в противном случае;  – значение k-гo диапазона частоты использования процедур при решении i-й задачи.
– значение k-гo диапазона частоты использования процедур при решении i-й задачи. , (3)
, (3) (4)
(4)
 ,
,  ; (5)
; (5) ,
,  , (6)
, (6)

 – вектор начальных затрат на разработку и отладку ПМ i-го типа;
– вектор начальных затрат на разработку и отладку ПМ i-го типа; – матрица затрат на реализацию и сопровождение ПМ i-го типа при применении их в СПО j-го вида; Сij=¥, если ПМ i-го типа не применяются в СПО j-го вида.
– матрица затрат на реализацию и сопровождение ПМ i-го типа при применении их в СПО j-го вида; Сij=¥, если ПМ i-го типа не применяются в СПО j-го вида. при обеспечении этим комплектом j-й ТС.
при обеспечении этим комплектом j-й ТС. . Величина xij, принимая неотрицательные целые значения, указывает на то, сколько ПМ типа i входит в комплект СПО, удовлетворяющий ТС вида j. Понятно, что для переменных xij должны выполняться ограничения bkj(x1j,…,xmj)³bkj, jÎX, k=1,…,K.
. Величина xij, принимая неотрицательные целые значения, указывает на то, сколько ПМ типа i входит в комплект СПО, удовлетворяющий ТС вида j. Понятно, что для переменных xij должны выполняться ограничения bkj(x1j,…,xmj)³bkj, jÎX, k=1,…,K. . (7)
. (7) . Величина xi равна 1, если ПМ i-го типа участвует в формировании комплекта СПО, и равна 0 в противном случае.
. Величина xi равна 1, если ПМ i-го типа участвует в формировании комплекта СПО, и равна 0 в противном случае.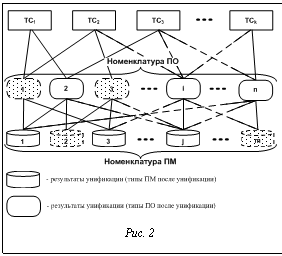 Формально задача выбора оптимальной системы СПО представляет собой двухуровневую задачу унификации и имеет вид
Формально задача выбора оптимальной системы СПО представляет собой двухуровневую задачу унификации и имеет вид ; (8)
; (8) ; (9)
; (9) ; (10)
; (10) . (11)
. (11) конкретного вида.
конкретного вида. удовлетворяет требованиям ТС j-го вида, если
удовлетворяет требованиям ТС j-го вида, если ; (12)
; (12) , (13)
, (13) – целые неотрицательные числа;
– целые неотрицательные числа;  – неотрицательная невозрастающая функция, равная 1 при q=1.
– неотрицательная невозрастающая функция, равная 1 при q=1. ; (15)
; (15) ; (16)
; (16) ; (17)
; (17) . (18)
. (18)