Software & Systems

Геометрическая концепция моделирования виртуальной среды на базе функционально заданных объектов [1] может быть описана как алгебраическая система:

(M, Ф, W),                                                             (1)

где M – множество геометрических объектов; Ф – множество геометрических операций; W – множество отношений на множество объектов.

Известны следующие функциональные способы задания примитивов. Поверхности свертки [2] – это интегральное представление неявно заданных поверхностей, известных в компьютерной графике как капельные модели [3], метасферы и мягкие объекты [4]. Функционально заданные геометрические объекты с применением функций возмущения изложены в [5].

В данной работе для визуализации использовался алгоритм многоуровневого отслеживания лучей, осуществляющий эффективный поиск точек поверхностей, участвующих в формировании изображения, а для определения столкновений объектов применялся этот же алгоритм с небольшой модификацией. Целью работы является  исследование возможности применения известных унарных, бинарных и более сложных геометрических операций для функционально заданных объектов на базе функций возмущения, а также утверждение, что с помощью модифицированного алгоритма столкновение объектов определяется за постоянное и меньшее время для различной сложности столкновений с полной гарантией обнаружения событий. Все манипуляции с функционально заданными объектами можно выполнять в интерактивном режиме, где определение столкновений объектов является одной из важнейших задач.

Геометрические объекты

Кратко определим функции возмущения [5]. Предложено описание геометрических объектов с помощью задания функций возмущения от базовых поверхностей (рис. 1). Свободная форма – это композиция базовой поверхности и возмущения:

F¢(x, y, z)= F(x, y, z)+ R(x, y, z),                   (2)

где R(x, y, z) – функция возмущения.

Задача конструирования объекта сводится к деформации базовой поверхности нужным образом, а не к аппроксимации ее примитивами. Предложенный способ описания объектов трехмерных сцен базовыми поверхностями и функциями возмущения имеет компактное описание, что позволяет уменьшить объем передаваемых данных от 10 до 1000 раз в зависимости от конкретных трехмерных сцен и моделей.

Геометрические операции

Множество геометрических операций Ф математически выражается следующим образом:

Фj: M1+M2+…+Mn®M.                                      (3)

Пусть объект G1 определен как f1(X)³0. Унарная операция (n=1) (3) объекта G1 означает операцию G2=Фj(G1) с определением

f2=y(f1(X))³0,                                                        (4)

где y – непрерывная вещественная функция одной переменной.

Рассмотрим следующие унарные операции.

Пусть исходный объект G1ÌEn описывается функцией f1(x1, x2, …, xi,…, xn)³0, а его проекция G2ÌEn-1 – функцией f1(x1, x2, …, xi,…, xn)³0. Объект G2 может быть определен как объединение сечений объекта G1 гиперплоскостью xi=Cj, где Cj+1=Cj+Dxi, j=1,N  и C1=ximin.

Пусть f1j=f1(x1, x2, …, xi-1, Cj, xi+1, …, xn) – функция для сечения. В итоге функция для проекции при Dxi®0 есть объединение всех функций f1j:

f2=f11Úf12Ú…Úf1jÚ…Úf1N.                                                   (5)

В реализации данной операции для всей сцены фиксировалась одна координата в зависимости от того, какую проекцию требовалось получить (рис. 2).

С помощью операции офсеттинга можно создавать увеличенную или уменьшенную копию исходного объекта, то есть делать положительный (расширение) или отрицательный (сжатие) офсеттинг соответственно (рис. 3).

Например, можно имитировать пульсацию тела. Пусть исходный объект задается функцией f(X)>0, тогда при применении такой операции полученное тело будет описываться функцией F=f(X)+C, где C<0 определяет отрицательный офсеттинг, а C>0 – положительный.

Пусть объекты G1 и G2 определены как f1(X)³0 и f2(X)³0. Бинарная операция (n=2) (3) объектов G1 и G2 означает операцию G3=Фj(G1, G2) с определением:

f3=y(f1(X), f1(X))³0  ,                                           (6)

где y – непрерывная вещественная функция двух переменных.

Геометрическая модель должна позволять конструировать объекты и их композиции неограниченной сложности (рис. 4 и 5). Достигается это в первую очередь применением булевых операций объединения и пересечения.

При метаморфозисе (морфинге) осуществляется плавный переход начального образа в конечный (рис. 6). Пусть имеются F1, F2 – значения функций возмущения первого и второго объектов, соответственно, тогда результирующая функция возмущения F вычисляется следующим образом:

F=bF1+(1-b)F2,                                                    (7)

где b – положительная непрерывная функция.

Рассмотрим сложные геометрические операции, а именно кручение и заметание движущимся твердым телом.

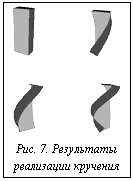
Кручение – деформация тела, являющаяся частным случаем биективного отображения (рис. 7), которое служит для определения деформаций исходных объектов. Для кручения исходного тела найдены и преобразованы координаты x, y, z.

Заметание движущимся твердым телом является одной из давних и трудных проблем в твердотельном моделировании. Рассмотрим заметание как проекцию движущегося тела из 4D(x,y,z,t)-пространства в 3D(x,y,z)-пространство. Вновь образованная фигура представляет собой объединение изображений заметающего тела при различных положениях (рис. 8).

Отношения

Одним из примеров отношений может служить определение столкновений между объектами. Бинарное отношение есть множество множества: M2=M´M. Оно может быть определено как

Sj: M´M®I.                                                         (8)

Пусть объекты G1 и G2 определены как f1(X)³0 и f2(X)³0. Бинарная операция пересечения объектов G1 и G2 определяется следующим образом:

                    (9)

Функция f3(X)=f1(X)&f2(X) может использоваться для вычисления Sc. Можно утверждать, что Sc=0, если f3(X)<0 для любой точки пространства En.

После вычисления пересечения (9), то есть применения булевой операции пересечения, поиск точки соприкосновения сталкивающихся объектов осуществляется с помощью алгоритма [5]. Применив особый тест на пересечение и бинарный поиск, можно за постоянное число шагов (определяется заданной точностью) отыскать точку столкновения объектов, если таковое происходит. В целях расчета времени обнаружения столкновений тестировались объекты, различавшиеся как по степени сложности (форме), так и по виду столкновения (в данном случае – по столкновению различными сторонами и частями объектов) (рис. 9).

Интерактивное создание форм

В последнее время компьютерная графика, связанная с интерактивным моделированием и редактированием трехмерных объектов, развивается быстрыми темпами. Для интерактивного редактирования полигональных моделей применяются известные коммерческие системы SoftImage, MAYA, 3DStudioMax и др. Существуют интерактивные системы на базе полиномов, неявных поверхностей, треугольных сеток, изображений, объемов, функционально заданных моделей.

Конструирование объекта в нашем случае напоминает лепку модели из пластилина с применением геометрических операций, представленных выше, и деформации (рис. 10, 11). Основное положительное отличие от известных интерактивных систем на базе функционально заданных моделей в том, что нет необходимости в полигонизации функциональной модели перед деформацией.

Программная модель алгоритма растрирования и структуры данных объектов реализована на языке высокого уровня С++. Этот язык хорошо подходит для реализации объектной модели описываемой системы, так как является объектно-ориентированным.

В данной работе исследованы различные геометрические операции для функционально заданных объектов на базе функций возмущения. Показана возможность реализации сложных геометрических операций (метаморфозис, проекции, офсеттинг, кручение, заметание) над объектами. В алгоритме определения столкновений функционально заданных объектов столкновение всегда определяется и не зависит от взаимного расположения сталкивающихся объектов и частей их поверхностей, то есть такой алгоритм гарантирует обнаружение события, что доказано экспериментально и теоретически, разброс времен при тестировании был не более 1 % от данного времени. В результате разработана инструментальная среда, в которой интерактивно можно создавать или редактировать функционально заданные объекты с применением функций возмущения без предварительной полигонизации. Реализованное программное обеспечение значительно упрощает создание функционально заданных моделей с применением функций возмущения.

Основные области применения результатов работы – это интерактивные графические системы визуализации функционально заданных объектов, CAD-системы 3D-моделирования, 3D-веб-визуа­лизация и т.д. В известных пакетах 3D-модели­рования стали применяться функциональные примитивы, например, метасферы (Meta Balls) в Strata Studio Pro. Важной прикладной задачей может стать применение предлагаемого функционального задания объектов для 3D-веб-визуализации, например, функционально базируемое расширение 3D (X3D), а также VRML (Virtual Reality Modeling Language). Функционально заданные объекты могут использоваться совместно со стандартными моделями X3D и VRML. Для этого необходимо разработать функциональные узлы на базе разработанных примитивов и методов их визуализации с целью уменьшения количества передаваемых данных.

Литература

1.   Pasko A.A., Adzhiev V.D., Sourin, A.I. et al. Function representation in geometric modeling: concepts, implementation and applications // The Visual Computer. 1995. № 11 (6), pp. 429–446.

2.   Bloomenthal J., Shoemake K. Convolution surfaces, SIGGRAPH’91, Computer Graphics, 1991. Vol. 25. № 4, pp. 251–256.

3.   Muraki S. Volumetric shape description of range data using «blobby model». Computer Graphics. July 1991. № 25 (4), pp. 227–235.

4.   Wyvill G., McPheeters C. and Wyvill B. Data structure for soft objects. The Visual Computer. 1986. № 2 (4), pp. 227–234.

5.   Алгоритм визуализации трехмерных данных, заданных поверхностями свободных форм / С.И. Вяткин [и др.] // Программные продукты и системы. 1999. № 3. С. 16–21.