Journal influence
Bookmark
Next issue
Analytical and numerical investigation of discrete structures evolution algorithms
The article was published in issue no. № 1, 2010Abstract:New algorithms for discrete structures evolution modeling are proposed and under analytical and numerical investigation in a new program EVOLDIST. Numerical tests show that this technique is appropriate for very complex non-linear natural phenomena simulation.
Аннотация:Предложены и аналитически исследованы некоторые алгоритмы моделирования эволюции дискретных структур, на их основе разработана программа EVOLDIST. Результаты численного моделирования позволяют сделать вывод о перспективности использования развитых подходов для исследования сложных нелинейных природных явлений
| Authors: (abelov@tversu.ru) - , (abelov@tversu.ru) - , Ph.D | |
| Keywords: non-linear phenomena, discrete structures, cellular automata |
|
| Page views: 9690 |
Print version Full issue in PDF (4.03Mb) Download the cover in PDF (1.25Мб) |
Известно, что при моделировании некоторых нелинейных явлений получить удовлетворительные результаты, хотя бы качественно адекватные наблюдаемым эффектам, часто удается только в рамках специфических подходов к численному моделированию, основанных на исследовании эволюции дискретных структур [1, 2]. Например, в рамках модели клеточного автомата удается получить решения типа спиральных волн для реакционно-диффузионных уравнений и другие нетривиальные нелинейные эффекты [2]. Поскольку вычислительная сложность сильно зависит от объема дискретной структуры (числа частиц), до настоящего времени в основном рассматривались системы с локальным характером взаимодействия (то есть в предположении о том, что изменение структуры в некоторой точке зависит только от соседей, находящихся в некоторой окрестности этой точки). Целью данной работы являются построение и изучение нелокальных алгоритмов моделирования эволюции дискретных структур и описание их реализации в программе EVOLDIST (Evolution of Discrete Structures). Математический формализм и постановка задач Дискретной структурой будем считать область
будем называть один из вариантов взаимного расположения шаров, где qi – сорт шара в i-м узле, i=1,…,N. Полной энергией системы будем считать
где
где Назовем единичной перестановкой обмен местами двух шаров разных сортов. Из конфигурации X единичной перестановкой получим конфигурацию где C – матрица единичной перестановки. Работой выхода, совершаемой при перемещении шара из узла i в узел j, будем считать
Для единичной перестановки вида (4) можно записать Процессом развития дискретной системы будем считать последовательное получение с помощью однократной перестановки шаров вида (4) новых конфигураций. При этом на k-м итерационном шаге выполняются условия минимизации:
где Пусть
где Изложенный в этом разделе математический формализм будем использовать при решении следующих основных задач. Задача 1. Эволюция дискретной структуры. На области D заданы начальная конфигурация X(0), энергия взаимодействия шаров Eij=E(qi, qj, rij) и работа выхода. Исследуем динамику развития дискретной структуры, получая новые конфигурации в соответствии с условиями (6)–(8). Задача 2. Минимум энергии системы. В области D задано количественное соотношение шаров различных сортов и энергии их взаимодействия. Необходимо найти конфигурацию с наименьшей энергией системы. Естественно, можно считать эту задачу частным случаем задачи 1, но имеющим самостоятельное значение и особенности алгоритмизации. Задача 3. Рост дискретной структуры. Как и в предыдущих задачах, рассмотрим систему взаимодействующих шаров с общей энергией (2). Единичным ростом R будем считать процесс получения конфигурации
Исследование эволюции дискретной системы в частных случаях При исследовании свойств алгоритмов для моделирования эволюции дискретных структур принципиальными являются вопросы быстроты сходимости и детерминированности алгоритма. Рассмотрим итерационный процесс получения цепочки конфигураций для задачи 1, считая Замечание: из этого утверждения видно, что график зависимости энергии получаемых конфигураций от номера итерационного шага является выпуклым вниз. Отметим, что в формулировке и доказательстве утверждения 1 не указан вид функции энергии взаимодействия между заряженными шарами. Для случая, когда E=E(qi, qj, rij) является монотонной, имеет место утверждение 2. Пусть двухкомпонентная система состоит из m шаров с зарядом q и N–m дырок – шаров с нулевым зарядом, плотно упакованных на прямой. Между заряженными шарами задана энергия взаимодействия Eij=E(qi, qj, rij), монотонно зависящая от rij. Тогда количество итерационных шагов алгоритма (6)–(8), требующееся для решения задачи 1, не превышает m. Доказанные утверждения позволяют оценить характер сходимости итерационных процессов, моделирующих развитие дискретных структур. Рассмотрим задачу 2 в отсутствие работы выхода для двухкомпонентной системы с монотонным притягивающим потенциалом взаимодействия. Заряды Рассмотрим задачу 1 для системы, состоящей из N=7 шаров, плотно упакованных на отрезке. Три шара несут единичный положительный заряд, остальные имеют нулевой заряд (дырки). Пусть заряды притягиваются и для определенности
В ряде случаев к условиям оптимальности перестановки, определяющим итерационный процесс эволюции системы, можно добавить дополнительные условия (соответствующие законам сохранения, топологической непрерывности структур и т.п.), что с математической точки зрения сводится к добавлению некоторых штрафных функций в условие оптимизации (6)–(8). Программа EVOLDIST для численного моделирования эволюции дискретных структур Для численного моделирования эволюции двухмерных двухкомпонентных дискретных структур разработана программа EVOLDIST. Эта программа имеет дружественный Windows интерфейс (рис. 2), позволяет интерактивно (время счета – порядка минут) исследовать поведение систем с количеством шаров порядка 10 тысяч.
Приведем некоторые типы парных взаимодействий, которые могут использоваться в программе EVOLDIST:
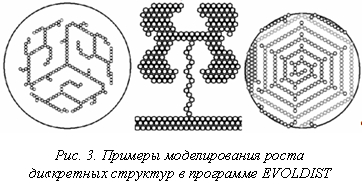
Естественно, для различных типов шаров (белый – белый, цветной – цветной, цветной – белый) могут задаваться различные взаимодействия (10). Некоторые, интересные, на взгляд авторов, результаты численного моделирования приведены на рисунке 3. В целом в программе EVOLDIST удается на качественном уровне получать нетривиальные картинки, характерные для нелинейных природных явлений [1, 2]. А ведь именно для исследования сложных нелинейных эффектов и предлагается использовать моделирование эволюции дискретных структур.
В настоящей работе сформулированы некоторые задачи моделирования эволюции дискретной структуры. Предложен удобный для их анализа и компьютерного моделирования математический формализм. Рассмотрены алгоритмы, учитывающие нелокальный характер взаимодействия шаров и основанные на минимизации целевой функции, зависящей от текущей конфигурации системы. Исследованы некоторые свойства и особенности предложенных алгоритмов (неоднозначность, характер сходимости, роль работы выхода, внешнего поля и др.). Численные эксперименты, проведенные в программе EVOLDIST, позволяют заключить, что компьютерное моделирование дискретных структур имеет некоторые преимущества по сравнению с численным решением уравнений математической физики на основе разностных схем [3] и применимо для исследования сложных нелинейных явлений и процессов в различных областях естествознания. На качественном уровне в программе EVOLDIST удается воспроизводить наблюдаемые в природе нетривиальные эффекты. Основной недостаток моделирования эволюции дискретных структур, связанный со значительной вычислительной сложностью, компенсируется постоянно растущими возможностями вычислительной техники. Следующим естественным шагом будет разработка программных продуктов для исследования эволюции трехмерных дискретных структур. Литература 1. Современные проблемы хаоса и нелинейности / К. Симо [и др.]. Ижевск: Ин-т компьютер. исследований, 2002. 2. Жаботинский А.М., Отмер Х., Филд Р. Колебания и бегущие волны в химических системах. М.: Мир, 1988. 3. Самарский А.А., Гулин А.В. Теория разностных схем. М.: Наука, 1989. |
| Permanent link: http://swsys.ru/index.php?id=2422&lang=en&page=article |
Print version Full issue in PDF (4.03Mb) Download the cover in PDF (1.25Мб) |
| The article was published in issue no. № 1, 2010 |
Perhaps, you might be interested in the following articles of similar topics:
 , n=1, 2, 3, покрытую равномерной кубической сеткой с шагом h, состоящей из N узлов, в каждом узле ri сетки находится шар радиусом h/2. Каждый шар характеризуется его принадлежностью к одному из S сортов. В дальнейшем конфигурацией
, n=1, 2, 3, покрытую равномерной кубической сеткой с шагом h, состоящей из N узлов, в каждом узле ri сетки находится шар радиусом h/2. Каждый шар характеризуется его принадлежностью к одному из S сортов. В дальнейшем конфигурацией (1)
(1) , (2)
, (2) – потенциальная энергия взаимодействия между шарами;
– потенциальная энергия взаимодействия между шарами;  – энергия шара в узле i, находящегося в поле шара узла j на расстоянии rij;
– энергия шара в узле i, находящегося в поле шара узла j на расстоянии rij;  – энергия системы во внешнем силовом поле. В дальнейшем будем рассматривать случай, когда энергия
– энергия системы во внешнем силовом поле. В дальнейшем будем рассматривать случай, когда энергия  , (3)
, (3) – симметричная матрица квадратичной формы, определяемая видом взаимодействия. При этом считаем, что
– симметричная матрица квадратичной формы, определяемая видом взаимодействия. При этом считаем, что  ,
,  . Заметим, если
. Заметим, если  , где
, где  – функция Хевисайда, получается локальное взаимодействие с характерным расстоянием d. При значениях d порядка шага сетки h получаются модели клеточных автоматов.
– функция Хевисайда, получается локальное взаимодействие с характерным расстоянием d. При значениях d порядка шага сетки h получаются модели клеточных автоматов. :
:  , (4)
, (4) . (5)
. (5) .
. , (6)
, (6) , (7)
, (7) , (8)
, (8) – матрица перестановок на k-м шаге.
– матрица перестановок на k-м шаге. – начальная конфигурация, тогда текущую конфигурацию
– начальная конфигурация, тогда текущую конфигурацию  можно представить в виде
можно представить в виде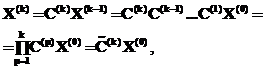 (9)
(9) – матрица k однократных перестановок вида (4).
– матрица k однократных перестановок вида (4).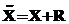 , где R – столбец с единственным ненулевым элементом в строке i. На k-м итерационном шаге получается конфигурация
, где R – столбец с единственным ненулевым элементом в строке i. На k-м итерационном шаге получается конфигурация .
. . Значения q=0 соответствуют невзаимодействующим шарам – «дыркам». Тогда в отсутствие работы выхода и внешнего силового поля будет выполняться утверждение 1. Для последовательно получаемых конфигураций в задаче 1 справедливо неравенство
. Значения q=0 соответствуют невзаимодействующим шарам – «дыркам». Тогда в отсутствие работы выхода и внешнего силового поля будет выполняться утверждение 1. Для последовательно получаемых конфигураций в задаче 1 справедливо неравенство  .
. плотно упакованы на отрезке [a, b] в узлах равномерной сетки xn=a+hn, n=0,…,N–1. Пусть m – число шаров с зарядом q и для определенности m=N/2. Тогда для задачи 2 сложность полного перебора при больших N будет порядка
плотно упакованы на отрезке [a, b] в узлах равномерной сетки xn=a+hn, n=0,…,N–1. Пусть m – число шаров с зарядом q и для определенности m=N/2. Тогда для задачи 2 сложность полного перебора при больших N будет порядка  . В соответствии с утверждением 2 сложность алгоритма (6)–(8) будет O(N3). Это делает возможным уже в настоящее время проводить интерактивное моделирование развития дискретных структур с числом ячеек
. В соответствии с утверждением 2 сложность алгоритма (6)–(8) будет O(N3). Это делает возможным уже в настоящее время проводить интерактивное моделирование развития дискретных структур с числом ячеек  на персональном компьютере.
на персональном компьютере. . Начальную конфигурацию определим как
. Начальную конфигурацию определим как  .
.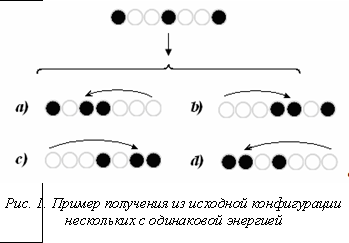 На рисунке 1 (a–d) показаны конфигурации с одинаковой энергией, которые могут быть получены из X(0) однократной перестановкой. Это иллюстрирует неоднозначность эволюции дискретных структур на основе алгоритма (6)–(8) при отсутствии работы выхода. Очевидно, что при включении в рассмотрение работы выхода Aij=arij неоднозначность уменьшается – остаются только варианты a) и b), так как в случаях c) и d) шары перемещаются на большее расстояние. Поэтому мы можем заключить, что учет работы выхода снимает неопределенность процесса эволюции дискретной системы с точностью до центрально-симметричных конфигураций a) и b). После разветвления на следующем шаге алгоритма неопределенности уже нет, но все последующие (и конечные) конфигурации, порождаемые, соответственно, ветвями a) и b), будут центрально-симметричными. Если, кроме работы выхода, добавить внешнее силовое поле, например
На рисунке 1 (a–d) показаны конфигурации с одинаковой энергией, которые могут быть получены из X(0) однократной перестановкой. Это иллюстрирует неоднозначность эволюции дискретных структур на основе алгоритма (6)–(8) при отсутствии работы выхода. Очевидно, что при включении в рассмотрение работы выхода Aij=arij неоднозначность уменьшается – остаются только варианты a) и b), так как в случаях c) и d) шары перемещаются на большее расстояние. Поэтому мы можем заключить, что учет работы выхода снимает неопределенность процесса эволюции дискретной системы с точностью до центрально-симметричных конфигураций a) и b). После разветвления на следующем шаге алгоритма неопределенности уже нет, но все последующие (и конечные) конфигурации, порождаемые, соответственно, ветвями a) и b), будут центрально-симметричными. Если, кроме работы выхода, добавить внешнее силовое поле, например  , направленное вдоль отрезка расположения шаров, то очевидно, неопределенность снимается полностью – шары соберутся вместе у одного края отрезка.
, направленное вдоль отрезка расположения шаров, то очевидно, неопределенность снимается полностью – шары соберутся вместе у одного края отрезка.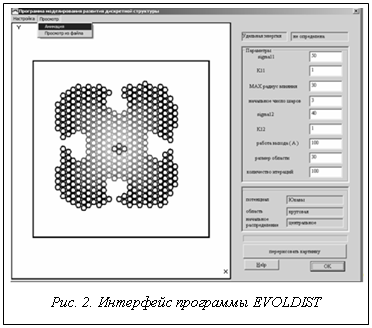 Пользователь задает тип области (прямоугольная, круговая), тип упаковки (квадратная, гексагональная), начальное распределение, типы потенциалов взаимодействия и параметры работы выхода. Для ускорения вычислений (при быстро убывающих с расстоянием взаимодействиях) можно задавать параметр эффективного радиуса влияния. Результат моделирования (все шаги итерационного процесса эволюции структуры) записывается в текстовый файл, поэтому пользователь может уже без вычислений просмотреть все шаги алгоритма в виде анимации и проанализировать изменение текущих параметров системы (таких, как полная энергия, энергия перехода, работа выхода, среднее число соседей, фрактальная размерность и т.п.). Программа позволяет моделировать и диффузионные процессы, и рост дискретной структуры.
Пользователь задает тип области (прямоугольная, круговая), тип упаковки (квадратная, гексагональная), начальное распределение, типы потенциалов взаимодействия и параметры работы выхода. Для ускорения вычислений (при быстро убывающих с расстоянием взаимодействиях) можно задавать параметр эффективного радиуса влияния. Результат моделирования (все шаги итерационного процесса эволюции структуры) записывается в текстовый файл, поэтому пользователь может уже без вычислений просмотреть все шаги алгоритма в виде анимации и проанализировать изменение текущих параметров системы (таких, как полная энергия, энергия перехода, работа выхода, среднее число соседей, фрактальная размерность и т.п.). Программа позволяет моделировать и диффузионные процессы, и рост дискретной структуры.
 (10)
(10)
 .
.