Задачи составления расписания носят самый общий характер. Они возникают там, где существует возможность выбора той или иной очередности выполнения требований: при составлении расписания движения поездов и самолетов, распределении работ на производстве, планировании деятельности образовательных и административных учреждений.
 Когда процесс обслуживания каждого требования включает только одну стадию и может быть осуществлен одним ресурсом, расписание представляет собой простую последовательность операций, которые необходимо выполнить ресурсам – сотрудникам, устройствам, оборудованию. Такие расписания называют одностадийными.
Когда процесс обслуживания каждого требования включает только одну стадию и может быть осуществлен одним ресурсом, расписание представляет собой простую последовательность операций, которые необходимо выполнить ресурсам – сотрудникам, устройствам, оборудованию. Такие расписания называют одностадийными.
Если же каждое выполняемое требование задействует несколько ресурсов в заранее заданной последовательности, операция должна содержать не только ссылку на исходное требование, но и порядковый номер данной операции в списке операций требования. Такие расписания обычно называют многостадийными. Наиболее простой пример подобного расписания – план работ по обработке одной детали на нескольких станках [1].
Однако очень часто на практике структура расписаний имеет более сложный характер, когда итоговый план представляет собой составной объект, связывающий множество участников и операций, которые они выполняют на разных стадиях бизнес-процесса с учетом логической последовательности места и времени. То есть расписание – это не просто набор независимых требований, размещенных на рабочих графиках однотипных ресурсов, а совокупность задач, одновременно использующих несколько различных ресурсов.
В этом случае построение допустимого расписания, учитывающего множество связей, отражающих порядок следования и согласования задач, зачастую является довольно сложной задачей. Еще более она усложняется, когда требуется найти оптимальный вариант расписания.
Рассмотрим несколько примеров предметных областей, демонстрирующих специфику внутренних связей расписания. Наглядным примером является расписание школьных занятий, когда каждая операция (урок) должна хранить данные о нескольких участниках: преподаватель, аудитория, класс.
Более сложное расписание работы водителей и машин в компаниях, сдающих автомобили в аренду (rent-a-car), поскольку в каждый момент водитель как ресурс, выполняя передвижения по доставке/забору машин и подвозу пассажиров, решает несколько задач [2]. Расписание в такой предметной области – это сложное взаимодействие различных ресурсов с большим числом причинно-следственных связей, описывающих необходимость существования тех или иных подзадач, операций, участков расписания. Пример расписания работы нескольких водителей и машин показан на рисунке 1. Особенностью такого плана является сильная связанность всех ресурсов, когда расписание одного участника тесно переплетается с другими и почти не может быть изменено без серьезного перестроения всего плана.
Для разработки эффективных систем планирования очень важно выявить характеристики и природу внутренних связей вышеприведенных расписаний, а также предложить модель, которая позволила бы описать процесс обслуживания каждого требования.
Проанализировав несколько подобных типов расписаний, можно выделить наиболее общие аспекты, нашедшие отражение в расписании каждой из рассмотренных предметных областей:
· в качестве исходных данных на планирование поступает последовательность требований;
· процесс обслуживания каждого требования включает использование нескольких ресурсов;
· последовательность обслуживания требования каждым ресурсом не определена заранее, а зависит от внутреннего состояния и расписания ресурсов;
· в один момент несколько ресурсов могут выполнять операции, относящиеся к обслуживанию одного требования;
· возможно многократное использование ресурса в процессе облуживания одного требования.
Такой анализ позволяет предположить, что процесс обслуживания каждого требования – это поэтапное разбиение одной задачи на несколько подчиненных подзадач и последовательное выполнение их различными ресурсами. Так, например, чтобы выполнить работу по доставке автомобиля из точки A в точку B, необходимо создать подчиненные задачи подвоза водителя в точку A перед работой и возврата его на станцию с точки B после выполнения работы. То есть в общем случае перед выполнением или после выполнения работы требуется осуществить мероприятия по подготовке ресурса к ней. Классическим примером может являться процесс переналадки станка перед операцией или после ее выполнения.
Таким образом, необходимо вести учет расписания дополнительного ресурса, который будет осуществлять подготовку основного ресурса. То есть фактически необходимо создавать новую задачу, подчиненную главной, и выполнять ее планирование, размещая операцию подготовки в расписании дополнительного ресурса.
Но если дополнительную задачу по подготовке основного ресурса рассматривать как идентичную главной, можно утверждать, что в процессе размещения ее операций также возможно создание новой дополнительной задачи. В итоге получается, что каждая задача, размещаясь на ресурсах, может создавать для себя подчиненные задачи независимо от занимаемого в этой иерархии места, то есть расписания можно описывать с помощью древовидной структуры, позволяющей отражать причинно-следственные связи процесса обслуживания требований.
 Рассмотрим модель такого типа расписаний. Итак, имеются конечное множество требований N={n1, n2, …, nk} и конечное множество ресурсов R={r1, r2,…, rn}. Будем считать, что процесс обслуживания каждого требования состоит только из одной стадии и может осуществляться только одним ресурсом, то есть допускается только непрерывная обработка требования. При этом каждому требованию iÎN сопоставляется множество ресурсов RiÍR, такое, что требование i должно быть обслужено любым из ресурсов LÍRi, но не более чем одним одновременно.
Рассмотрим модель такого типа расписаний. Итак, имеются конечное множество требований N={n1, n2, …, nk} и конечное множество ресурсов R={r1, r2,…, rn}. Будем считать, что процесс обслуживания каждого требования состоит только из одной стадии и может осуществляться только одним ресурсом, то есть допускается только непрерывная обработка требования. При этом каждому требованию iÎN сопоставляется множество ресурсов RiÍR, такое, что требование i должно быть обслужено любым из ресурсов LÍRi, но не более чем одним одновременно.
Для описания иерархии работ исполнения требований введем понятие задачи как единицы основной и дополнительной работы для подготовки ресурса к выполнению требования. Каждая задача будет соответствовать одному из типов задач из множества T={t1, t2,…, tn}. При этом каждому типу задачи iÎT сопоставляется множество ресурсов RiÍR, такое, что только ресурсом из множества Ri может быть выполнена данная задача.
Таким образом, для каждого требования iÎN задается своя, специфическая для этого требования последовательность типов задач Bi=(Ti1,Ti2,…, , состоящая из bi количества элементов, где
, состоящая из bi количества элементов, где  , которая означает, что задача типа Tij должна быть выполнена перед выполнением
, которая означает, что задача типа Tij должна быть выполнена перед выполнением
требования i основным ресурсом. Таким же образом необходимо задать последовательность типов задач  , где
, где  , которые должны быть выполнены после выполнения требования i основным ресурсом. Кроме того, такие же последовательности можно задавать не только для требований, но и для каждого типа задачи из множества T. Tо есть можно определять
, которые должны быть выполнены после выполнения требования i основным ресурсом. Кроме того, такие же последовательности можно задавать не только для требований, но и для каждого типа задачи из множества T. Tо есть можно определять  и
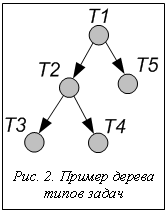
и  для iÎT. Это будет означать, что перед выполнением и после выполнения задачи типа i ресурсом необходимо выполнить дополнительные задачи типов, входящих в последовательности Bi и Ai. На рисунке 2 показан пример получаемого дерева типов задач, если
для iÎT. Это будет означать, что перед выполнением и после выполнения задачи типа i ресурсом необходимо выполнить дополнительные задачи типов, входящих в последовательности Bi и Ai. На рисунке 2 показан пример получаемого дерева типов задач, если 
 .
.
Итак, была предложена новая модель расписаний, учитывающая сложную структуру связей между элементами расписания и позволяющая описывать широкий класс таких прикладных задач, в которых древовидная организация процесса обслуживания и функционирования имеет большое значение.
На основе предложенной модели разработан алгоритм, а также программно реализована система автоматизированного построения расписаний, которая была внедрена в качестве основной системы оперативного планирования в британском отделении международной компании по сдаче автомобилей в аренду.
Литература
1. Танаев В.С., Сотсков Ю.Н., Струсевич В.А. Теория расписаний. Многостадийные системы. М.: Наука, 1989.
2. Andreev S., Rzevski G., Shviekin P., Skobelev P., Yankov Igor. A Multi-Agent Scheduler for Rent-a-Car Companies // 4th International Conference on Industrial Applications of Holonic and Multi-Agent Systems, Linz, Austria, 2009.
3. Handbook of Scheduling: Algorithms, Models and Performance Analysis. Edited by J. Y-T. Leung // Chapman & Hall / CRC Computer and Information Science Series, 2004.

 Рассмотрим модель такого типа расписаний. Итак, имеются конечное множество требований N={n1, n2, …, nk} и конечное множество ресурсов R={r1, r2,…, rn}. Будем считать, что процесс обслуживания каждого требования состоит только из одной стадии и может осуществляться только одним ресурсом, то есть допускается только непрерывная обработка требования. При этом каждому требованию iÎN сопоставляется множество ресурсов RiÍR, такое, что требование i должно быть обслужено любым из ресурсов LÍRi, но не более чем одним одновременно.
Рассмотрим модель такого типа расписаний. Итак, имеются конечное множество требований N={n1, n2, …, nk} и конечное множество ресурсов R={r1, r2,…, rn}. Будем считать, что процесс обслуживания каждого требования состоит только из одной стадии и может осуществляться только одним ресурсом, то есть допускается только непрерывная обработка требования. При этом каждому требованию iÎN сопоставляется множество ресурсов RiÍR, такое, что требование i должно быть обслужено любым из ресурсов LÍRi, но не более чем одним одновременно. , состоящая из bi количества элементов, где
, состоящая из bi количества элементов, где  , которая означает, что задача типа Tij должна быть выполнена перед выполнением
, которая означает, что задача типа Tij должна быть выполнена перед выполнением , где
, где  , которые должны быть выполнены после выполнения требования i основным ресурсом. Кроме того, такие же последовательности можно задавать не только для требований, но и для каждого типа задачи из множества T. Tо есть можно определять
, которые должны быть выполнены после выполнения требования i основным ресурсом. Кроме того, такие же последовательности можно задавать не только для требований, но и для каждого типа задачи из множества T. Tо есть можно определять  и
и 
 .
.