Для динамического моделирования процесса ликвидации кризисной ситуации (КС) выбрана нотация, базирующаяся на языке сетей Петри. Выбор обусловлен сочетанием мощного математического аппарата сетей Петри с наглядностью представления, возможностями моделирования причинно-следственных связей между событиями параллельных и конфликтных ситуаций, с оценкой временных и случайных характеристик протекающих процессов.
В основе моделирования КС на сетях Петри лежит декомпозиция процесса развития ситуации на множество отдельных взаимодействующих между собой процессов, сущность которых состоит в преобразовании параметров (характеристик) текущей ситуации во времени.
Для оперативного реагирования на событие ситуационный центр работает в трех режимах.
Нормальный режим работы. Центр отслеживает те или иные процессы в конкретной сфере управления, фиксирует показатели, зна- чения, всплески активности на той или иной территории, в отрасли, среди определенных групп населения.
Плановый режим. Развитие ситуации планируется, и группа экспертов формирует доклад с вариантами решения, с возможностью получения необходимой информации из хранилищ ситуационного центра, обратившись к БД и БЗ, с разработкой системы моделирования.
Кризисный режим работы. Происходит событие, сведения о котором отсутствуют в БД и БЗ, и необходимо собрать оперативную информацию о нем, смоделировать ситуацию, предложить решение, активным образом участвовать в предотвращении разрастания КС.
Одной из основных задач ситуационного центра является сокращение времени, необходимого для оценки и понимания КС с целью выработки и принятия соответствующего решения [1].
Модели процессов управления и принятия решений в условиях КС должны удовлетворять следующим требованиям:
- обеспечивать возможность моделирования взаимосвязанных процессов различной природы, протекающих при КС;
- обеспечивать выделение моментов принятия решений по ликвидации КС и описание состава решений (управление ликвидацией КС включает совокупность решений по выполнению частных задач перевода аварийной ситуации в нормальную);
- отражать временной аспект моделируемых процессов (учет динамических характеристик процессов, протекающих при развитии и ликвидации чрезвычайной ситуации, во многом определяет эффективность принимаемых решений);
- формализовать знания экспертов о ликвидации КС;
- обеспечивать адекватное отображение информационного аспекта с помощью фиксации структуры информации, используемой при ликвидации КС;
- обеспечивать количественную оценку планов и принимаемых решений;
- обеспечивать учет пространственного аспекта (модели должны учитывать распределенный характер протекающих при ликвидации КС процессов) [2].
Для учета этих требований необходимо создать соответствующие системные модели и методы, взаимоувязывающие разнотипные модели и обеспечивающие моделирование различных аспектов исследуемой предметной области.
В данной работе была актуализирована группа методов, применяемых для динамического оценивания состояния, а также использованы недетерминированные модели сетей Петри, потому что недетерминизм модели позволяет априорно оценить возможные КС и альтернативные пути их устранения.
Ожидаемые события были смоделированы переходами. Последовательная реализация событий в системе отображается в сети в виде последовательного срабатывания ее переходов. Выполнение какого-либо условия в системе связано с появлением метки в соответствующей этому условию позиции. Действующие в сетях Петри соглашения о правилах выполнения переходов выражают логические взаимосвязи между условиями и событиями в моделируемой системе. Недетерминизм развития кризисной ситуации вводится в модель с помощью функции вероятности возникновения событий P1(t) и функции вероятности развития процесса P2(t).
 Каждая функция вероятности должна иметь плотность вероятности, релевантную как возникновению того или иного события, так и собственно развитию процесса. А развитие того или иного процесса может описываться таким законом ве- роятности, который соответствует развитию природных или социальных явлений, явившихся причиной КС или сопутствующих ей, а в случае техногенной катастрофы закон релевантен протеканию физико-химических или иных реакций в природной среде.
Каждая функция вероятности должна иметь плотность вероятности, релевантную как возникновению того или иного события, так и собственно развитию процесса. А развитие того или иного процесса может описываться таким законом ве- роятности, который соответствует развитию природных или социальных явлений, явившихся причиной КС или сопутствующих ей, а в случае техногенной катастрофы закон релевантен протеканию физико-химических или иных реакций в природной среде.
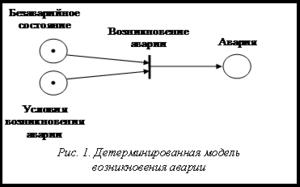
Возникновение аварии зачастую описывается моделью, представленной на рисунке 1.
Данная модель по сути является детерминированной, так как исходное количество и расположение меток в сети Петри определены априорно.
Предлагается ввести недетерминизм двух типов.
Первый тип недетерминизма описывает случайную функцию P1(t) передачи метки из одной позиции в другую посредством добавления в модель третьей, по сути фиктивной позиции с меткой, удовлетворяющей закону распределения вероятности появления тех или иных условий возникновения КС.
Пусть плотность распределения вероятности возникновения условий законом Пуассона равна 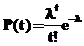 , где t – формальный параметр, который может иметь физическую интерпретацию, например, время или температуру и т.п.; l – интенсивность потока. Тогда процесс возникновения КС описывается зависимостью не только от условий возникновения, имеющих детерминированный характер, но и от вероятности их возникновения, которая в меняющейся обстановке может иметь различные распределения. Это вызвано тем, что условия возникновения аварийной ситуации на технической системе не всегда ведут к предсказуемой аварии, а являются лишь неотъемлемой причиной среди прочих факторов. Полное формальное описание условий возникновения КС на таком сложном объекте, как, например, ГЭС, невозможно и во многом зависит от комбинации случайных факторов. Поэтому в данной статье предлагается ввести недетерминизм в описание условий возникновения КС.
, где t – формальный параметр, который может иметь физическую интерпретацию, например, время или температуру и т.п.; l – интенсивность потока. Тогда процесс возникновения КС описывается зависимостью не только от условий возникновения, имеющих детерминированный характер, но и от вероятности их возникновения, которая в меняющейся обстановке может иметь различные распределения. Это вызвано тем, что условия возникновения аварийной ситуации на технической системе не всегда ведут к предсказуемой аварии, а являются лишь неотъемлемой причиной среди прочих факторов. Полное формальное описание условий возникновения КС на таком сложном объекте, как, например, ГЭС, невозможно и во многом зависит от комбинации случайных факторов. Поэтому в данной статье предлагается ввести недетерминизм в описание условий возникновения КС.
Второй тип недетерминизма описывает случайную функцию передачи меток из одной вершины в n других вершин посредством добавления в модель дополнительной вершины и генерирующей n-1 меток при получении метки на своем входе. Это обусловлено тем, что развитие КС и возможные варианты ее устранения также зависят от множества случайных факторов, комбинацию которых невозможно предусмотреть заранее.
Степень неопределенности случайных факторов вводится нормальным ненормированным центральным распределением 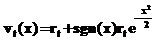 , где x – равномерно распределенная на отрезке [a,b] случайная величина,
, где x – равномерно распределенная на отрезке [a,b] случайная величина, 
Значение q определяет диапазон изменения абсолютного значения комбинации случайных факторов r в момент t. Предлагаемая модель позволяет моделировать недетерминированные природные и техногенные процессы, к которым можно отнести не только скорость развития КС, но и время до начала ее развития.
Динамическая модель развития КС позволяет получить прогноз развития обстановки в виде изменения вектора параметров метки с некоторым временным шагом. Полученный прогноз характеризует наихудший сценарий развития КС, который подразумевает полное бездействие системы управления КС (рис. 2).
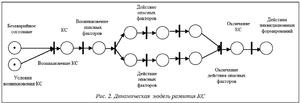
Модифицированную сеть Петри, моделирующую развитие и ликвидацию КС, можно пред- ставить набором N=(C, E, F, P, m0), где С – множество позиций, соответствующих состояниям; E – непустое множество переходов/процессов; F: C´E´C®N – отображение сети Петри в сеть Петри; P – вероятность отображения F; m0 – начальная разметка сети, заключающаяся в наличии маркеров с заданными параметрами в определенных позициях – состояниях.
Сформулируем определение процесса Ei. Пусть известны такие состояния Ci и Cj, что Ci, Cj: F(Ci, Ei, Cj, Pi).
Множество процессов E состоит из трех подмножеств: E={Ed, Er, Eи}, где Ed – действия ликвидационных формирований; Er – физико-хи- мические процессы развития КС; Eи – условные процессы взаимодействия процессов Еr и Еd при смене состояний.
Множество состояний С представлено подмножеством состояний развития аварии Сa и подмножеством Сd, моделирующим действия по ликвидации КС: C=CaÈCd, Ca={C2, C3, C4, …, C9}, Cd={C1, C10}.
Модель представляет собой динамическую БД позиций и переходов сети, выполнение которых зависит от случайной функции. В модели использованы распределение Пуассона P1(t) для вероятности возникновения КС (переход E1) и равномерная функция вероятности P2(t) возникновения сопутствующих опасных факторов (переход E2).
На каждом шаге работы модели выводятся текущие характеристики:
- шаг моделирования (определенный период времени),
- выполненный переход,
- передача меток от входных сигналов к выходным.
Кроме этого, в случае невозможности перехода по причине внесенного в модель недетерминизма осуществляется пустой переход, моделирующий течение времени, когда никакие события не происходят.
В качестве примера рассматривалась нестандартная ситуация: вследствие аварии на высоковольтной линии была прекращена подача электроэнергии с энергосистемы в регион. В связи с этим отключено энергопотребление на всей территории региона. При возобновлении подачи электроэнергии происходит сбой, вследствие чего потребители остались неподключенными. Ситуация осложнилась возгоранием силового трансформатора и одновременно с этим при попытке повторного подключения электроэнергии на котельную произошел гидроудар, что вызвало порыв на тепловой сети. Отключено теплоснабжение части потребителей, прекращена работа водозабора.
Имитационное моделирование данной ситуации производилось в среде CPN Tools, была построена цветная сеть Петри (рис. 3).
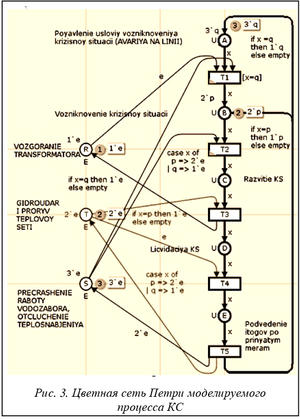
Использование построенной цветной сети Петри позволило оценить потенциальную опасность каждого фактора риска (условия возникновения КС) и собрать статистический материал для последующего анализа и выработки мер по противодействию (предупреждению) возникновению КС в результате действия того или иного фактора либо их группы.
Заметим, что построенную модель в виде сети Петри можно рассматривать и как вспомогательный инструмент анализа, когда для построения системы используются общепринятые методы проектирования и впоследствии построенная система (принятия решений в КС) моделируется сетью Петри, а модель подвергается анализу. В таком случае трудности и ошибки, выявляемые в ходе анализа, указывают на изъяны в проекте и необходимость его модификации с последующим итерационным моделированием; этот цикл повторяется до тех пор, пока проводимый анализ не приведет к успеху.
Однако разрабатываемая модель в основном используется для анализа уже существующих, действующих в настоящее время систем. В таком случае в ходе проектирования требуется постоянное преобразование системы в модель в виде сети Петри; методы анализа применяются только для создания адекватного проекта сети Петри. В обоих случаях необходимы методы анализа сетей Петри для определения свойств модели, и основная задача будет заключаться в преобразовании представления сети Петри в реальную рабочую систему.
Задачами ситуационного центра в режиме КС являются оперативное реагирование на ситуацию и выработка действий по уменьшению или полной ликвидации последствий КС. В данной работе предложена методика построения динамической модели в виде сети Петри развития КС, а алгоритм отбора комбинаций ликвидационных мероприятий позволяет:
- оптимизировать сценарий ликвидации КС во взаимодействии с ЛПР;
- эффективно и обоснованно выбирать план ликвидации на основе полученных прогнозных оценок и потерь;
- управлять оптимальным размещением сил и средств для ликвидации поражающих факторов КС;
- моделировать причинно-следственные связи между возникающими поражающими факторами и др.
При этом в нормальном режиме работы ситуационным центром должны осуществляться следующие мероприятия:
- сбор информации для прогнозирования возможного развития КС и ее последствий;
- построение модели на основании собранной информации;
- проведение нескольких циклов моделирования;
- разработка на основании проведенного моделирования различных превентивных планов, позволяющих эффективно реагировать на возникающие проблемы.
Кроме того, следует накапливать сведения о ресурсах, необходимых для ликвидации проблем.
Литература
1. Филиппович А.Ю. Ситуационные центры: определения, структура и классификация // PCWeek/RE. 2003. № 26 (392). С. 21–22.
2. Ямалов И.У. Моделирование процессов управления и принятия решений в условиях чрезвычайных ситуаций. М.: Лаборатория Базовых Знаний, 2007. 288 с.
3. Симанков В.С. Автоматизация системных исследований: монография. Краснодар, КубГТУ, 2002. 376 с.

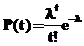 , где t – формальный параметр, который может иметь физическую интерпретацию, например, время или температуру и т.п.; l – интенсивность потока. Тогда процесс возникновения КС описывается зависимостью не только от условий возникновения, имеющих детерминированный характер, но и от вероятности их возникновения, которая в меняющейся обстановке может иметь различные распределения. Это вызвано тем, что условия возникновения аварийной ситуации на технической системе не всегда ведут к предсказуемой аварии, а являются лишь неотъемлемой причиной среди прочих факторов. Полное формальное описание условий возникновения КС на таком сложном объекте, как, например, ГЭС, невозможно и во многом зависит от комбинации случайных факторов. Поэтому в данной статье предлагается ввести недетерминизм в описание условий возникновения КС.
, где t – формальный параметр, который может иметь физическую интерпретацию, например, время или температуру и т.п.; l – интенсивность потока. Тогда процесс возникновения КС описывается зависимостью не только от условий возникновения, имеющих детерминированный характер, но и от вероятности их возникновения, которая в меняющейся обстановке может иметь различные распределения. Это вызвано тем, что условия возникновения аварийной ситуации на технической системе не всегда ведут к предсказуемой аварии, а являются лишь неотъемлемой причиной среди прочих факторов. Полное формальное описание условий возникновения КС на таком сложном объекте, как, например, ГЭС, невозможно и во многом зависит от комбинации случайных факторов. Поэтому в данной статье предлагается ввести недетерминизм в описание условий возникновения КС.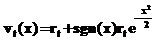 , где x – равномерно распределенная на отрезке [a,b] случайная величина,
, где x – равномерно распределенная на отрезке [a,b] случайная величина, 


