Journal influence
Bookmark
Next issue
Management of educational process
The article was published in issue no. № 1, 2010Abstract:In clause the model of management of educational process at the resource centre is considered.
Аннотация:В статье рассмотрена модель управления образовательным процессом в ресурсном центре.
| Authors: (wkz@rambler.ru) - , Ph.D, (wkz@rambler.ru) - , Ph.D, (wkz@rambler.ru) - , Ph.D | |
| Keywords: making a model (scheme), educatioal process, control management |
|
| Page views: 15847 |
Print version Full issue in PDF (4.03Mb) Download the cover in PDF (1.25Мб) |
Концепция образовательной реформы основными задачами ресурсного центра предполагает формирование, организацию и мониторинг образовательного процесса начального профессионального образования на территории округа; проведение и поддержку государственной политики на территории округа в области законодательства, перспектив развития, стратегии обучения и т.п.; мониторинг и поддержку в соответствии с государственной политикой лицеев, осуществляющих обучение на территории округа, а также методическое обеспечение образовательного процесса, сертификацию, лицензирование и др. [1]. Рассмотрим модели управления образовательным процессом. Пусть состояние учебного процесса в образовательном центре характеризуется функцией Х(x1, x2,…,xn), где x1, x2,…xn – частные показатели учебного процесса. Его состояние в некоторый i-й момент можно обозначить X(ti). Управление учебным процессом заключается в выработке неких управляющих директив u(ti®ti+1), которые переводят состояние системы X(ti), соответствующее моменту ti, в состояние X(ti+1) для момента ti+1. При этом на систему воздействуют внешние помехи Образовательный центр является иерархической организацией, его структура состоит из уровней управления, на каждом из которых, кроме высшего, может быть несколько органов или отделов. Тогда для некоторого l-го органа управления на уровне k можно формально записать выражение вектора Ф – выбора модели стратегии управления, обеспечивающей оптимальное функционирование системы в виде
где Результатом такой оптимизации будет некоторый заданный план
где Внешняя среда в виде воздействия
где F – формальный оператор, переводящий реальное состояние системы Тогда формальное описание процесса управления можно представить в виде
где Предложены алгоритмы F1 и F2, обеспечивающие оптимальный учебный процесс. Алгоритм F1 заключается в организации мониторинга за состоянием учебного процесса. Для этого вначале разрабатываются тестовые задания, представляющие собой срезовые контрольные работы, контрольные работы соответствующих разделов, самостоятельные работы, опросы в ходе лабораторных и практических работ и т.п. Цель разработки – выделение основных элементов необходимых знаний учебного материала и основных навыков практической работы. Для этого определяются требования к задачам, которые войдут в банк тестовых заданий, и оптимальные варианты, обеспечивающие достоверный контроль большого количества студентов по различным разделам. Оценка знаний каждого ученика осуществляется по 10-балльной шкале, формируемой вместе с заданием. Затем составляется план проведения тестовых заданий. Обработка результатов проводится методами математической статистики. В интервалы 0=t1, …, ts=T определяются математическое ожидание [2], Mx[X(tk)]≈x(tk)= =
За оценку нормированной корреляционной функции принимается
Таким образом, получаются временные ряды:
которые описывают зависимость соответствующих числовых характеристик от времени tÎ[0, T]. Тогда математическое ожидание Mx(t) показывает общее направление изменения процесса усвоения знаний в целом. Дисперсия Dx(t) и среднее квадратичное отклонение σx(t) характеризуют течение учебного процесса по изменению разброса значений результатов относительно среднего Mx(t) во времени. По значениям rx(t) и rxy(t) можно проследить, как изменяется во времени сила связи между сечениями для одной случайной функции X(t) и любых двух X(t) и Y(t). Заметим, что в последнем случае интерес могут представлять функции rx(t) и rxy(t) для всевозможных пар значений k и l (k≠l). На основе полученных значений проводится статистический анализ влияния на показатели учебного процесса различных факторов: содержание обучения, распределение времени по обучаемым дисциплинам, установление последовательности и взаимосвязи их изучения, определение сложности и объема изучаемой информации, времени использования технического оборудования, мотивация обучения по отношению к степени востребованности на рынке труда, роли педагогов в изучении данных дисциплин. Такой анализ проводится стандартными методами регрессионного и дисперсионного анализа. Полученные результаты позволяют сформировать управляющие воздействия на учебный процесс F2, который базируется на мнении экспертов. Основными мероприятиями являются: - оптимизация выбора профессии с точки зрения ее востребованности на рынке труда, постоянное повышение квалификации учеников, отслеживание их трудоустройства и организация переподготовки, сотрудничество с центром занятости и другими организациями; - модернизация материально-технической базы, поставка нового оборудования, инструментов, станков, компьютеров, ПО, использование кредита Международного банка реконструкции и развития в рамках пилотных проектов; - изменение содержания обучения, распределения времени по обучаемым дисциплинам, последовательности и взаимосвязи их изучения; - изменение графика заседания предметно-цикловой комиссии, где принимаются коррективы учебных планов, организации и распорядка ведения учебного процесса; - повышение квалификации педагогов и их постоянное сотрудничество и взаимодействие, в частности, мастера производственного обучения и преподавателя спецтехнологии, организация совместных зачетов по разделам; - распространение передового опыта учителей, изучение новых педагогических технологий и их использование на уроках, в частности, бинарные уроки, создание презентаций, видеофильмов по предметной области (сварке, устройству автомобилей), развивающее и проблемное обучение, коллективные способы обучения и т.д. Важную роль играют премирование лучших педагогов по итогам мониторинга, а также изменение содержания и плана проведения мониторинговых мероприятий. Литература 1. Анциферова В.И., Сербулов Ю.С., Зольников В.К. Методы управления образовательным процессом // Моделирова- ние систем и информационные технологии: межвуз. сб. науч. тр. Воронеж: Изд-во «Научная книга», 2006. Вып. 3. Ч. 2. 2. Математическая статистика: учеб. для вузов / В.Б. Горяинов [и др.]. М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. 424 с. |
| Permanent link: http://swsys.ru/index.php?id=2457&lang=en&page=article |
Print version Full issue in PDF (4.03Mb) Download the cover in PDF (1.25Мб) |
| The article was published in issue no. № 1, 2010 |
Perhaps, you might be interested in the following articles of similar topics:
- Основные задачи автоматизации управления образовательным процессом
- Унифицированное описание функционирования информационных радиоэлектронных систем для оценки программного обеспечения учебно-тренировочных средств
- Система управления бизнес-процессами и административными регламентами
- Проблемы управления конфигурациями в процессе разработки программного обеспечения встроенных систем
- Имитационно-тренажерные и обучающие распределенные системы
Back to the list of articles
 с момента ti до момента ti+1.
с момента ti до момента ti+1.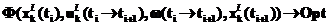 , (1)
, (1) – состояние системы для органа
– состояние системы для органа  в момент ti;
в момент ti;  – состояние системы для органа
– состояние системы для органа  – управляющие директивы органа
– управляющие директивы органа  функционирования органа управления, который может быть представлен в виде следующей функции:
функционирования органа управления, который может быть представлен в виде следующей функции: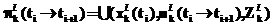 , (2)
, (2) – знак операции, означающей объединение, согласование и агрегирование планов органа
– знак операции, означающей объединение, согласование и агрегирование планов органа  – множество показателей (в том числе нормативные требования вышестоящего органа управления) плана.
– множество показателей (в том числе нормативные требования вышестоящего органа управления) плана.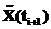 . Чтобы привести его в требуемое состояние, необходимы корректирующие воздействия:
. Чтобы привести его в требуемое состояние, необходимы корректирующие воздействия: , (3)
, (3) в требуемое Х. Степень отклонения определяется мониторингом. Его результаты позволяют выделить так называемый шум, то есть отличия реальной системы от идеальной.
в требуемое Х. Степень отклонения определяется мониторингом. Его результаты позволяют выделить так называемый шум, то есть отличия реальной системы от идеальной.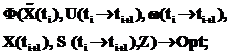 (4)
(4) m=1,…,M;
m=1,…,M; ,
, – частные показатели учебного процесса (данные мониторинга); F1 – оператор (алгоритм), формирующий представление об объекте управления с помощью средств мониторинга;
– частные показатели учебного процесса (данные мониторинга); F1 – оператор (алгоритм), формирующий представление об объекте управления с помощью средств мониторинга;  – суммирующие воздействия, представляющие собой выбор стратегии F2 по всем управляющим директивам
– суммирующие воздействия, представляющие собой выбор стратегии F2 по всем управляющим директивам 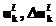 всех органов
всех органов  – стимулирование управляющих директив для достижения требуемого состояния системы; Opt – оператор реализации векторной процедуры оптимизации по критерию качества Z, который характеризует степень подготовки ученика.
– стимулирование управляющих директив для достижения требуемого состояния системы; Opt – оператор реализации векторной процедуры оптимизации по критерию качества Z, который характеризует степень подготовки ученика. /n, и дисперсия, Dx[X(tk)]≈
/n, и дисперсия, Dx[X(tk)]≈ (tk)= =
(tk)= =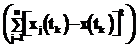 /(n-1) (где
/(n-1) (где 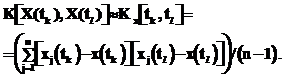
 .
.  ,
, ,
, ,
,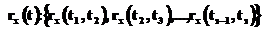 ,
, ,
,