Software & Systems

Одной из классических схем организации вычислительных систем была кольцевая модель, имеющая свои преимущества и недостатки. На современном этапе чаще используются модели типа «звезда» или «дерево». В работах [1–3] исследуются планетарные вычислительные системы со структурой, близкой к древовидной и одновременно включающей подсистемы типа «звезда». Для таких систем в указанных работах рассматривается влияние процессов разрушения и починки. В работах [4–5] исследуются системы с полным графом, корпоративные вычислительные системы (КВС), которые идеально подходят для изучения эффектов, возникающих при росте системы, то есть не только процессов разрушения и восстановления существующих элементов, но и добавления новых. Еще одним подходом к изучению процессов роста может быть фиксация структуры графа системы (необязательно полносвязного) и рассмотрение набора одинаковых систем, граф которых имеет указанную структуру. Для данной работы в качестве графа выбрано кольцо, а системы, соответственно, названы кольцевыми вычислительными системами (КлВС). На первый взгляд может показаться, что отказоустойчивость такой системы крайне мала: разрушение одного элемента превращает граф в линейную структуру, что, например, в случае компьютерных сетей, основанных на протоколах работы с использованием маркера, могло привести к выходу из строя всей системы. Однако, если использование каких-либо передаваемых по кольцу маркеров не рассматривается, а граф задачи, которую требуется решить, совпадает с графом КлВС, образ задачи в некоторых случаях может быть найден и на разрушенной КлВС. Простейший пример – КлВС с элементами лишь двух типов. Для этой системы достаточно, чтобы работоспособными оставались хотя бы два соседних элемента разных типов: на такой разрушенной КлВС можно выполнить любую двухцветную задачу. Возможность выполнения задачи на разрушенной КлВС и ее зависимость от параметров графа системы также стали предметом рассмотрения в настоящей работе.

Результаты машинного эксперимента достаточно четко очерчивают границы двух классов КлВС по признаку возможности выполнения задачи на разрушенной системе. Несколько неожиданными оказались результаты машинного эксперимента с кольцами разной длины, но если принять указанное выше разделение систем на классы, результаты этих испытаний выглядят естественно.

  Моделирование функционирования КлВС Понятие кольцевой системы и задачи. Модель КлВС рассматривается в виде направленного графа с помеченными вершинами, где метки (цвета) вершин соответствуют типам узлов, а дуги – двунаправленным каналам передачи данных. Граф КлВС имеет кольцевую структуру, то есть элементы графа могут быть упорядочены и каждый следующий элемент связан с предыдущим и следующим элементом, и только с ними. Первый элемент также связан с последним.

Модель задачи основана на модели КлВС, более того, граф задачи в точности совпадает с графом системы. В случае выхода из строя компонентов КлВС оставшаяся работоспособной часть системы называется разрушенной КлВС (РКлВС). В работе рассматривается только разрушение узлов системы, каналы передачи данных считаются абсолютно надежными. Разрушение каналов данных можно имитировать путем введения дополнительных вершин.

Поиск образа задачи на графе системы. Для возможности выполнения задачи на РКлВС необходимо ассоциировать каждую вершину графа задачи с вершиной графа РКлВС того же типа так, чтобы при этом в полученном образе задачи на графе РКлВС существовали все дуги, соответствующие дугам на графе модели задачи. В данной работе рассматривается случай, когда несколько однотипных вершин графа модели задачи могут ассоциироваться с одной и той же вершиной РКлВС того же типа. При этом предполагается, что локальные пересылки данных с одного узла ВС на самого себя всегда возможны.

Под разложимостью графа модели задачи на граф РКлВС понимается возможность ассоциировать каждую вершину модели задачи с некоторой вершиной РКлВС того же типа. При этом, если между двумя вершинами графа модели задачи есть дуга, между образами вершин модели задачи на графе РКлВС также должна быть дуга либо образы этих вершин должны совпадать. В случае, когда модели задачи разложима на РКлВС, полученный набор образов вершин модели задачи на графе РКлВС называется образом задачи. Если граф модели задачи совпадает с графом исходной КлВС, для неразрушенной КлВС в качестве образа задачи может быть выбран сам граф КлВС. При этом граф модели задачи по определению имеет кольцевую структуру, однако образ модели задачи на КлВС может не быть кольцевым.

Генерация графа системы. Для КлВС был задан процесс генерации вероятностного типа с двумя основными характеристиками: количеством вершин S и количеством цветов C.

При генерации КлВС каждая вершина получает цвет как реализацию равновероятного испытания Бернулли на множестве цветов: 1, …, С.

Разрушение и восстановление. Для моделирования процессов разрушения и восстановления системы задаются два параметра: Pd – вероятность разрушения одного узла и Pf – вероятность починки одного узла.

Один цикл разрушения графа РКлВС проводится следующим образом: для каждого узла РКлВС проходит испытание Бернулли с вероятностью успеха Pd. В случае успеха узел и все инцендентные ему дуги исключаются из графа РКлВС. Восстановление осуществляется аналогично: для всех узлов исходной КлВС, не содержащихся в графе РКлВС, производится испытание Бернулли с вероятностью успеха Pf. В случае успеха узел и все инцендентные ему дуги, идущие к другим узлам РКлВС, добавляются в граф РКлВС. После одного цикла разрушения и восстановления при моделировании делается попытка разложения модели задачи на полученный граф РКлВС, поэтому порядок следования операций разрушения и восстановления важен [3]. В данной работе используется последовательность DR (destruct-repair), то есть каждый этап жизни системы состоит из разрушения, последующего восстановления и попытки разложения модели задачи на РКлВС.

Набор КлВС

Рост. Набор КлВС – это множество, состоящее из E одинаковых КлВС.

Разрушенный набор – набор КлВС, в котором все или некоторые КлВС подвергались разрушению и восстановлению.

Отказ разрушенного набора – ситуация, при которой ни на одной (Р)КлВС из набора не может быть найден образ модели задачи.

Процесс роста разрушенного набора задается добавлением в набор одной или нескольких копий исходной, неразрушенной КлВС. В работе исследовались наборы систем с логарифмическим законом роста и количество систем (в том числе полностью разрушенных) в наборе на i-й итерации эксперимента E(i)=E0+ëE1log2(i+2)û, где скобки ë û – операция округления вниз до ближайшего целого числа. В программных обозначениях E0=E0, E1=E1. Логарифмический рост выбран для экспериментальной проверки теоретического вывода о достаточности такой скорости роста для получения положительной вероятности не ограниченной по времени безотказной работы. Для этой цели естественно выбрать исходную систему с низкой отказоустойчивостью, например КлВС.

Алгоритм моделирования и сбора статистики. Помимо указанных параметров S, C, Pd, Pf, E0 и E1, для моделирования функционирования наборов КлВС задаются дополнительно Ni – общее количество итераций разрушения–восста­новления–роста–проверки в одном эксперименте, а также Ne – количество повторений эксперимента с целью сбора статистики.

Для проведения однократного эксперимента применялся следующий алгоритм.

1.   Согласно параметрам S и C генерируется исходный граф КлВС.

2.   Исходный граф копируется и сохраняется в качестве модели задачи.

3.   Создается набор, состоящий из E(0)=E0+E1 копий исходного графа.

4.   Запускается первая итерация эксперимента.

На каждой i-й итерации эксперимента

1)  производится разрушение всех РКлВС из набора с использованием вероятности разруше- ния Pd;

2)  производится починка всех РКлВС из набора с использованием вероятности починки Pf;

3)  происходит рост набора: к набору добавляются k копий исходной КлВС, причем k выбирается так, чтобы всего в наборе было E(i) систем, считая полностью разрушенные;

4)  производится попытка разложения модели задачи на все (Р)КлВС из набора. Если ни на одной системе из набора образ задачи не был найден, эксперимент завершается, наработка набора T в данном эксперименте устанавливается рав- ной i-1.

Если достигнута итерация с номером Ni и отказ на ней получен не был, T устанавливается равным Ni и эксперимент прекращается, считаясь успешным. Если T

Для сбора статистики указанный эксперимент проводится Ne раз, причем вычисляются средняя наработка – среднее арифметическое всех значений T, а также величина F – количество успешных экспериментов. Величина F является предметом исследования при варьировании разнообразных параметров алгоритма.

Результаты численного эксперимента

Варьирование количества типов элементов. В данной серии экспериментов варьировался параметр С – количество типов элементов. Результаты представлены в виде поверхностей, полученных по значениям функции F(C, Pf), где C – количество типов элементов; Pf – вероятность починки; F – количество успешных экспериментов.

Эксперимент 1. Постоянные параметры эксперимента: начальное количество копий КлВС E0=100; скорость роста набора E1=0 (рост отсутствует); вероятность разрушения Pd=0,1. Максимальное количество итераций эксперимента Ni=100; количество повторений каждого эксперимента Ne=1000; длина кольца S=10. Переменные параметры: число цветов C меняется от 2 до 100 с шагом 2; вероятность восстановления Pf меняется от 0,1 до 0,4 с шагом 0,01.

Описание и анализ результата. При C=2 все системы сохранили работоспособность. Это связано с сохранением достаточно большого числа исправных двухцветных пар.

При Pf£0,21 для всех C³10 частота выживания обнуляется, но с ростом вероятности починки примерно до 0,27 для всех значений С выходит на 100 %. Это связано с большим начальным числом КлВС. В этом эксперименте (табл. 1) зависимость от числа цветов очень слабая для C³10.

Таблица 1

Фрагмент таблицы значений F(C, Pf) по результатам эксперимента 1

Эксперимент 2. Число вершин S=100; параметр Pf варьируется от 0,7 до 0,83 с шагом 0,01; остальные параметры такие же, как в эксперименте 1.

Описание и анализ результата. С увеличением длины кольца при числе цветов C³3 вероятность выживания системы резко падает в сравнении с экспериментом 1. Это связано с ростом числа цветных подграфов исходной системы, которые надо воспроизвести на разрушенной системе. При С=2 сохраняется полная выживаемость при всех вероятностях ремонта. Для других значений С при Pf£0,76 частота выживания обнуляется. В интервале C³3 для 0,77£Pf£0,8 происходит быстрый рост частоты выживания почти до 100 % (табл. 2). Зависимость от числа цветов при C³3 слабая.

Таблица 2

Фрагмент таблицы значений F(C, Pf) по результатам эксперимента 2

В обоих экспериментах пределы изменения Pf подбирались вручную для включения в результаты эксперимента области перехода функции F(C, Pf) с нулевых значений к значениям Ni.

Варьирование длины кольца. После анализа результатов экспериментов 1 и 2 был проведен эксперимент 3, в котором варьировались параметры S и C. Постоянные параметры: начальное количество копий КлВС E0=20; скорость роста набора E1=0 (не растет); вероятность разрушения Pd=0,3; вероятность починки Pf=0,6; максимальное количество итераций эксперимента Ni=100; количество повторений каждого эксперимента Ne=1000. Переменные параметры: длина кольца S изменяется от 2 до 30, шаг 1; количество типов элементов С изменяется от 2 до 50, шаг 1.

Описание и анализ результата. При S>10 и C>4 наработка на отказ F была близка к 0. Для С=2 наработка остается 100 при всех S. При малых 2

Таблица 3

Фрагмент таблицы значений F(S, C) по результатам эксперимента 3

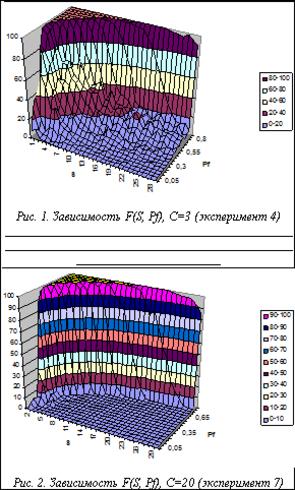В экспериментах 4–7 варьировались параметры S и Pf при различных С в разных экспериментах. Постоянные параметры: начальное количество копий КлВС E0=20; скорость роста набора E1=0 (не растет); вероятность разрушения Pd=0,3; максимальное количество итераций эксперимента Ni=100; количество повторений каждого эксперимента Ne=1000. Переменные параметры: длина кольца S варьируется от 2 до 30, шаг 1; вероятность починки Pf варьируется от 0,05 до 0,9, шаг 0,05; количество С типов элементов принимало значения 3, 5, 10, 20 соответственно в экспериментах 4, 5, 6, 7.

Описание и анализ результата. Эти эксперименты показали, что при всех значениях С наработка F с ростом S монотонно уменьшается. При S выше 16 наступает относительная стабилизация наработки на низком уровне. При этом для высоких значений Pf³0,65 начинается быстрый рост наработки до значений, близких к 100. С ростом C происходит некое уменьшение наработки, которое почти стабилизируется при C³5. На рисунках 1 и 2 показаны крайние по значениям C поверхности зависимости F(S, Pf). Неровности поверхности связаны со статистическими флуктуациями средних значений. Графики для 5£C£10 близки к графику при C=20.

Эти результаты подтверждают уменьшение зависимости количества успешных экспериментов от S и от C по мере роста их значений.

Рост наборов систем. Основной и исходной целью разработки ПО для моделирования наборов РКлВС было изучение изменения значений F в зависимости от основного параметра роста – E1. Эксперименты 8 и 9 были посвящены этому вопросу.

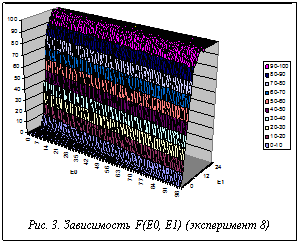
Эксперимент 8. Постоянные параметры: вероятность разрушения Pd=0,3; максимальное количество итераций эксперимента Ni=100; количество повторений каждого эксперимента Ne=1000; длина кольца S=100; вероятность починки Pf=0,5; количество типов элементов C=3. Переменные параметры: начальное количество копий КлВС E0 варьируется от 0 до 100, шаг 1; скорость роста набора E1 варьируется от 0 до 30, шаг 1.

Описание и анализ результата. Как и ожидалось, по обеим переменным наработка F растет. В соответствии с теорией при достаточно большом параметре логарифмического роста E1 наработка выходит на высокие значения, близкие к 100 при всех значениях начального количества копий E0. Крутизна роста F по Е1 близка при всех значениях Е0, но начинается он при различных значениях Е1. Для Е0=1 рост начинается с Е1=5. При Е0=90 рост начинается сразу при Е1=1. Линия начала роста в плоскости в указанных пределах близка к прямой. При дальнейшем росте Е0 линия роста совпадает с осью Е0=0. Крутизна роста характеризуется изменением F от 0 до 100 при DE1»12. График представлен на рисунке 3.

Эксперимент 9. Это дополнительный эксперимент, в котором варьировались параметры C и E1. Его параметры в основном повторяют параметры эксперимента 8.

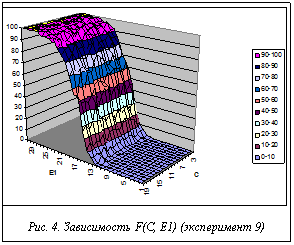
Постоянные параметры: вероятность разрушения Pd=0,3; максимальное количество итераций эксперимента Ni=100; количество повторений каждого эксперимента Ne=1000; длина кольца S=100; вероятность починки Pf=0,5. =3; начальное количество копий КлВС E0=0. Переменные параметры: скорость роста набора E1 варьируется от 0 до 30, шаг 1; количество типов элементов C варьируется от 3 до 20, шаг 1.

Описание и анализ результата. Результаты эксперимента 9 показывают практически полную независимость значений F(C, E1) от C, в том числе и при значении C, равном 3, которое использовалось в эксперименте 8. При E1<12 наработка практически нулевая. Потом начинается плавный рост наработки до значения около 100 при Е1=27. Линейный участок роста при 15£E1£21. При росте Е1 после значения 21 происходит плавный выход на константу 100 (рис. 4).

Общий анализ полученных данных. Классы систем

Результаты экспериментов 1–3 четко показывают резкое увеличение количества успешных экспериментов при снижении С до значения 2. При C=1 эксперимент выродился бы в поиск хотя бы одного исправного узла в любой из РКлВС. При C, равном 2, достаточно найти хотя бы два разнотипных связанных исправных элемента, так как любая двухцветная задача может быть разложена на граф РКлВС, состоящий из двух указанных элементов.

Одним из интересных результатов работы стало то, что при увеличении C всего лишь до 3 эффект непропорционально высокого количества успешных экспериментов практически пропадает. Этот факт можно объяснить так: если КлВС разрушена, любая оставшаяся исправной подсистема не является кольцом, то есть не замкнута. Подсистемы, не имеющие какого-либо из цветов, присутствующих в задаче, не позволяют выполнить ее. В случае трехцветных графов возможно существование трех неизоморфных связных подсистем длины 3, имеющих все три цвета: 1-2-3, 1-3-2 и 2-1-3 (здесь цифрами обозначены тип элемента, его «цвет», а дефисами – связи между элементами). В каждой из таких подсистем отсутствует связь между элементами каких-либо двух типов: 1 и 3 для первой, 1 и 2 для второй, 2 и 3 для третьей. Таким образом, любую задачу, требующую наличия соответствующей связи, невозможно разложить на соответствующую подсистему РКлВС. Не спасает положение и возможность удлинения рассматриваемых подсистем: добавление недостающей связи (путем добавления соответствующей вершины графа) в произвольном месте подсистемы не приведет к автоматической разложимости задачи на эту подсистему, так как граф модели задачи задает необходимый ему порядок следования элементов различного типа. Автоматическая разложимость любой трехцветной задачи достигалась бы на полносвязном графе, состоящем из трех разнотипных вершин, но этот граф является кольцом, а РКлВС нет.

Вообще автоматическая разложимость произвольной (даже не кольцевой) задачи естественно достигается на полносвязном графе системы, имеющем вершины всех возможных цветов. Подсистема РКлВС, состоящая из вершин всех возможных цветов, теряет свойство полносвязности при увеличении количества цветов до 3, и количество успешных экспериментов при этом резко падает.

Таким образом, можно рассматривать два класса систем и процессов разрушения: системы, граф которых обладает свойством после разрушения оставлять подсистемы, в которых есть полносвязный подграф из всех присутствующих в подсистеме типов элементов, и все прочие. Увеличение C от 2 к 3 переводит КлВС из одного класса в другой. Дальнейшее (при C>3) увеличение количества цветов слабо влияет на параметры системы, что, например, ярко демонстрируют результаты экспериментов 1, 2 и 9.

При рассмотрении параметра S следует отметить, что с его уменьшением естественным образом уменьшается и C, так как количество реально используемых типов элементов всегда не более S. При увеличении S быстро накапливаются требования к наличию разнообразных связей между элементами и быстро падает количество успешных экспериментов.

При достаточно больших значениях С и S эксперимент практически сводится к поиску полностью работоспособной КлВС, граф которой по определению совпадает с графом задачи. Возможность работы модели задачи на РКлВС в таких условиях практически отсутствует.

Варьирование параметров E0 и E1 приводит к результатам с четкой структурой. С увеличением E0 количество успешных экспериментов растет линейно. Разрушение может компенсироваться и размером начального набора, и ростом количества КлВС во время эксперимента. В целом количество успешных экспериментов монотонно растет по количеству КлВС в наборе. При малом Е0 основную роль берет на себя скорость роста набора систем, причем эксперименты 8 и 9 подтверждают достаточность логарифмического роста.

Литература

1. Коганов А.В., Сазонов А.Н. Анализ отказоустойчивости вычислительной среды планетарного типа // Математика. Компьютер. Образование: сб. науч. тр. Междунар. науч. конф.; под ред. Г.Ю. Ризниченко. М.–Ижевск: НИЦ «Регулярная и хаотическая динамика». 2006. Т. 2. Вып. 13. С. 235–248.

2. Коганов А.В., Сазонов А.Н. Анализ критических точек отказоустойчивости вычислительной среды планетарного типа. // Там же. 2007. Т. 2. Вып. 14. С. 179–186.

3. Коганов А.В., Сазонов А.Н. Анализ критических точек отказоустойчивости вычислительной среды планетарного типа // Программные продукты и системы. 2007. № 3. С. 27–31.

4. Коганов А.В., Сазонов А.Н. Анализ отказоустойчивости вычислительной среды корпоративного типа // Математика. Компьютер. Образование: сб. науч. тр. Междунар. науч. конф.; под ред. Г.Ю. Ризниченко. М.–Ижевск: НИЦ «Регулярная и хаотическая динамика». 2006. Т. 2. Вып. 13. С. 228–234.

5. Коганов А.В., Сазонов А.Н. Корпоративные вычислительные сети с разрушением и восстановлением. Фазовый переход в растущих сетях // Там же. 2007. Т. 2. Вып. 14. С. 48–59.