Journal influence
Bookmark
Next issue
Process model of the aggregated requirements forming to the complex information systems
The article was published in issue no. № 2, 2010Abstract:The article considers the information systems constructing for the science, designing, engineering organizations, academies which is directed to work with the documentation common for all branches of science and technology. The authors analyze ways of the un-ification, compression, and calculation problem solving with the help of the fuzzy set theory.
Аннотация:Рассматривается создание информационных систем для научно-исследовательских, проектных, конструкторских организаций, вузов, ориентированных на поддержку работы с документацией, характерной для всех областей науки и техники. Анализируются способы решения проблем объединения, сжатия и вычленения существенных требований на основании теории нечетких множеств.
| Authors: (tva@npo-rit.ru) - , Ph.D, (tva@npo-rit.ru) - , (tva@npo-rit.ru) - | |
| Keywords: complex information systems, aggregated requirements |
|
| Page views: 13013 |
Print version Full issue in PDF (4.97Mb) Download the cover in PDF (1.38Мб) |
Создание информационных систем для научно-исследовательских, проектных, конструкторских организаций, вузов, научно-производственных и производственных объединений, ориентированных на поддержку работы с документацией, характерной для всех областей науки и техники, является крайне актуальной проблемой. Это многоэтапный процесс, имеющий, как правило, не одну стадию. Реализацию его начинают с разработки требований к создаваемой системе любого типа. Наиболее популярными моделями процессов, используемыми в области информационных технологий, являются две – каскадная и спиральная. В каскадной модели в качестве точек оценки и перехода от одной фазы к другой используются вехи. Все задачи одной фазы должны быть завершены до начала следующей. Каскадная модель оптимально работает, когда на начальном этапе проекта можно четко определить неизменный набор требований к разрабатываемому решению. Фиксация переходов от одной фазы к другой облегчает распределение ответственности, отчетность и следование календарному графику про- екта [1]. Спиральная модель учитывает необхо- димость постоянного пересмотра, уточнения и оценки проектных требований, что очень эффективно при быстрой разработке небольших проектов. Такой подход стимулирует активное взаимодействие проектной группы и заказчика, поскольку заказчик оценивает ход и результаты работы на протяжении всего проекта. Недостатком спиральной модели является отсутствие четких вех, что может привести к хаотизации процесса разработки [2]. Дальнейшая тенденция развития этих моделей связана с опытом компании Microsoft, которая выпустила пакет руководств по эффективному проектированию, разработке, внедрению и сопровождению решений, построенных на основе своих технологий. Эти знания представлены в виде двух связанных и хорошо дополняющих друг друга областей знаний – Microsoft Solutions Framework (MSF) и Microsoft Operations Framework (MOF). Модель процессов MSF объединяет в себе лучшие принципы каскадной и спиральной моделей.
Для принятия решения целесообразно и необходимо привлекать людей, имеющих опыт успешной реализации аналогичных систем. На любом уровне работа должна вестись с единственной целью – удовлетворение условного заказчика с более высокого уровня, для чего необходимо привлекать к работе поставщиков, находящихся уровнем ниже [2]. Анализ тенденций, существующих в методиках выдвижения требований, позволил предложить усовершенствованный подход к решению данной задачи. Сущность его заключается в том, что, основываясь на принципе поэтапной разработки программного продукта, наиболее целесообразным является выявление так называемых вех (ключевых точек) на каждом этапе проектирования, их сопровождение на всем этапе разработки программного продукта, а также возможное выявление новых. Схематично предложенная интегрированная модель представлена на рисунке 2, где ромбы соответствуют вехам, стрелки – фазам, а каждый виток спирали – уровню разработки программного продукта.
Основным источником требований к информационной системе со стороны заказчика являются бизнес-требования и требования пользователей. Другим важным источником информации, помимо требований, являются артефакты, описывающие предметную область. Это могут быть документы с описанием бизнес-процессов предприятия, выполненные консалтинговым агентством, либо внутренние документы предприятия (должностные инструкции, распоряжения, своды бизнес-правил). Одной из немногих методологий, в которой специально выделяется рабочий поток делового моделирования, является Rational Unified Process. Кроме того, при выявлении требований используются так называемые «лучшие практики», широко применяемые в бизнес-консалтинге и при внедрении корпоративных информационных систем. В России единственным документом, закрепляющим необходимость формирования требований к системам, является ГОСТ 34.601-90, в соответствии с которым после этапа формирования (выявления) требований к системе выполняется этап разработки концепции системы, заключающийся в изучении объекта, проведении НИР, разработке вариантов концепции автоматизированной системы, оформлении отчета о выполненной работе. Чтобы требования стали хорошей базой для разработки системы, необходимо определить проверочные критерии для каждого из них, впоследствии используемые для подтверждения того, что разработанная система удовлетворяет требованиям заказчика. Помимо проверочных критериев, определяют и условия, в которых будет производиться проверка соответствия системы критериям приемки. Основная проблема при формировании требований – это объединение, сжатие и вычленение существенных требований. Сжатие требований позволит снизить проблемы перегрузки. Объединение, сжатие и вычленение существенных требований – проблема агрегирования требований к документации – в общем случае родственна теории нечетких множеств, и подходы к решению должны базироваться на ее положениях и методах. Для разработки методов агрегирования в соответствии с подходами теории нечетких множеств необходимо определить модель информационной системы документирования как формальной системы, выбрать схему обработки данных при агрегировании и определить существенные признаки, особенности требований и критерии агрегирования требований к документации. Важную роль при выполнении агрегирования имеющихся требований играют априорные требования, к которым относят множество уже существующих требований к документации и системам документирования [3]. При этом задачи, возникающие при построении системы, их формальная постановка и методы решения отображаются на домен креативного формально-технологического класса. Под формальной технологией Т понимается упорядоченная пара <А, F>, состоящая из двух конечных множеств: множества А некоторых исходных элементов (в нашем случае – множества априорных требований) материальной или нематериальной природы, называемых обычно элементами базы: A={a1, a2, a3,…, an}, и множества операций F={F1, F2, F3,…, Fm} над конечным числом элементов базы и (или) объектов (в нашем случае – операции агрегирования требований к системе), полученных в каких-либо предыдущих операциях технологии Т, причем ни одна из операций в F не может быть выражена через другие [4]. Формулировка задачи отражает содержательную часть методики, связанной с построением ИТ. В данном случае задача заключается в определении исчерпывающего перечня требований, характеризующих систему с полнотой, необходимой и достаточной для ее реализации в рамках, определенных заказчиком, и границах возможностей разработчика, то есть необходимо найти своего рода компромисс между затратами, которые готов понести заказчик, и объемом качественного продукта, который в сложившейся ситуации (объем финансирования, время на разработку продукта, уровень развития науки и т.п.) может реализовать разработчик. Примирить заказчика и разработчика призваны заранее обговоренные требования, а также последующее их согласование по мере работы над проектом. Определенная совокупность требований должна быть сформирована безотносительно к каким-либо ограничениям, связанным с получением априорной информации, необходимой для исходного описания элементов системы. Наоборот, первоначально следует определить все требования, хотя бы в малейшей мере необходимые для разработки системы, и лишь затем проводить их выборку – агрегирование. Группы требований формируются по функциональному назначению (для групп требований в литературе используют критерий модульности) на основе общности решаемых задач, составляющих группу. По косвенным признакам можно принять решение об их сходстве. Возможность отождествления интуитивного понятия сходства задач позволяет предположить, что классу схожих объектов (то есть группе) соответствует компактное множество точек, а разным образам соответствуют удаленные друг от друга компактные множества. Ввиду сложности и большого объема еди- ничных требований, предъявляемых к информационным системам документирования, задачу агрегирования приходится решать, не имея четкой классификации анализируемых объектов – единичных требований, а зная только пространство, в котором желательно провести классификацию. Одной из тенденций, сложившихся при обработке больших объемов информации, является разбиение множества обрабатываемых данных на классы толерантности по некоторому рефлексивному и симметричному отношению. Часто таким отношением служит отношение близости по некоторой метрике. Следующим шагом является выделение системы представителей для классов толерантности и формирование системы эталонных представителей. Реализация данного подхода приводит к необходимости решения комбинаторных задач, связанных с определением существования системы различных представителей для семейства множеств, и определения числа систем различных представителей, удовлетворяющих всевозможным ограничениям. Среди ограничений такого рода обычно используются ограничения на различимость представителей, которая может вводиться как принадлежность различным классам по некоторому отношению эквивалентности либо через значения весовой функции. Вследствие этого наиболее целесообразно использовать методы и принципы теории нечетких множеств. Теория нечетких множеств базируется на математическом аппарате теории множеств с допущением о том, что каждый элемент множества входит в него с некоторой вероятностью. Функция, задающая вероятность вхождения во множество всех ее элементов, называется характеристической функцией этого множества [5]. По мере развития знаний, представлений, предположений допускаются и строятся различные уровни моделей: ZI, ZII. При этом каждый уровень является базой для последующего. Рассматриваемая система характеризуется крайне высокой параметрической перегруженностью, что ведет к большой размерности вектора A=a(a1, …, an)ÎRn предполагаемых базовых параметров aj – единичных требований. Часто перечисление всех существующих требований невозможно и нерационально. В этих случаях отбирают наиболее значимые из них, а описание осществляют на уровне формальных моделей ZI, ZII. Цель агрегирования состоит в том, чтобы на основе модели предыдущего уровня точными или приближенными методами получить модель следующего уровня. Производя последовательное агрегирование множеств требований с первого уровня до самых высоких, можно получить совокупность групп требований к системе на различных уровнях разработки. Требования нижних уровней будут служить основой информационного обеспечения требований верхних уровней. Метод последовательного агрегирования дает возможность понять, какие допущения, предположения, упрощения положены в основу требований верхних уровней. Предположим, что на k-м уровне разработки системы сформировано первоначальное множество А¢ единичных требований р к системе документирования. В ходе агрегирования требований осуществляются операции примитивной декомпозиции и примитивного синтеза. Операцией примитивной декомпозиции называется операция Fd(p)®áy, añ, позволяющая отсоединить элемент aÎA¢ от необходимых требований p, где p – единичное требование к системе; а – требование, не удовлетворяющее условию; y – рациональное множество требований уровня. Необходимо проанализировать полезность выявленных требований. Каждое сформированное требование должно удовлетворять определенным условиям, соответствовать предъявляемым к требованиям свойствам. Мера соответствия является субъективной оценкой. В этом случае целесообразно использовать элемент аппарата нечетких множеств, а именно функцию принадлежности m: A¢®[0, 1]. Таким образом, из сформированного множества A¢ первоначальных требований необходимо выделить множество A, единичные требования которого будут соответствовать критериям, предъявляемым к требованиям. Используя функцию принадлежности m: A®[0, 1], которая представляет собой субъективную меру соответствия единичного требования формируемому множеству требований – множеству A, осуществляются операции декомпозиции. Для построения функции принадлежности наиболее целесообразно использовать метод экспертных оценок. После проверки каждого требования на соответствие установленным нормам и выборки наиболее правильных на k-м уровне определена первоначальная модель Zk. Необходимо произвести агрегирование данной модели, используя метод примитивного синтеза для формирования групп требований по принципу модульности (функциональности). Для удобства обозначим агрегированную модель идентификатором Z*k, а процесс агрегирования Z*k=Ag(Zk), где Ag – оператор или процедура агрегирования. В ходе агрегирования формируется М групп требований с номерами i=1,2,...,М. Каждому требованию рi группы i присвоим порядковый номер j, где j=1,...,n, при этом pij – единичное требование i-й группы; pin – максимальное число требований группы i. Группу требований, сформированную после агрегирования требований множества А, обозначим Ai, при этом Таким образом, На следующем этапе (k+1) разработки системы и формирования требований к ней в результате расширения и уточнения появляется новое множество требований B¢. Каждое сформированное требование группы В¢ также должно соответствовать предъявляемым к требованиям свойствам. Аналогично множеству А¢ требований на k-м уровне, используя функцию принадлежности для множества В¢, выявляют полезные требования, которые формируют множество требований В на (k+1)-м уровне. Аналогично множеству А необходимо произвести агрегирование требований В также по типам групп i, где i=1, 2, ..., N (N – максимальное число групп типа i множества В, причем N может быть любым: N£M, N³M). Каждому единичному требованию q множества B того же типа i присвоим порядковый номер j, где j=1, ..., n; при этом qij – единичное требование i-й группы; qin – максимальное число единичных требований множества В типа i. В ходе агрегирования имеющейся модели на (k+1)-м уровне Zk+1 по принципу модульности (функциональности) появляется агрегированная модель Z*k+1=Ag(Zk+1), которая обладает На (k+1)-м уровне вновь сформированное множество В представляет собой универсальное, наиболее рациональное множество. Исходя из полноты представления формируемых требований к системе, объединим в группы требования уровней k и (k+1) каждой i-й группы, используя операцию примитивного синтеза: FS(p, q)®C, присоединяющую элемент pÎA Результатом объединения требований, поступивших на k-м и (k+1)-м этапах, являются сформированные требования к системе С, то есть множество требований AiÌC, BiÌC, C=AiÈBi. Подобная поэтапная методика формирования требований не позволит упустить ключевые точки процесса разработки сложных информационных систем. Однако не следует допускать формирование избыточности требований. Чем больше множество требований на (k+1)-м этапе, тем больше вероятность избыточности и повторения требований. Часть пространства параметров и признаков, соответствующую пересечению подмножеств требований от разных этапов, можно интерпретировать как область неопределенности. При этом подмножество избыточных требований X будет следующим: XÍAiÇBi. Разрешение неопределенности возможно путем уменьшения избыточности. В идеале неопределенность не влияет, когда Тогда мощность подмножества ошибки Ол, то есть подмножества сформированных избыточных требований cardOл®min, и количество требований åpi®min уменьшаются. Это говорит о том, что для исключения избыточности необходимо, чтобы формируемые множества содержали в себе небольшое количество единичных требований. Достичь этого можно, найдя оптимальный баланс при правильном построении и формировании единичного требования и выделении важных и полезных требований, исключающих перегруженность программы. Таким образом, подмножества требований на каждом из этапов не должны пересекаться, но при этом каждое из них должно принадлежать соответствующему элементу множества требований, существующему в течение нескольких этапов. Необходимо, чтобы алгоритм формирования требований обеспечивал выявление этой принадлежности: Агрегирование требований должно обеспечить выделение компактных модульных групп требований, представление их эталонами, в наибольшей степени связанными с другими составляющими своей группы и удаленными от соседних групп (что позволит сократить время решения задач активным средством), а также исключение избыточности требований в группах. Литература 1. Royce Winston W. Managing the Development of Large Software Systems. Proceedings of IEEE Wescon. 1970, august, pp. 1–9. 2. Халл Э., Джексон К., Дик Дж. Разработка и управление требованиями. Практическое руководство пользователя. URL: www.springeronline.com (дата обращения: 15.12.2009). 3. Горелик А.В., Скрипин В.А. Методы распознавания. М.: Высш. шк., 1989. 4. Крылов С.М. Алгоритмы, математика эволюции и технологии будущего. М.: ЛКИ, 2008. 5. Заде Л.А. Понятие лингвистической переменной и его применение к принятию приближенных решений. М.: Мир, 1976. 164 с. |
| Permanent link: http://swsys.ru/index.php?id=2522&lang=en&page=article |
Print version Full issue in PDF (4.97Mb) Download the cover in PDF (1.38Мб) |
| The article was published in issue no. № 2, 2010 |
Perhaps, you might be interested in the following articles of similar topics:
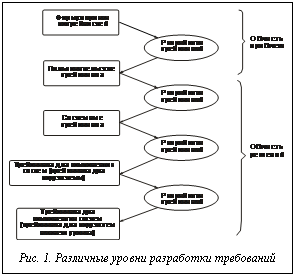 Она сохраняет упорядоченность каскадной модели, не теряя гибкости и творческой ориентации модели спиральной. При этом общие подходы к разработке требований к проектируемой системе предполагают их формирование и уточнение на каждом уровне проектирования (рис. 1). При многоуровневой разработке каждый уровень требует соответствующих знаний и опыта. На верхнем уровне очень важно знание предметной области, которая соответствует проблеме, а на системном – получение общего представления о системе, чтобы избежать узкого и слишком детализированного понимания пользовательских требований. На этом уровне непременно появляется уклон в сторону определенного решения.
Она сохраняет упорядоченность каскадной модели, не теряя гибкости и творческой ориентации модели спиральной. При этом общие подходы к разработке требований к проектируемой системе предполагают их формирование и уточнение на каждом уровне проектирования (рис. 1). При многоуровневой разработке каждый уровень требует соответствующих знаний и опыта. На верхнем уровне очень важно знание предметной области, которая соответствует проблеме, а на системном – получение общего представления о системе, чтобы избежать узкого и слишком детализированного понимания пользовательских требований. На этом уровне непременно появляется уклон в сторону определенного решения.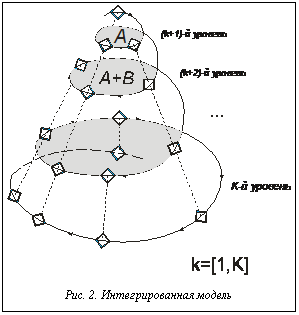 Требования к программному продукту (основополагающий класс требований) формулирует заказчик. Цель, которую он преследует, – получить хороший, функциональный и удобный в использовании конечный продукт. Заказчик, вступая в договорные отношения с разработчиком, несет различные риски, главным из которых является получение продукта с опозданием либо ненадлежащего качества. Основные мероприятия по контролю и снижению риска – регламентация процесса создания программного обеспечения и его аудит. При регламентировании требований к проекту необходимо учесть множество факторов, таких как ценность конечного продукта для заказчика, степень доверия заказчика к разработчику, сумма подписанного контракта, увязка срока сдачи продукта в эксплуатацию с бизнес-планами заказчика и т.д.
Требования к программному продукту (основополагающий класс требований) формулирует заказчик. Цель, которую он преследует, – получить хороший, функциональный и удобный в использовании конечный продукт. Заказчик, вступая в договорные отношения с разработчиком, несет различные риски, главным из которых является получение продукта с опозданием либо ненадлежащего качества. Основные мероприятия по контролю и снижению риска – регламентация процесса создания программного обеспечения и его аудит. При регламентировании требований к проекту необходимо учесть множество факторов, таких как ценность конечного продукта для заказчика, степень доверия заказчика к разработчику, сумма подписанного контракта, увязка срока сдачи продукта в эксплуатацию с бизнес-планами заказчика и т.д. .
. – это универсальное множество, то есть полное множество, охватывающее проблемную область в момент создания системы (на k-м уровне) в i-й группе.
– это универсальное множество, то есть полное множество, охватывающее проблемную область в момент создания системы (на k-м уровне) в i-й группе. единицами требований.
единицами требований. к объединенному множеству требований.
к объединенному множеству требований. ®0 при k=[1, K], где K – количество этапов формирования требований к системе.
®0 при k=[1, K], где K – количество этапов формирования требований к системе. .
.