Journal influence
Bookmark
Next issue
Modelling robot’s interaction with external environment on the basis of spatial logics and constraints propagation
The article was published in issue no. № 2, 2010Abstract:The evolution of robots generations is analyzed. The necessary requirements to develop 4th generation robots as cognitive agents are formulated. It is shown that an important property of cognitive agent is situative information granulation enabling the work under uncertainty. In the context of constructing spatial granules a static spatial logic is introduced to model robot’s interaction with external environment. It is based on combining Pospelov’s pseudophysical logics with Zadeh’s generalized constraints. Some versions of fuzzy linguistic constraints propagation for the problems of spatial situation analysis are investigated.
Аннотация:Проанализирована эволюция поколений роботов, сформулированы требования к роботам четвертого поколения как когнитивным агентам. Показано, что важнейшим качеством когнитивного агента является ситуативное гранули-рование информации, необходимое для работы в условиях неопределенности. В контексте построения пространст-венных гранул введена статическая пространственная логика для моделирования взаимодействия робота с внешней средой. Исследованы варианты распространения нечетких лингвистических ограничений в задачах анализа про-странственной ситуации.
| Authors: (k_a_p@rbcmail.ru) - , V.B. Tarasov (vbulbov@yahoo.com) - Bauman Moscow State Technical University (Associate Professor), Moscow, Russia, Ph.D | |
| Keywords: distance and orientation logic, spatial logics, generalized constraints, pseudophysical logics, cognitive robot, robot-environment interaction, environment, autonomous agent |
|
| Page views: 11892 |
Print version Full issue in PDF (4.97Mb) Download the cover in PDF (1.38Мб) |
Проблема моделирования взаимодействия искусственных агентов с внешней средой является одной из центральных при создании и использовании агентно-ориентированных технологий в различных областях: от мобильных софтботов, перемещающихся в сети Интернет, до автономных роботов, функционирующих в экстремальных средах, или многоагентных комплексов, входящих в состав интеллектуальных производств. Искусственный агент представляет собой автономную, открытую систему, помещенную в некоторую среду, причем эта система обладает собственным поведением, удовлетворяющим некоторым экстремальным принципам [1]. Минимальный набор базовых характеристик агента, отличающих его от обычных объектов информатики и искусственного интеллекта, включает такие свойства, как активность, реактивность, автономность, общительность и целенаправленность. В статье рассматриваются индивидуальные, физические, мобильные, автономные агенты. Примерами таких агентов служат интеллектуальные роботы, функционирующие в экстремальных средах. Здесь ключевую роль играет моделирование взаимодействия робота со средой, и в первую очередь, описание процесса комплексирования информации, поступающей на датчики (сенсоры) робота, а также диалога человека-пользователя с роботом на ограниченном естественном языке [2]. Соответствующее отношение моделирования [3] является нечетким, то есть отображает полиморфное соответствие между компонентами физического и ментального мира робота. На пути к когнитивным роботам В работах [4, 5] описаны три поколения роботов: промышленные, очувствленные, интегральные. Роботы первого поколения работают в простом, строго фиксированном внешнем мире, соответственно, модель внешней среды у них отсутствует. Как следствие, управляющая программа является жесткой, и ее надо менять даже тогда, когда меняется положение хотя бы одного объекта в сфере действия промышленного робота. Конечно, промышленные роботы не имеют автономности. Роботы второго поколения уже являются очувствленными, то есть снабжены системой тактильных датчиков, позволяющих воспринимать информацию о мире. Внешний мир роботов второго поколения уже не фиксирован строго, поэтому у них появляются простейшие, одношаговые планы, которые в основном сводятся к подстановке конкретных координат в программу с параметрами. Роботы этого поколения также не обладают автономностью. Роботы третьего поколения называются интегральными (этот термин был предложен Н. Нильсоном) и обладают некоторой степенью интеллектуальности. Для определения понятия «интегральный робот» обычно используют следующие пять групп робототехнических устройств: 1) системы восприятия зрительной, слуховой, тактильной и других типов информации о внешнем мире; 2) системы воздействия на объекты внешнего мира – манипуляторы, педипуляторы и пр.; 3) системы, обеспечивающие перемещение робота, – колесные, гусеничные, шагающие, плавающие, летающие движители и аппараты; 4) системы целеполагания и планирования действий робота, системы решения задач; 5) системы, обеспечивающие коммуникацию робота с человеком-оператором и другими роботами на языках общения различных уровней вплоть до естественного языка. Любой конкретный робот сочетает в себе системы, принадлежащие указанным группам. Это позволяет классифицировать роботы третьего поколения по степени интеграции и набору входящих в них систем.
Роботы четвертого поколения должны быть способными работать в открытых динамических мирах, строить сложные многоцелевые планы поведения, определяемые оценкой внешней ситуации и внутренней мотивацией робота [4]. Следовательно, можно утверждать, что роботы нового поколения имеют статус когнитивного агента. Когнитивная функция обеспечивает процессы познания роботом внешнего мира, других агентов, а также самопознание. При этом ос- новными когнитивными процессами являются восприятие среды, построение ее обобщенного представления, понимание закономерностей взаимодействия и поведения. Сюда же относятся процессы распределения ресурсов (в частности внимания), прогнозирования и планирования поведения, формирования рассуждений о собственных состояниях и состояниях других объектов и агентов. Таким образом, когнитивный робот должен иметь БЗ, встроенный механизм мотивации и целеобразования (или интерпретации целей пользователя), возможность формирования своих мнений и предпочтений по выполняемой задаче, способность перемещаться в реальном физическом мире и выполнять как рабочие, так и гностические (познавательные) движения. Подобные роботы в первую очередь требуются для функционирования в экстремальных средах. На взгляд авторов, важнейшей характеристикой когнитивного робота должна быть способность к гранулированию информации – формированию информационных «зерен» различной точности. Гранулой называется семейство объектов, связанных между собой либо функционально, либо отношениями сходства, эквивалентности или неразличимости. Гранулярные (приближенные) структуры обычно противопоставляются сингулярным (точным, одноэлементным): различия между ними подчас интерпретируются как различия между данными и уровнями знаний (величинами гранул). Примером простейшей операции грануляции служит разбиение целого на части (в общем случае приближенное и нечеткое). Классическими примерами математических гранулярных структур служат интервалы, распределения, приближенные множества, нечеткие множества. При создании когнитивных роботов следует в первую очередь реализовать в них процедуры гранулирования пространства и времени. В частности, речь идет о построении модели внешней среды робота с использованием естественных пространственных отношений. В данной работе для этого используются псевдофизические пространственные логики вместе с обобщенными ограничениями. Псевдофизические логики и обобщенные ограничения Логико-лингвистические методы описания когнитивных роботов основаны на том, что поведение робота выражается в терминах ограниченного естественного языка и может быть представлено с помощью лингвистических переменных. При этом последние используются в качестве пропозициональных переменных псевдофизических логик (ПФЛ). Под ПФЛ понимается логика, отражающая восприятие агентом закономерностей внешней физической среды [6]. Примерами ПФЛ являются временные логики, пространственные, логики действий и т.п. В целом ПФЛ можно охарактеризовать как логики отношений; логики на шкалах; логики, которые в качестве аксиом содержат утверждения, вытекающие из восприятия мира человеком, причем эти утверждения должны быть обоснованы результатами соответствующих психологических экспериментов; неклассические, многозначные, нечеткие, лингвистические логики. Псевдофизическая логическая система представляет собой семейство взаимосвязанных логических подсистем, которые можно отнести к двум основным уровням. На первом уровне находятся пространственная, временная, каузальная логика, а также логика движений и действий. На втором, более высоком уровне находятся логики мнений, целей, оценок, норм и пр. Логики первого уровня непосредственно связаны с взаимодействием роботов с внешней средой. Отметим, что ПФЛ тесно связаны с понятием нечеткого отношения моделирования [3]. Пусть среда, в которой находится робот, характеризуется множеством состояний W={w1, …, wm}. Будем характеризовать представление роботом среды с помощью нечеткого отображения c: W Таблица 1
В настоящей работе предложены варианты построения ПФЛ с помощью обобщенных ограничений (а не разнородных отношений), что обеспечивает единый подход к описанию неопределенностей при взаимодействии агента с внешней средой и существенно упрощает инженерную реализацию агентно-ориентированных технологий в робототехнике. Обобщенное ограничение [7] имеет вид: GC(X)=X isr R, где X – переменная, принимающая значение на универсуме U; R – гибкое ограничение на эту переменную; isr – переменная связка, в которой r является переменной, а ее значение определяет способ, которым R ограничивает X (то есть тип ограничения и его семантику). Пространственные логики Пространственные логики подразделяются на статические и динамические. Статические пространственные логики позволяют описывать закономерности взаимного расположения объектов в пространстве с учетом расстояний между ними, ориентации объектов относительно друг друга и размеров объектов при их расположении в пространстве. Динамические пространственные логики позволяют определить величину и направление скорости движения робота и описать траекторию перемещения робота в пространстве. При разработке интеллектуальных роботов, имеющих специальные устройства для получения информации о внешнем мире (объектах, расположенных в нем), возникает проблема создания описания пространственной ситуации вокруг робота по информации, полученной от человека-оператора на ограниченном естественном языке (рис. 1). Пространственные отношения. В пространственных логиках для робототехнических систем следует использовать нечеткие бинарные пространственные отношения трех типов: отношения для расстояний, для направлений, отношения взаимного расположения объектов.
Взаимная угловая ориентация между объектами обычно определяется с помощью базовых направлений, связанных с системой координат наблюдателя. В самом простом случае это впереди–сзади и справа–слева [6]. Их комбинация дает восемь базовых отношений для направлений, и лингвистическая переменная «Направление» принимает значения fi, i=1, 2, …, 8, где f1 – впереди, f2 – впереди и слева, f3 – слева и т.д. Взаимное положение объектов можно представить конъюнкцией обобщенных ограничений на расстояние и ориентацию: [X(a1; a2) is dj] & [X(a1; a2) is fj]=[X(a1; a2) is dj] is fj. Например, отношение «робот а находится далеко и справа от объекта b» можно записать как [X(a; b) is d4]&[X(a; b) is f7] = [X(a; b) is d4] is f7. Статическая пространственная логика. Главную роль в организации нечетких пространственных рассуждений робота на основе теории ограничений Л. Заде играет распространение нечетких ограничений от посылок к заключениям. В частности, «если робот а находится рядом с роботом b, а тот держит схватом объект с, то робот а находится вблизи объекта с». Несомненный интерес представляет построение рассуждений на основе системы связанных между собой неоднородных ограничений, в частности, относящихся к лингвистическим переменным «Расстояние» и «Размер». Гипотеза о влиянии размеров объектов на оценку оператором расстояния между ними [6] позволяет производить замену пространственных отношений для расстояний на размеры объектов и наоборот в соответствии с таблицей 2. Таблица 2
Например, «если робот а находится близко от объекта b, а между объектами b и c расположен объект очень большого размера (скажем, здание), то робот а находится не далеко и не близко от объекта с». Рассмотрим частный случай расположения объектов на плоскости, когда они находятся на одной прямой. Правила вывода для полного анализа отношений между объектами должны связывать между собой цепочки из трех объектов. Схема вывода, связанная с распространением нечетких лингвистических ограничений, имеет вид:
Если размеры объектов a1 и a2 не совпадают, необходимо, используя связь между размерами объектов и отношением расстояния, перейти к объектам с одинаковым размером. Порядковый номер нового отношения расстояния определяется по формуле j*=i+x–y, где i, j, x, y – порядковые номера отношений расстояния и размеров объектов (столбец 1 в табл. 1). В результате получим схему распространения нечетких лингвистических ограничений:
Рассмотрим случай, когда объекты расположены на одной плоскости (рис. 2). Из взаимосвязи размеров объектов и отношений расстояния следует, что достаточно построить логику на плоскости для произвольно расположенных точечных объектов. Отношения расстояния между объектами различных размеров могут быть получены с помощью правила соотнесения размеров и расстояний. Для упрощения вычислений на плоскости направления фиксированы и их количество ограничено количеством введенных отношений для взаимной угловой ориентации объектов. Другими словами, будем считать, что объект a3 может находиться только на этих восьми фиксированных направлениях. На рисунке 2 изображены три точечных объекта на плоскости. Примем объект a2 за точку отсчета. Проведем окружность с центром в точке a2 и радиусом dj для фиксации направлений на плоскости. Схема вывода имеет вид
Для определения расстояний рассмотрим объекты, которые находятся на пересечении этой окружности с вертикальной прямой. Из рисунка 2 видно, что искомое отношение удовлетворяет неравенству dmin£d?£dmax. Для получения d? воспользуемся тем, что в построенной модели пространства направления фиксированные. Для объектов, изображенных на рисунке 2, получим Таблица 3
Построенная логика на плоскости позволяет выводить новые пространственные отношения расстояния, являющиеся функцией направления. Проиллюстрируем работу построенной логики на примере. Пусть имеется гибкий производственный модуль (ГПМ), содержащий станок и робот-манипулятор, а также автономный робокар, который, перемещаясь между складом и ГПМ, обеспечивает модуль заготовками. Пусть пространственное положение компонентов данной гибкой производственной системы описывается в виде: «Впереди, не далеко и не близко от робокара расположен ГПМ 1, очень близко и справа от ГПМ 1 находится ГПМ 2. Близко и сзади, справа от ГПМ 2, размещен склад заготовок для ГПМ 1, 2» (рис. 3). Введем обозначения: a1 – робокар; a2 – ГПМ 1; a3 – ГПМ 2; a4 – склад. В соответствии с этим для значений лингвистических переменных «Расстояние» и «Направление» (табл. 1) получим исходные ограничения:
С помощью распространения ограничений получим новые факты для пространственной ситуации робокара: Таким образом, построенная пространственная логика на плоскости позволяет выводить дополнительные нечеткие пространственные ограничения, не описанные человеком явно. В заключение можно сделать выводы о перспективах применения ПФЛ в робототехнике, которые не ограничиваются задачей построения пространственной или пространственно-временной модели внешней среды. Несомненно, они тесно связаны с планированием поведения и организацией действий робота, и в первую очередь, с организацией диалогового управления [2], когда между партнерами (человеком и роботом) ведется диалог на ограниченном естественном языке, в ходе которого у последнего формируется достаточный уровень понимания проблемы, поставленной пользователем. Литература 1. Тарасов В.Б. От многоагентных систем к интеллектуальным организациям. М.: Эдиториал УРСС, 2002. 2. Ющенко А.С. Диалоговое управление роботами с использованием нечетких моделей // Интегрированные модели и мягкие вычисления в искусственном интеллекте: сб. тр. V Междунар. науч.-практич. конф. (Коломна, 28–30 мая 2009 г.). М.: Физматлит, 2009. Т. 1. С. 97–108. 3. Аверкин А.Н., Тарасов В.Б. Нечеткое отношение моделирования и его применение в психологии и искусственном интеллекте. М.: ВЦ АН СССР, 1986. 4. Попов Э.В., Фирдман Г.Р. Алгоритмические основы интеллектуальных роботов и искусственного интеллекта. М.: Наука, 1976. 5. Добрынин Д.А. Интеллектуальные роботы вчера, сегодня, завтра // КИИ-2006: тр. 10-й национальной конф. по искусствен. интел. (25–28 сентября 2006 г., Обнинск). М.: Физматлит, 2006. Т. 1. С. 20–32. 6. Кандрашина Е.Ю., Литвинцева Л.В., Поспелов Д.А. Представление знаний о времени и пространстве в интеллектуальных системах. М.: Наука, 1989. 7. Zadeh L.A. Toward a Generalized Theory of Uncertainty (GTU): an Outline // Information Sciences – Informatics and Computer Science. 2005. Vol. 172. № 1–2, pp. 1–40. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Permanent link: http://swsys.ru/index.php?id=2528&lang=en&page=article |
Print version Full issue in PDF (4.97Mb) Download the cover in PDF (1.38Мб) |
| The article was published in issue no. № 2, 2010 |
Perhaps, you might be interested in the following articles of similar topics:
 Согласно [4], уровень интеллектуальности робота оценивают по следующим параметрам: сложность и динамичность внешней среды; богатство восприятия роботом информации о внешней среде; гибкость планирующей и управляющей систем робота; степень его автономности. Но главный признак интеллектуальности – наличие развитой модели внешней среды (динамической БЗ), что позволяет роботу действовать в условиях неопределенности. Общая структура интеллектуального робота представлена на рисунке 1.
Согласно [4], уровень интеллектуальности робота оценивают по следующим параметрам: сложность и динамичность внешней среды; богатство восприятия роботом информации о внешней среде; гибкость планирующей и управляющей систем робота; степень его автономности. Но главный признак интеллектуальности – наличие развитой модели внешней среды (динамической БЗ), что позволяет роботу действовать в условиях неопределенности. Общая структура интеллектуального робота представлена на рисунке 1. M, которое ставит в соответствие некоторому элементу среды wÎW нечеткое множество элементов ее внутренней модели mÎM, или, что одно и то же, с помощью нечеткого отношения моделирования R: W´M®[0, 1]. Отношение моделирования удобно записать в виде матрицы размером m´n, где на пересечении столбца wi, i=1,…, m, и строки mj, j=1, …, n, находится число mR(wi, mj). Это число представляет собой коэффициент соответствия между данным состоянием среды, например, «расстояние 2 м от робота до препятствия», и его внутренним представлением роботом в виде лингвистического значения «малое». Пример матрицы нечеткого отношения моделирования для ситуации приближения интеллектуального робота к препятствию приведен в таблице 1.
M, которое ставит в соответствие некоторому элементу среды wÎW нечеткое множество элементов ее внутренней модели mÎM, или, что одно и то же, с помощью нечеткого отношения моделирования R: W´M®[0, 1]. Отношение моделирования удобно записать в виде матрицы размером m´n, где на пересечении столбца wi, i=1,…, m, и строки mj, j=1, …, n, находится число mR(wi, mj). Это число представляет собой коэффициент соответствия между данным состоянием среды, например, «расстояние 2 м от робота до препятствия», и его внутренним представлением роботом в виде лингвистического значения «малое». Пример матрицы нечеткого отношения моделирования для ситуации приближения интеллектуального робота к препятствию приведен в таблице 1. Так, отношения для расстояний обычно имеют исходные значения «близко–далеко», на основе которых строятся составные значения «очень близко», «довольно далеко» и пр. Соответственно, значения лингвистической переменной «Расстояние между объектами а и b» ограничиваются функциями принадлежности (распределениями возможности). Эти распределения получены в результате оценки дистанции человеком-оператором; их можно записать в виде нечеткого лингвистического ограничения: X(a, b) is dj, где dj – термы лингвистической переменной «Расстояние»: d0 – вплотную, d1 – очень близко, d2 – близко и т.д. (в соответствии с табл. 1). Каждое такое ограничение образует гранулу. Возможность изменения размеров и центров гранул позволяет изменять степень точности описания пространственной ситуации.
Так, отношения для расстояний обычно имеют исходные значения «близко–далеко», на основе которых строятся составные значения «очень близко», «довольно далеко» и пр. Соответственно, значения лингвистической переменной «Расстояние между объектами а и b» ограничиваются функциями принадлежности (распределениями возможности). Эти распределения получены в результате оценки дистанции человеком-оператором; их можно записать в виде нечеткого лингвистического ограничения: X(a, b) is dj, где dj – термы лингвистической переменной «Расстояние»: d0 – вплотную, d1 – очень близко, d2 – близко и т.д. (в соответствии с табл. 1). Каждое такое ограничение образует гранулу. Возможность изменения размеров и центров гранул позволяет изменять степень точности описания пространственной ситуации.

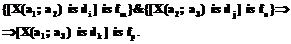
 Для построения логики на плоскости первоначально определим правила для вывода направлений, так как расстояния между объектами зависят от угловой ориентации объектов. Построим правила вывода для направлений по заданным направлениям для двух объектов относительно третьего [7]. Они имеют вид
Для построения логики на плоскости первоначально определим правила для вывода направлений, так как расстояния между объектами зависят от угловой ориентации объектов. Построим правила вывода для направлений по заданным направлениям для двух объектов относительно третьего [7]. Они имеют вид
 Рассматривается только одна полуплоскость, так как вторая симметрична первой: n*=n(dmax–n(dmin), где n(dmax), n(dmin) – порядковый номер отношений расстояния, определенный по таблице 3 в зависимости от отношения направления. Операция «–» обозначает уменьшение порядкового номера отношения расстояния.
Рассматривается только одна полуплоскость, так как вторая симметрична первой: n*=n(dmax–n(dmin), где n(dmax), n(dmin) – порядковый номер отношений расстояния, определенный по таблице 3 в зависимости от отношения направления. Операция «–» обозначает уменьшение порядкового номера отношения расстояния.
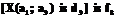 , так как n(d3) – n(d1)=2³2, dmax=dmin=d3;
, так как n(d3) – n(d1)=2³2, dmax=dmin=d3;  так как n*=n(dmax=d4)–n(dmin=d1)=3; далее по таблице 2 находим d(f4), потому что направление f6 симметрично направлению f4.
так как n*=n(dmax=d4)–n(dmin=d1)=3; далее по таблице 2 находим d(f4), потому что направление f6 симметрично направлению f4.