Software & Systems

Для проектирования микросхем, стойких к одиночным событиям, разработано проблемно-ориентированное программное обеспечение, позволяющее учесть радиационные эффекты от одиночных ядерных частиц (ОЯЧ).

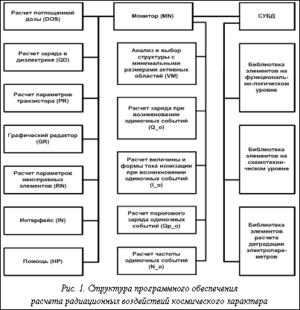Оно является одной из подсистем программного обеспечения, с помощью которого рассчитывается стойкость изделий к факторам космического происхождения. На рисунке 1 приведена структура подсистемы расчета стойкости сверхбольших интегральных схем (СБИС) к факторам космического пространства.

Основное внимание при разработке данного программного обеспечения уделялось созданию математических моделей, позволяющих учесть воздействие ОЯЧ, а для решения задач собственно моделирования на различных уровнях адаптированы известные средства функционально-логи­ческого моделирования и генерации тестов, схемотехнического, топологического проектирования.

При адаптации указанных средств проведена их модификация с целью повышения эффективности и в первую очередь снижения вычислительных затрат для обеспечения решения задач моделирования базовых элементов в реальном времени.

Алгоритм процесса моделирования сбора заряда предложено свести к решению упрощенной задачи, основанной на следующих предположениях.

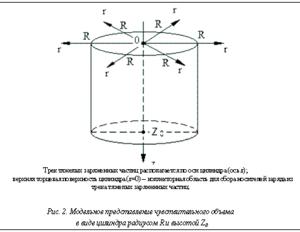
Во-первых, чувствительный объем представляется в виде цилиндра, по оси которого проходит трек тяжелых заряженных частиц. Вдоль оси цилиндра направлена координатная ось z. Заряд, генерированный в треке, собирается коллекторной областью, которой является верхняя торцевая поверхность цилиндра. В начальный момент задается радиальное распределение носителей заряда в треке, а дальше рассматривается эволюция трека с учетом объемной рекомбинации носителей заряда.

Во-вторых, предполагается отсутствие внешнего поля. Таким образом, рассматривается только заряд, собранный посредством диффузии. Учет дрейфовой составляющей, как это описывалось выше, может быть осуществлен, например, путем удвоения диффузионного тока неосновных носителей.

В-третьих, объемная рекомбинация определяется двумя механизмами: Оже-рекомбиницией и рекомбинацией Шокли–Рида–Холла. Общая скорость объемной рекомбинации R будет складываться из скоростей этих двух видов рекомбинации:

.                                                 (1)

Для скорости Оже-рекомбинации RAuger можно записать как

                 (2)

где n, р – полные концентрации носителей; n0, р0 – начальные равновесные концентрации носителей.

Значения Оже-коэффициентов Ce и Сh для кремния обычно составляют порядка 2×10–31 см6/с.

Для скорости рекомбинации Шокли–Рида–Холла RSRH можно записать как

,                          (3)

где  – время жизни электронов и дырок (при низком уровне инжекции); vthn, vthp – тепловая скорость электронов и дырок соответственно; sn, sp – сечение захвата электронов и дырок соответственно.

Для низкого уровня инжекции (когда доминирует механизм рекомбинации Шокли–Рида–Холла) можно приблизительно считать, что скорость рекомбинации определяется выражением

,                                         (4)

где tpl=tnl=t.

В-четвертых, предполагается наличие аксиальной симметрии относительно оси z (направление начального трека). Если использовать цилиндрическую систему координат, то данное предположение позволяет превратить решаемую задачу из трехмерной в двухмерную относительно независимых координат z и r (рис. 2). Плотность носителей заряда не будет зависеть от полярного угла в силу наличия аксиальной симметрии относительно оси z.

При этих предположениях уравнения диффузии для неравновесных носителей заряда, генерированных в треке тяжелых заряженных частиц, можно записать в виде

,                                                   (5)

,                                                   (6)

где Dp, Dn – коэффициенты диффузии электронов и дырок.

Общий ток, характеризующий значение собранного заряда, определяется диффузионным током неосновных носителей заряда, значение которого умножается на коэффициент порядка 2 для учета дрейфовой компоненты. Известно, что обычно в качестве чувствительной области, отвечающей за возникновение одиночных обратимых сбоев при воздействии тяжелых заряженных частиц, выступает область пространственного заряда стокового p-n-перехода закрытого n-канального транзистора. Если считать, что уровень легирования n+-стоковой области значительно выше, чем в р-подложке, то область пространственного заряда будет практически полностью сосредоточена в подложке. Следовательно, в качестве неосновных носителей заряда можно рассматривать электроны, изменение концентрации которых описывается уравнением (6).

Следует учесть, что при высоком уровне инжекции коэффициенты диффузии для электронов и дырок в уравнениях (5) и (6) будут равны коэффициенту амбиполярной диффузии. В качестве границы между высоким и низким уровнями инжекции можно принять равенство концентраций избыточных неосновных носителей (электронов) и основных носителей заряда (дырок): n–n0=p0. Если концентрация избыточных электронов превышает равновесную концентрацию дырок, реализуется состояние с высоким уровнем инжекции, иначе – с низким.

В качестве граничных условий можно принять:

;                                                              (7)

;                                                            (8)

;                                               (9)

;                                                                 (10)

;                                                            (11)

.                                                (12)

Начальное распределение плотности носителей заряда можно найти из начального распределения поглощенной энергии в треке тяжелых заряженных частиц, которое в общем случае не является однородным (в некоторых работах указывается, что распределение поглощенной энергии в треке пропорционально 1/r2, где r – расстояние от трека). Однако во многих случаях можно пренебречь неоднородным распределением поглощенной энергии в треке, поскольку начальный радиус трека намного меньше размеров области сбора заряда, для которой решается задача. Типичное значение начального радиуса трека составляет порядка 0,1 мкм, отсюда площадь поперечного сечения трека ~0,03 мкм2. Как уже указывалось, чувствительной областью для эффектов одиночных сбоев является область пространственного заряда стокового перехода закрытого n-канального транзистора. Размеры стоковой области можно определить, если известна топология базового элемента СБИС. Рассмотрим топологию с проектными нормами 350 нм. В соответствии с правилами проектирования транзисторы бывают трех типов: А-типа, Н-типа и с параллельно соединенными стоками.

Если считать, что напряжение на стоке закрытого n-канального транзистора в КМОП-паре равно напряжению питания, и взять его равным 5 В, то ширина области пространственного заряда составит порядка 0,8–2,6 мкм в зависимости от уровня легирования р-подложки (данные оценки получены для концентрации акцепторной примеси в р-подложке 1016 и 1015 см–3). При этом площадь чувствительной области, определяемая площадью области пространственного заряда стокового перехода n-канального транзистора, составит 48–112 мкм2. Как видно, данные значения существенно превосходят площадь поперечного сечения исходного трека тяжелых заряженных частиц. Это позволяет пренебречь неоднородностью распределения плотности носителей заряда по толщине трека.

Если считать, что длина пробега тяжелых заряженных частиц значительно превышает глубину области сбора заряда, в результате в пределах этой области можно пренебречь изменением линейной потери энергии (ЛПЭ) по длине трека (такая ситуация реализуется при длине пробега тяжелых заряженных частиц порядка 30–40 мкм и более), то концентрацию электронно-дырочных пар ne-h в треке можно оценить следующим образом:

,                                       (13)

где DE – энергия, поглощенная на участке трека длиной Dz; ei – энергия ионизации (для Si ei»3,6 эВ); DV – объем участка трека длиной Dz.

Если линейные потери энергии тяжелых заряженных частиц L считать приблизительно постоянными, то для них можно записать

.                                                (14)

С учетом (14) выражение (13) принимает вид:

.                                                         (15)

Начальные концентрации электронов и дырок в треке принимаются равными концентрации электронно-дырочных пар, определяемой формулой (15).

Таким образом, алгоритм моделирования сбора заряда из трека тяжелых заряженных частиц в случае нормального падения тяжелых заряженных частиц по центру области сбора заряда проводится следующим образом.

1.                             Решается краевая задача для распределений концентрации носителей заряда в чувствительном объеме

           (16)

          (17)

; ;                   (18)

;                   (19)

        (20)

                                  (21)

                                  (22)

Данная задача решается численно для различных значений ЛПЭ падающих частиц, которые определяют начальную концентрацию электронно-дырочных пар в треке.

2. Вычисляется диффузионный ток неосновных носителей заряда (электронов) через верхнюю торцевую поверхность цилиндрического чувствительного объема:

.                                      (23)

В полярной системе координат с учетом аксиальной симметрии относительно оси z выражение (23) можно преобразовать:

.                           (24)

3. Общий ток неосновных носителей, учитывающий дрейфовую компоненту, определяется путем удваивания диффузионного тока:

.               (25)

4. Собранный заряд определяется путем интегрирования выражения (25):

.           (26)

Таким образом, предлагаемая методика позволяет рассчитать для заданного значения ЛПЭ падающих частиц форму импульса ионизационного тока (точнее, его диффузионной составляющей) и зависимость собранного заряда от времени после попадания частицы. При вычислении собранного заряда необходимо корректно выбрать верхний предел интегрирования в интеграле по времени. В частности, можно взять такое значение t в качестве верхнего предела интегрирования, при котором остаток составит не более 10 % от общего значения заряда.

После того как получена зависимость собранного заряда от значения ЛПЭ тяжелых заряженных частиц, может быть определено пороговое значение ЛПЭ тяжелых заряженных частиц для одиночных обратимых сбоев. В качестве порогового выбирается такое значение ЛПЭ, при котором собранный заряд равен заряду переключения логического состояния КМОП-триггера, для которого проводится моделирование. Величина заряда переключения обычно известна, как правило, она рассчитывается на этапе разработки конструкции и технологии СБИС.

Для предсказания частоты и вероятности возникновения одиночных сбоев при воздействии тяжелых заряженных частиц с заданными спектрально-энергетическими характеристиками, кроме порогового значения ЛПЭ L0, необходимо также знать значение сечения насыщения s0. Если известны эти два параметра, можно воспользоваться, например, рекомендациями РД В 319.03.38-2000 для определения значений остальных параметров функции Вейбулла, аппроксимирующей зависимость сечения сбоев от ЛПЭ, и рассчитать частоту сбоев по формуле

,                                    (27)

где jion(L) – дифференциальный ЛПЭ-спектр тяжелых заряженных частиц, см–2с–1(МэВ×см2/мг)–1; s(L) – зависимость сечения событий от ЛПЭ тяжелых заряженных частиц, которая обычно аппроксимируется функцией Вейбулла.

В качестве s0 можно принять площадь торцевой поверхности цилиндрического чувствительного объема, для которого проводилось моделирование сбора заряда:

s0 = pR2.                                                                (28)

Можно также воспользоваться известным соотношением, характерным для статических ОЗУ, между площадью запоминающей ячейки SЗЯ и топологической нормой проектирования lT

SЗЯ [мкм2] » 300(lT [мкм])2                               (29)

и считать сечение насыщения равным площади запоминающей ячейки. Такой подход будет давать завышенное значение s0, следовательно, завышенное значение частоты возникновения событий, однако относительно обеспечения стойкости изделий к эффектам одиночного события это является вполне оправданным.

Следует также отметить, что при вычислении частоты возникновения событий по формуле (27) берется сечение сбоев, приходящееся на корпус. Для этого сечение одной запоминающейся ячейки умножается на информационную емкость (общее количество бит) моделируемой СБИС. После этого проводится предварительное формирование результатов расчета. Оно заключается во включении в БД результатов расчета четырех составляющих: порогового значения энергии и массивов тока ионизации, частоты сбоев, сечения в зависимости от энергии тяжелых заряженных частиц.

Отметим, что оценка стойкости СБИС к воздействию тяжелых заряженных частиц в полном виде включает в себя определение оценки времени потери работоспособности СБИС и пороговой энергии наступления тиристорного эффекта, если он наблюдается. Однако очень часто проектировщику аппаратуры достаточно знать пороговое значение энергии и зависимости сечения и частоты сбоев от энергии частиц при условии, что тиристорный эффект отсутствует. Поэтому, как правило, расчет на этом заканчивается. Необходимо только оценить его адекватность и, если точность расчета вписывается в допустимые нормы, сформировать результаты для окончательного вывода.

Разработанная подсистема позволяет проводить расчет параметров внешней среды (радиационного воздействия), изменения параметров моделей стандартных элементов при воздействии статических видов радиации космического характера – электронного и протонного излучений, характерных для космического пространства.

Программное обеспечение радиационного моделирования включает модули:

·     монитора – центрального звена средств моделирования, который обеспечивает взаимодействие всех программных модулей, а также выход на операционную систему;

·     расчета накопленной дозы, определяющего характеристики внешней среды;

·     расчета заряда в подзатворном диэлектрике, который накапливается при воздействии статических факторов космического пространства;

·     расчета параметров моделей транзистора для схемотехнического моделирования с использованием Spice-подобных программ.

Полученные значения параметров транзисторов соответствуют их деградации при воздействии данной дозы радиации. Данные об элементах заносятся в БД. Они относятся к так называемым неисправным элементам. Для моделирования предусмотрены три несправных элемента, соответствующих значению дозы уровней начального, среднего и конечного изменений параметров.

Эти уровни соответствуют следующим величинам дозы: начальной, когда изменения параметров только начинаются; конечной, при которой изменения выходят на норму технического задания или технических условий, и средней, расположенной в средней между ними точке.

Численные значения накопленной дозы высчитываются в зависимости от вида воздействия и его ионизационной составляющей. Другими словами, данный модуль позволяет свести всю сложную совокупность внешнего воздействия к понятиям дозы.

Комплекс программ расчета стойкости к электронному и протонному излучениям обеспечивает полное представление о стойкости изделия к факторам космического пространства.

Графический редактор обеспечивает ввод информации и вывод результатов расчета в наглядной форме. Программный модуль интерфейса пользователя предназначен для взаимодействия человека и ЭВМ.

Предусмотрена обучающая подсистема.

Литература

Ачкасов В.Н. Проектирование микроэлектронных компонентов космического назначения: монография. Воронеж: ВГУ, 2005. 270 с.