Software & Systems

Громоздкие выкладки при приближенном решении плоских задач нелинейной упругости и вязкоупругости аналитическими методами обусловливают необходимость автоматизировать аналитические вычисления. Специализированные системы, в которых реализованы алгоритмы, учитывающие особенности класса задач, для решения которых эти системы предназначены, позволяют эффективнее использовать ресурсы ЭВМ и за счет этого решать более сложные задачи.

Программный комплекс «Наложение» предназначен для решения плоских задач теории многократного наложения больших упругих и вязкоупругих деформаций для бесконечно протяженных тел с отверстиями различной формы и (или) круговыми включениями, возникающими последовательно или одновременно после предварительного нагружения [1, 2].

Задачи решаются методом малого параметра (методом последовательных приближений). Для задач образования одной полости или включения реализован метод Ньютона–Канторовича, применимый в более широком диапазоне деформаций. Линеаризованная задача для каждого приближения решается с использованием комплексных потенциалов Колосова–Мусхелишвили. При решении задач вязкоупругости применяется преобразование Лапласа. Для случая нескольких полостей и включений при решении линеаризованной задачи используется итерационный алгоритм Шварца. Результаты расчетов могут представляться как в аналитической форме, так и в числовой – в виде таблиц и графиков.

Постановка задач и методы их решения, реализованные в программном комплексе «Наложение», а также результаты расчетов подробно изложены в монографиях [1, 2]. Модифицированная версия программного комплекса, основанная на алгоритмах, представленных в [3–5], позволяет решать задачи для упругих и вязкоупругих тел, содержащих не только отверстия (в том числе и образованные после нагружения), но и жесткие включения, при конечных деформациях.

Аналитические преобразования реализованы в виде процедур-функций и объединены в модули для выполнения аналитических операций:

-    над изображениями по Лапласу (линейная комбинация изображений, умножение, свертка),

-    над функциями комплексных переменных специального вида (линейная комбинация функций, умножение, дифференцирование, интегрирование, подстановки специального вида); ориентирован на решение плоской задачи теории упругости методом Мусхелишвили, а также

-    для выполнения операций над тензорами второго ранга, компонентами которых являются функции комплексных переменных, используемые в предыдущем модуле (линейная комбинация тензоров, умножение, транспонирование, применение набла-оператора).

Основной программой является Windows-при­ложение, созданное в среде Delphi.

В качестве исходных данных задаются тип материала (механические свойства), геометрия включений и отверстий, нагрузки на бесконечности и величина сжатия (растяжения) включений. Комплекс позволяет приближенно решать задачи для тел из нелинейно-упругих сжимаемых и несжимаемых материалов (Мурнагана, Муни, Черных) и несжимаемого вязкоупругого материала специального класса [1, 2] в случаях плоской деформации и плосконапряженного состояния. Предусмотрена возможность расчета как для одновременного, так и для последовательного образования концентраторов напряжений. Результаты расчетов выводятся в текстовый файл. Также можно построить графики: эпюры напряжений, контуры концентраторов напряжений в деформированном состоянии, линии уровня.

При решении задач с помощью модифицированного программного комплекса «Наложение» можно исследовать зависимость напряженно-деформированного состояния от величины, вида и направления приложенной нагрузки, свойств материала, взаимного расположения концентраторов напряжения. Приведем примеры решения задач и результаты анализа, полученные с использованием программного комплекса.

Рассмотрим задачу о распределении напряжений в бесконечно протяженном нелинейно-упру­гом теле из материала Мурнагана с жестким круговым включением. Расчет выполнен для оргстекла: l=0,39´1012 дин/см2; G=0,186´1012 дин/см2; C3= –0,013´1012 дин/см2; C4= –0,07´1012 дин/см2; C5= 0,063´1012 дин/см2 [1]. Радиус включения – R, центр включения совпадает с началом координат.

На рисунке 1 приведена эпюра контурных истинных напряжений sjj/G на границе включения при одноосном сжатии на бесконечности s22/G= = –0,48. В правом верхнем углу приведена схема нагружения, в левом – масштаб напряжений, отнесенных к модулю сдвига G. Сплошная линия показывает линейное решение задачи, пунктирная – нелинейное, жирная сплошная линия – контур включения. Из рисунка 1 видно, что точка А и точка, симметричная ей относительно оси абсцисс, являются точками максимального по абсолютному значению напряжения для случая линейной задачи. Причем в случае решения задачи с учетом нелинейных эффектов напряжение в этих точках оказывается больше по абсолютному значению, чем в случае линейной задачи. С учетом нелинейной поправки в точке А и симметричной ей точке напряжение sjj/G увеличивается на 35 %. Для нелинейной задачи точками максимального положительного напряжения являются точки В, С и точки, симметричные им относительно начала координат. Значение напряжения в этих точках: sjj=0,10G. Численные значения взяты из соответствующего текстового файла.

Следующий расчет выполнен для бесконечно протяженного нелинейно-упругого тела с двумя жесткими круговыми включениями одинакового радиуса R. Центры включений находятся на оси ОХ. Расстояние между точками А и В, расположенными на оси ОХ, равно 0,8R (см. схему расположения включений на рисунке 2а). Расчет выполнен при одноосном растяжении в направлении оси ОХ . Материал тела несжимаемый (материал Муни).

На рисунке 2а приведена часть эпюры контурных истинных напряжений sjj/m на границе левого включения. В левом верхнем углу дан масштаб, напряжения отнесены к модулю сдви- га m. Для сравнения на рисунке 2б приведена часть эпюры контурных истинных напряжений sjj/m для случая одного включения. Видно, что наличие второго включения существенно влияет на истинное контурное напряжение.

Рассмотрим задачу об образовании треугольного отверстия в теле из вязкоупругого материала, содержащем жесткое включение круговой формы. Механические свойства исходного материала описаны в [1]. Расчеты выполнены при всестороннем растяжении на бесконечности (, остальные компоненты тензора истинных напряжений на бесконечности равны нулю) при значениях констант: A=0,0135–g, g=0,016, a=0,000167c–1, m=1 (полидиенэпоксиуретан); радиус включения – R. В декартовой системе координат центр отверстия – (0; 0), центр включения – (3,5; 0). Здесь и далее координаты приведены в долях R.

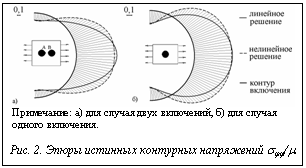
На рисунке 3 приведены эпюры истинных контурных напряжений: слева – эпюра контурных истинных напряжений sjj/m0 на границе отверстия, справа – на границе включения. На приведенной шкале указан масштаб напряжений, отнесенных к модулю сдвига m0. Решение приведено в момент t=12 с. Пунктирной линией обозначено решение задачи с учетом нелинейных эффектов. Особенно заметно их влияние на контуре отверстия. На рисунке также приведена схема расположения включения и отверстия относительно друг друга.

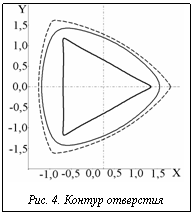
На рисунке 4 показана форма отверстия через 6 секунд после его образования. Треугольник внутри – намечаемая граница отверстия, два внешних контура – граница отверстия в указанный момент, сплошная линия соответствует линейному решению задачи, пунктирная – решению задачи с учетом нелинейных эффектов. На рисунке видно заметное влияние нелинейных эффектов на форму контура.

С помощью рассмотренного программного комплекса можно решать прикладные задачи по выполнению прочностных расчетов и анализу возможности разрушения элементов конструкций. Например, программный комплекс может использоваться при расчете на прочность резинокордных композитов при образовании в них дефектов различной формы, а также как средство тестирования для численного решения задач, например, методом конечных элементов.

Литература

1.   Левин В.А., Зингерман К.М. Плоские задачи теории многократного наложения больших деформаций. Методы решения. М.: Наука, 2002. 272 c.

2.   Левин В.А. [и др.]. Развитие дефектов при конечных деформациях. Компьютерное и физическое моделирование. М.: Физматлит, 2007. 392 с.

3.   Рябова О.А., Зингерман К.М. Численно-аналитическое моделирование напряженно-деформированного состояния вблизи жестких включений в теле из нелинейно-упругого материала с учетом их взаимовлияния // Вест. Тверского гос. ун-та: сер. Прикладная математика. Тверь: Изд-во ТГУ. 2007. № 27 (55). С. 89–98.

4.   Рябова О.А., Зингерман К.М. Нелинейная модель образования жестких включений в бесконечно протяженном упругом теле и методы ее исследования // Там же. 2009. № 28. С. 37–44.

5.   Зингерман К.М., Рябова О.А. Взаимовлияние полости и жесткого включения в нелинейно-упругом теле при конечных деформациях // Изв. ТулГУ: Естественные науки. Тула, 2010. Вып. 2. С. 64–72.