Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: () - , () - | |
| Page views: 12690 |
Print version Full issue in PDF (2.00Mb) |
Для решения задачи многокритериальной оптимизации в настоящее время все более широкое распространение находят методы, основанные на принципе «гибкого приоритета». Принцип «гибкого приоритета» в общем случае сводится к дополнительному нормированию показателей качества, что позволяет в разумных приделах учесть степень предпочтения одного показателя перед другим. При этом предполагается, что влияние каждого i-го единичного показателя на величину функции предпочтения зависит не только от нормированного значения этого показателя, но и от некоторого весового коэффициента В настоящее время известен ряд самых различных функций предпочтения, учитывающих принцип гибкого приоритета, среди которых более широкое распространение получили линейные аддитивные функции предпочтения. В работе предлагаются нелинейные неаддитивные функции предпочтения, обладающие большой потенциальной адекватностью, что позволяет учесть нелинейность зависимости функций предпочтения от нормированных значений показателей и разброс этих значений. Рассмотрим определение аддитивных, но нелинейных функций предпочтения. Учитывая коэффициенты важности отдельных показателей, выражение для полиномиальной функции предпочтения примет вид:
где Y – значение полиномиальной функции предпочтения; При этом предполагается, что весовые коэффициенты также пронормированы, то есть Под условными функциями предпочтения понимается функция предпочтения по i-му показателю, полученному при условии, что значения остальных показателей соответствуют середине диапазона их изменения. Будем считать, что все нормированные показатели качества являются однородными, то есть имеют одну общую интервальную шкалу, пределы которой меняются от 0 до +1. Тогда в работе для определения условных нелинейных функций предпочтения предлагается использовать преобразованную психофизическую шкалу Фехнера, которую можно представить в виде:
где С увеличением Наиболее сложной задачей, возникающей при многокритериальной оптимизации, является определение неаддитивной функции предпочтения, учитывающей разброс нормированных значений показателей. Так как показатели качества являются однородными, то их значениям соответствуют множество точек этой шкалы. С учетом значений высоких коэффициентов
Средневзвешенное расстояние позволяет учесть важность каждого показателя при оценке нежелательности их разброса. Пронормируем величину средневзвешенного расстояния d. С этой целью введем максимальное внутримножественное расстояние для n показателей. При этом максимальному значению соответствует случай, когда все показатели принимают граничные значения, а весовые коэффициенты С учетом вышесказанного неаддитивную функцию предпочтения можно представить в виде:
где На основе выражений неаддитивной и условной функции предпочтения (2) и (4) и внутримножественного расстояния (3) может быть осуществлен выбор оптимальных решений в многокритериальных задачах оптимизации. |
| Permanent link: http://swsys.ru/index.php?id=302&lang=en&page=article |
Print version Full issue in PDF (2.00Mb) |
| The article was published in issue no. № 4, 2007 |
Back to the list of articles
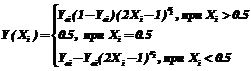 , (2)
, (2)