Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: () - , () - | |
| Page views: 12528 |
Print version Full issue in PDF (2.00Mb) |
Ошибки системы управления (СУ), определяющие отклонение точки падения от точки прицеливания, приближенно можно выразить следующими формулами:
где Ошибки Для выбора алгоритма корреляционно экстремальной обработки (КЭО), его параметров, логики измерений и профиля траектории необходимо определить критерий эффективности, позволяющий сравнивать альтернативные варианты. Критерий эффективности – это скалярная количественная мера степени соответствия системы ее назначению. Назначением системы является поражение объекта или его жизненно важных точек, поэтому общим критерием эффективности является вероятность поражения. Если аппроксимировать координатный закон поражения симметричной гауссоидой:
где
Точность СУ обычно характеризуется одним числом вида:
Если в (3) положить Как указывалось выше, эффективность СУ без коррекции можно характеризовать выражениями (1), (3), (4). При этом в (1) a и g полагаются равными нулю, а в ошибках Работа системы коррекции сводится к оценке ошибок ПИУ по измерениям геофизического поля (ГФП). В общем случае вектор оцениваемых параметров ПИУ имеет вид:
где Идеальная система коррекции должна оценивать весь вектор состояния ПИУ по измерениям ГФП, а также ошибки привязки лучей радиолокатора рельефометрической системы (РРС) к осям ПИУ. Для реальных систем состав оцениваемых параметров ПИУ определяется на начальном этапе проектирования в зависимости от их вклада в общий баланс ошибок (1) и является важнейшей частью задачи выбора или разработки алгоритма КЭО и облика КЭНС. Точность СУ с коррекцией по ГФП, заданная выражением (4), определяющим образом зависит от высоты и длины участка коррекции. Для баллистического аппарата, движущегося в атмосфере, высота и длина участка коррекции – взаимосвязанные параметры: с уменьшением высоты уменьшается и длина участка коррекции. Поскольку при этом увеличивается разрешение РРС, то существует оптимальная высота участка, при которой ошибка СУ (4) становится минимальной. Важна и точность выхода на заданную высоту в начале участка коррекции. Можно сказать, что точность СУ (4) повышается прямо пропорционально объему информации, содержащемуся в массиве измерений РРС. Этот объем главным образом зависит от длины участка коррекции и разрешения РРС, определяемого диаметром пятна засветки. Число лучей РРС влияет на объем информации только в том случае, если расстояние между центрами пятен засветки боковых лучей больше радиуса корреляции рельефа, сглаженного пятном засветки. Однако при увеличении угла раствора крайних боковых лучей уменьшается разрешение в боковом направлении и увеличивается флуктуационная ошибка РРС и ошибка смещения. Поэтому он ограничен величиной 10-12 градусов. Вероятно, разрешение РРС в боковом направлении можно улучшить, если использовать не всю ширину отраженного сигнала, а только его центральную часть. Но это требует проведения оценочных расчетов. Поскольку точность выхода в начало участка коррекции по высоте имеет большое значение, в том числе и как фактор, увеличивающий длину участка, то в логику измерений целесообразно ввести участок предварительного измерения высоты еще в достаточно плотной плазме. В этом случае момент включения РРС на излучение необходимо формировать по достижении заданной скорости. Для максимального использования потенциала РРС на этом участке передатчик должен работать на один центральный луч, а количество накапливаемых в процессе обработки импульсов необходимо увеличить. Этот дополнительный участок позволит существенно повысить точность выхода по высоте на начало основного участка. Кроме того, эти дополнительные измерения можно использовать для повышения точности коррекции на основном участке, если их ввести в решающую функцию с соответствующими весами, вид которых уточняется в дальнейшем:
где k – номер измерения (дискретное время); m – номер луча; После основного участка коррекции РРС можно также не отключать и работать на один центральный луч и на участке пикирования. Если на конечном участке летательный аппарат (ЛА) интенсивно маневрирует по крену, то используются измерения луча, который ближе всех к вертикали. Эти дополнительные измерения, как и на предварительном участке, возможно, позволят повысить конечную точность как за счет увеличения объема информации, так и за счет уменьшения оставшегося времени Таким образом, в логику измерений целесообразно ввести три участка и с учетом этого выбрать оптимальный профиль траектории, то есть высоту начала участка коррекции, его длину и угол наклона траектории. В конечную точность (4) вносит свой вклад не только алгоритм КЭО, но и профиль траектории, логика измерений и способ обработки сигнала РРС. Поэтому необходим системный подход к выбору облика системы коррекции и ее параметров. Выбор облика системы должен начинаться с анализа общего баланса ошибок (1) и чувствительности каждой составляющей к тому или иному техническому решению. Идеальным средством для такого системного проектирования является имитационная математическая модель системы коррекции, в которую входит подробная модель РРС, модель ГФП, бесплатформенной инерциальной навигационной системы (БИНС) и модель движения ЛА. Испытания на летающей лаборатории используются для подтверждения правильности принятых технических решений и идентификации некоторых трудно формализуемых параметров математической модели. Степень совпадения точности системы коррекции, полученной на летных испытаниях, с данными математической модели является критерием ее адекватности. Рельефометрическая КЭНС работает на основе сравнения измеренного профиля рельефа с эталонными профилями, вычисляемыми по эталонной карте местности (ЭКМ). Измеренная высота рельефа и координаты точки пересечения осей ДНА с земной поверхностью по данным БИНС в k-й момент времени для середины временного интервала накопления отраженных импульсов вычисляются по формулам:
где Относительно точки Предполагается, что ошибка ИНС по высоте частично скомпенсирована на предварительном участке коррекции, и поэтому гипотезы по высоте не строятся. Для каждой гипотезы в узлах сетки вычисляется эталонная высота
где N – количество измерений; mm – число лучей; k – номер текущего измерения (дискретное время); i,j – номера узлов гипотезной сетки; im, jm – размер гипотезной сетки; Здесь среднее значение – это линейный тренд измеренного профиля. Коэффициенты При такой записи решающей функции предполагается, что линейный тренд выделен и в ЭКМ, в противном случае линейный тренд выделяется из разности измеренного и эталонного профилей. В таком представлении измеренный и эталонный профили рельефа рассматриваются как центрированные псевдослучайные процессы. Для истинного местоположения решающая функция (8) принимает минимальное значение. Поскольку истинное значение минимума находится между узлами гипотезной сетки, то в окрестности минимальной гипотезы решающая функция аппроксимируется поверхностью второго порядка методом наименьших квадратов и точка ее минимума принимается за оценку местоположения. Можно также в окрестности минимальной гипотезы вычислять центр тяжести решающей функции. Процедура уточнения координат по центру тяжести, известная как алгоритм центроиды, широко применяется в оптических системах обнаружения и измерения координат точечных объектов. Поправки к показаниям ИНС
Рассмотренный базовый алгоритм очень близок к классическому корреляционному алгоритму с центрированием и нормированием. |
| Permanent link: http://swsys.ru/index.php?id=307&lang=en&page=article |
Print version Full issue in PDF (2.00Mb) |
| The article was published in issue no. № 4, 2007 |
Back to the list of articles
 . (3)
. (3)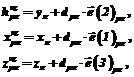 (7)
(7) , (8)
, (8)