Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: () - , () - | |
| Page views: 13248 |
Print version Full issue in PDF (2.00Mb) |
Обоснованность результатов применения классических методов оценки инвестиционных проектов (ИП) в условиях стохастической неопределенности и базирующихся на них систем поддержки принятия инвестиционных решений (СППИР) обусловлена жесткими предположениями относительно характеристик ИП, объема и свойств исходных данных, а также предпочтений ЛПР. Указанные предположения, как правило, не соответствуют реальности. Поэтому разработка методов оценки ИП, не критичных к нарушению допущений классических подходов, а также совершенствование на их основе СППИР является актуальной задачей. В данной работе представляются компоненты СППИР, которая включает в себя пользовательский интерфейс, базу методов расчета остаточной стоимости (капитализации) проекта, базу статистических данных и некритичные к допущениям классических методов функциональные модули, предназначенные для решения следующих задач: восстановления функции полезности (ФП) ЛПР; выбора проектов с позиций капитализации; выбора проектов с позиций обеспечиваемого дохода; поиска оптимального инвестиционного портфеля; осуществления имитационного моделирования. Восстановление ФП ЛПР. Модуль осуществляет структурную и параметрическую идентификацию одно- и двухкритериальных ФП. Восстановление ФП на критерии y осуществляется с использованием интервальных оценок предпочтений ЛПР, которые представляются областями
где Двухкритериальная ФП Задача выбора проектов с позиций капитализации. Данный модуль обеспечивает выбор ИП из множества Динамика капитализации каждого проекта представляется случайным процессом
здесь Остаточная стоимость оценивается с использованием известных методов. Величина Задача выбора проектов с позиций обеспечиваемой доходности. Модуль осуществляет выбор проектов при стремлении ЛПР к максимальной обеспечиваемой доходности. На вход модуля подается информация о желаемом для ЛПР уровне Задача выбора с учетом динамики капитализации формализуется в следующем виде:
здесь Задача поиска оптимальных инвестиционных портфелей. Модуль решает задачу распределения капитала между проектами из J:
здесь Для нахождения Имитационное моделирование. Для решения вышеописанных задач в условиях отсутствия информации о распределениях
где В заключение отметим, что представленная СППИР обладает следующими достоинствами: позволяет работать с проектами инвестиций в материальные активы, учитывает многопериодные аспекты реализации проектов, в целом более адекватно отражает реальные условия. |
| Permanent link: http://swsys.ru/index.php?id=314&lang=en&page=article |
Print version Full issue in PDF (2.00Mb) |
| The article was published in issue no. № 4, 2007 |
Back to the list of articles
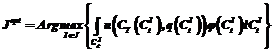 ,
,