В современных многопроцессорных вычислительных системах (МВС) время выполнения параллельной программы может существенно зависеть от того, как ее отдельные ветви размещены по вычислительным узлам (ВУ) и процессорам [1]. Значительное влияние на время выполнения параллельной программы оказывает конкуренция между взаимодействующими ветвями за коммуникационный ресурс или память ВУ [2]. В качестве примера можно рассмотреть схемы размещения ветвей параллельных программ CG (рис. 1а) и SP (рис. 1б) из тестового пакета NAS Parallel Benchmarks [3] на процессорах ВУ, при которых через коммутатор выполняется 8 одновременных пересылок. Увеличение числа конкурирующих пересылок через коммутатор приводит к значительному увеличению времени выполнения программ CG (рис. 2а) и SP (рис. 2б). В работе [2] отмечается, что конкуренция между ветвями параллельной программы приводит к увеличению латентности и уменьшению пропускной способности коммуникационной среды МВС.
Анализ программ, выполняемых на програм- мно-техническом комплексе Санкт-Петербургского государственного политехнического университета (ПТК СПГПУ) и вычислительных ресурсах Межведомственного суперкомпьютерного центра Российской академии наук (МСЦ РАН), показал, что в параллельных алгоритмах используются стандартные схемы коммуникационных обменов (коммуникационные шаблоны). Под коммуникационным шаблоном будем понимать схему обмена данными между параллельными ветвями программы заданного этапа алгоритма. Как правило, параллельная программа использует фиксированный набор коммуникационных шаблонов, которые повторяются в процессе ее выполнения. Учет коммуникационных шаблонов при распределении ветвей параллельной программы по процессорам МВС позволяет выявлять конкуренцию за коммуникационные ресурсы на различных этапах выполнения программы.
Для формализации оптимизационной задачи по минимизации времени выполнения параллельного приложения построим математические модели параллельной программы и МВС.
Модель параллельной программы
Коммуникационный шаблон может быть представлен в виде графа I=(V, E), вершины V которого соответствуют ветвям программы, а ребра E представляют информационные связи между ними. На множестве V зададим отображения:
 , где T соответствует различным типам вычислительных устройств, а функция
, где T соответствует различным типам вычислительных устройств, а функция  ставит в соответствие вершине vi графа I тип вычислительного устройства, на котором может быть запущена ветвь с номером i;
ставит в соответствие вершине vi графа I тип вычислительного устройства, на котором может быть запущена ветвь с номером i;
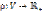 ; функция p(vi) ставит в соответствие вершине vi графа I количество вычислительных операций, выполненных ветвью с номером i.
; функция p(vi) ставит в соответствие вершине vi графа I количество вычислительных операций, выполненных ветвью с номером i.
На множестве ребер E заданы отображения:

 ставит в соответствие ребру eij графа
ставит в соответствие ребру eij графа 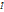 объем данных, переданный между ветвями с номерами i и j за время выполнения коммуникационного шаблона;
объем данных, переданный между ветвями с номерами i и j за время выполнения коммуникационного шаблона;
 ставит в соответствие ребру eij графа I число операций приема/передачи данных между ветвями с номерами i и j за время выполнения параллельной программы.
ставит в соответствие ребру eij графа I число операций приема/передачи данных между ветвями с номерами i и j за время выполнения параллельной программы.
Параллельная программа, использующая s отличных друг от друга коммуникационных шаблонов, может быть представлена в виде объединения графов:
I=I1ÈI2È … ÈIs=(V1ÈV2È … ÈVs;
E1ÈE2È … ÈEs). (1)
Каждый шаблон  параллельной программы может быть описан с помощью матрицы смежности
параллельной программы может быть описан с помощью матрицы смежности 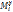 . Элемент eij матрицы
. Элемент eij матрицы 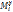 соответствует ребру графа программы, отражающему информационную связь между ветвями vi и vj. Если eij=0, то в коммуникационном шаблоне Is ветви vi и vj не взаимодействуют друг с другом. Приведем пример матрицы
соответствует ребру графа программы, отражающему информационную связь между ветвями vi и vj. Если eij=0, то в коммуникационном шаблоне Is ветви vi и vj не взаимодействуют друг с другом. Приведем пример матрицы 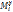 для коммуникационного шаблона «кольцо» информационного графа программы:
для коммуникационного шаблона «кольцо» информационного графа программы:
| |
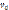
|

|
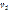
|

|
…
|

|

|

|
|
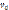
|
0
|

|
0
|
0
|
0
|
0
|

|
|

|

|
0
|

|
0
|
0
|
0
|
0
|
|
|
0
|

|
0
|

|
0
|
0
|
0
|
|

|
0
|
0
|

|
0
|
0
|
0
|
0
|
|
…
|
|

|
0
|
0
|
0
|
0
|
…
|
0
|

|
0
|
|

|
0
|
0
|
0
|
0
|

|
0
|

|
|

|

|
0
|
0
|
0
|
0
|

|
0
|
На рисунке 3 представлены коммуникационные шаблоны тестов NAS Parallel Benchmarks BT и CG в виде матриц смежности. Номера строк и столбцов матриц соответствуют номерам MPI-процессов, а закрашенные элементы матриц показывают наличие или отсутствие коммуникационного обмена между этими процессами.
Для автоматизации процесса построения информационного графа и выделения коммуникационных шаблонов использовалось программное средство IGtrace [1].
Модель многопроцессорной вычислительной системы
 Структура МВС может быть представлена в виде дерева, содержащего M уровней. Каждый уровень образован отдельным видом вычислительных компонентов МВС (телекоммуникационные шкафы, вычислительные узлы и др.), которые объединены линиями связи своего уровня. Для каждого узла дерева определен граф ВС, отражающий структуру коммуникационной среды дочерних элементов следующего уровня. Обозначим
Структура МВС может быть представлена в виде дерева, содержащего M уровней. Каждый уровень образован отдельным видом вычислительных компонентов МВС (телекоммуникационные шкафы, вычислительные узлы и др.), которые объединены линиями связи своего уровня. Для каждого узла дерева определен граф ВС, отражающий структуру коммуникационной среды дочерних элементов следующего уровня. Обозначим  граф ВС с номером j на уровне иерархии i (рис. 4а).
граф ВС с номером j на уровне иерархии i (рис. 4а).
На рисунке 4б приведен пример графа МВС, который отражает три уровня иерархии коммуникационной среды и включает несколько типов вычислительных устройств  . В качестве вычислительного устройства типа T1 может выступать универсальный процессор, а вычислительного устройства типа T2 – графический процессор. МВС состоит из двух ВУ, каждый из которых содержит от двух до четырех многоядерных процессоров. Первый уровень
. В качестве вычислительного устройства типа T1 может выступать универсальный процессор, а вычислительного устройства типа T2 – графический процессор. МВС состоит из двух ВУ, каждый из которых содержит от двух до четырех многоядерных процессоров. Первый уровень 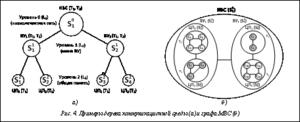 коммуникационной среды, представленный графом
коммуникационной среды, представленный графом  , образован низколатентной сетью (например InfiniBand), через которую взаимодействуют ВУ. На втором уровне иерархии, представленном графами
, образован низколатентной сетью (например InfiniBand), через которую взаимодействуют ВУ. На втором уровне иерархии, представленном графами  и
и  , для выполнения обменных операций между процессорами (ЦП) используется шина. Третий уровень образован вычислительными ядрами процессоров и представлен графами
, для выполнения обменных операций между процессорами (ЦП) используется шина. Третий уровень образован вычислительными ядрами процессоров и представлен графами  . Обмен данными между ядрами процессоров осуществляется через общую память.
. Обмен данными между ядрами процессоров осуществляется через общую память.
Приведенный на рисунке 4б граф МВС может быть представлен в виде следующей матрицы смежности  :
:
Элемент  матрицы
матрицы  соответствует ребру графа ВС, соединяющему вычислительные устройства ci и cj на уровне иерархии k. Если элемент
соответствует ребру графа ВС, соединяющему вычислительные устройства ci и cj на уровне иерархии k. Если элемент  , значит, прямой линии связи между вычислительными элементами ci и cj не существует.
, значит, прямой линии связи между вычислительными элементами ci и cj не существует.
На множестве вершин  графа
графа  зададим отображения:
зададим отображения:
 , где T соответствует различным типам вычислительных устройств, а функция
, где T соответствует различным типам вычислительных устройств, а функция  ставит в соответствие вершине
ставит в соответствие вершине  тип
тип  вычислительного ядра p;
вычислительного ядра p;
 ; функция
; функция  ставит в соответствие вершине
ставит в соответствие вершине  производительность вычислительного ядра p.
производительность вычислительного ядра p.
Ребра  – это линии связи, соединяющие между собой элементы графа
– это линии связи, соединяющие между собой элементы графа  , то есть
, то есть  где
где  . На множестве ребер Lk заданы отображения:
. На множестве ребер Lk заданы отображения:
 ; функция
; функция  ставит в соответствие ребру
ставит в соответствие ребру  значение пропускной способности линии связи между вычислительными элементами с номерами i и j на уровне k;
значение пропускной способности линии связи между вычислительными элементами с номерами i и j на уровне k;
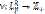 ; функция
; функция  ставит в соответствие ребру
ставит в соответствие ребру  значение латентности линии связи между вычислительными элементами с номерами i и j на уровне k.
значение латентности линии связи между вычислительными элементами с номерами i и j на уровне k.
Для автоматизации процесса построения матрицы Ms могут использоваться программные средства из [4]. С помощью тестовой программы необходимо измерить латентность и пропускную способность сети между каждой парой вычислительных устройств и воспользоваться программой визуализации для выделения уровней иерархии коммуникационной среды на основе полученных результатов тестирования [4].
Задача эффективного размещения программ на ресурсах МВС
Пусть задан граф вычислительной системы S=(C, L), содержащий k различных типов вычислительных устройств. На множестве вершин C графа ВС заданы отображения  ,
,  и
и  . На множестве ребер
. На множестве ребер  заданы отображения
заданы отображения 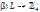 и
и  .
.
Информационный граф I=(V, E) параллельной программы, состоящей из s коммуникационных шаблонов, представлен набором графов  , для которых выполняется условие (1). На множестве вершин V заданы отображения
, для которых выполняется условие (1). На множестве вершин V заданы отображения 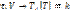 ,
,  и
и 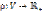 . На множестве ребер E заданы отображения
. На множестве ребер E заданы отображения  и
и  .
.
Отображение информационного графа параллельной программы I=(V, E) на структуру вычислительной системы, заданной графом S=(C, L), обозначается как 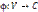 и представляется матрицей
и представляется матрицей 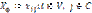 , где
, где 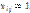 , если
, если  , и
, и  , если
, если 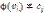 .
.
Время выполнения параллельной программы (Tp) включает в себя время выполнения вычислительных операций наиболее длительной ветви программы (Tcalc), время выполнения коммуникационных обменов (Tcomm) между ветвями программы и время, затраченное на синхронизацию ветвей программы (Tsync). Таким образом, время выполнения параллельной программы можно представить в виде суммы:
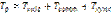 . (2)
. (2)
Для уменьшения значения Tp необходимо уменьшить значения слагаемых (2). Значение Tsync в большей степени зависит от того, как реализован алгоритм программы, поэтому в дальнейшем его можно не учитывать и принять за константу Tsync= =const. Значение Tcalc может быть уменьшено путем размещения ветвей программы на более производительных вычислительных устройствах. Время выполнения обменных операций Tcomm между ветвями программы зависит от характеристик коммуникационного оборудования и памяти ВС.
С учетом введенных обозначений задача размещения программы на вычислительных ресурсах многопроцессорной вычислительной системы может быть сформулирована следующим образом. Требуется найти такое отображение  , при котором
, при котором
 . (3)
. (3)
Время  выполнения
выполнения  вычислительных операций типа
вычислительных операций типа  ветвью
ветвью 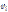 программы на вычислительном устройстве
программы на вычислительном устройстве  типа
типа  с производительностью
с производительностью  можно определить следующим образом:
можно определить следующим образом:
 (4)
(4)
Тогда время выполнения вычислительных операций наиболее длительной ветви параллельной программы на наборе вычислительных устройств может быть определено как
 (5)
(5)
Пусть вершины  информационного графа программы отображены на вершины
информационного графа программы отображены на вершины  графа ВС соответственно. Обозначим Lmn множество ребер, формирующих кратчайший путь от вершины cm к вершине cn. Тогда время выполнения обменных операций
графа ВС соответственно. Обозначим Lmn множество ребер, формирующих кратчайший путь от вершины cm к вершине cn. Тогда время выполнения обменных операций  между ветвями vi и vj можно вычислить по формуле
между ветвями vi и vj можно вычислить по формуле
 . (6)
. (6)
Время 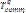 выполнения коммуникационного шаблона
выполнения коммуникационного шаблона  с графом
с графом  равно максимальной по длительности операции приема/передачи из данного шаблона:
равно максимальной по длительности операции приема/передачи из данного шаблона:

 (7)
(7)
Поскольку коммуникационные шаблоны выполняются последовательно, время Tcomm выполнения всех коммуникационных операций можно вычислить следующим образом:
 (8)
(8)
Подставляя (5) и (8) в (3), получим:

 (9)
(9)

Алгоритмы размещения параллельных программ на ресурсах МВС
В современных системах управления вычислительными ресурсами и заданиями (СУРЗ), к числу которых можно отнести СУППЗ, Slurm, Cleo и Torque, параллельная программа пользователя рассматривается как совокупность независимо выполняемых ветвей. Каждая ветвь программы распределяется на отдельный процессор или вычислительное ядро в соответствии с одним из реализуемых СУРЗ алгоритмов планирования:
PAL (Processor Allocation Linear) – осуществляется выбор первых M свободных процессоров (вычислительных ядер);
PAR (Processor Allocation Random) – случайным образом выбирает M процессоров (вычислительных ядер) из числа свободных;
TMRR (Task Map Round Robin) – распределяет ветви программы по процессорам системы из N вычислительных узлов в следующем порядке: первая ветвь программы размещается на первом процессоре первого по порядку выделенного заданию вычислительного узла (ВУ), вторая – на первом процессоре второго ВУ, ветвь N – на первом процессоре ВУ N, ветвь N+1 – на втором процессоре первого ВУ и т.д.
Перечисленные алгоритмы не учитывают неоднородность вычислительной и коммуникационной инфраструктур МВС, а также порядок взаимодействия между ветвями и интенсивность выполнения обменных операций.
Задача эффективного размещения ветвей параллельной программы на процессорах МВС является NP-полной. Для ее решения сегодня существует несколько классов алгоритмов. Часть этих алгоритмов являются эвристическими, то есть дающими лишь приближенное решение задачи, часть – точными. В работе [5] отмечается целесообразность применения точных алгоритмов только для систем с малым числом процессоров, не превышающим 10. Обзор существующих эвристических алгоритмов размещения параллельных программ показал, что наиболее предпочтительными по точности получаемого результата являются алгоритмы, основанные на методе моделирования отжига (алгоритмы имитации отжига).
В общем виде алгоритм имитации отжига для решения задачи отображения информационного графа программы на граф ВС, заданных матрицами MI и MS соответственно, можно описать следующим образом.
Шаг 1. Установить начальную температуру  и значение счетчика итераций t равным 0.
и значение счетчика итераций t равным 0.
Шаг 2. Выбрать начальное произвольное отображение Xj (алгоритмом PAL или PAR) и вычислить значение F(Xj) функционала (9).
Шаг 3. Выбрать произвольную вершину vi информационного графа.
Шаг 4. Поместить вершину vi на вершину cj графа ВС. Вычислить новое значение 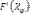 функционала (9).
функционала (9).
Шаг 5. Вычислить приращение функционала  . Если
. Если 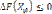 , вершина vi закрепляется за вершиной cj. Если
, вершина vi закрепляется за вершиной cj. Если  , закрепление вершины vi за вершиной cj осуществляется с вероятностью
, закрепление вершины vi за вершиной cj осуществляется с вероятностью  .
.
Шаг 6. Если все вершины cj были пройдены, понизить температуру T по закону 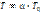 , где
, где  – параметр, влияющий на скорость понижения температуры, и перейти к шагу 3. Если зафиксирован выход функционала
– параметр, влияющий на скорость понижения температуры, и перейти к шагу 3. Если зафиксирован выход функционала  на стационарное значение или текущее значение T является конечным, завершить работу алгоритма. В остальных случаях увеличить значение j на 1 и перейти к шагу 4.
на стационарное значение или текущее значение T является конечным, завершить работу алгоритма. В остальных случаях увеличить значение j на 1 и перейти к шагу 4.
Обозначим как 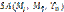 приведенный алгоритм отображения вершин информационного графа I на вершины графа ВС S с заданными начальной и конечной температурами соответственно.
приведенный алгоритм отображения вершин информационного графа I на вершины графа ВС S с заданными начальной и конечной температурами соответственно.
Эффективность (время выполнения и точность) алгоритма 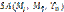 зависит от начальной температуры T0, предельного числа итераций (значение параметра
зависит от начальной температуры T0, предельного числа итераций (значение параметра  ), размера области сходимости (числа последовательных итераций, в течение которых значение функционала остается неизменным). При увеличении указанных параметров возрастают точность и время выполнения алгоритма.
), размера области сходимости (числа последовательных итераций, в течение которых значение функционала остается неизменным). При увеличении указанных параметров возрастают точность и время выполнения алгоритма.
Параллельная реализация алгоритма имитации отжига
Одним из подходов к уменьшению времени работы алгоритма 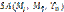 является его распараллеливание. В настоящее время известно несколько способов распараллеливания алгоритма имитации отжига.
является его распараллеливание. В настоящее время известно несколько способов распараллеливания алгоритма имитации отжига.
1. Параллельный независимый запуск алгоритма имитации отжига на нескольких узлах с различными начальными приближениями. В качестве результата выбирается лучшее решение из найденных на всех узлах. Скорость поиска решений и их качество практически не отличаются от классического последовательного алгоритма.
2. Параллельный запуск алгоритма имитации отжига с периодическим обменом информацией о полученных решениях, при этом узлы вычислительной системы производят рестарт имитации отжига из найденных решений с наименьшим значением целевой функции. Такой способ универсален и приемлем для любых задач оптимизации, но требует больших затрат на обмен данными.
3. Разбиение пространства решений на области и поиск решения в каждой области отдельно с последующим объединением результатов поиска и выбором из них лучшего решения. Такой способ может эффективно применяться на широком классе архитектур, но требует разработки способа разбиения на области для каждой решаемой задачи.
 Первые два способа распараллеливания алгоритма имитации отжига предполагают, что на каждом из вычислительных узлов доступна своя копия графа ВС и информационного графа программы. Данное условие может затруднять реализацию предложенных подходов для графов параллельной программы и ВС, которые невозможно целиком разместить в памяти одного ВУ. Поэтому для распараллеливания алгоритма имитации отжига был выбран способ, основанный на разбиении пространства поиска решений на независимые области.
Первые два способа распараллеливания алгоритма имитации отжига предполагают, что на каждом из вычислительных узлов доступна своя копия графа ВС и информационного графа программы. Данное условие может затруднять реализацию предложенных подходов для графов параллельной программы и ВС, которые невозможно целиком разместить в памяти одного ВУ. Поэтому для распараллеливания алгоритма имитации отжига был выбран способ, основанный на разбиении пространства поиска решений на независимые области.
Обозначим  матрицу смежности информационного графа программы размера
матрицу смежности информационного графа программы размера  , а
, а  – матрицу смежности графа ВС размера
– матрицу смежности графа ВС размера 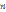 , где
, где  . Выполним декомпозицию графа ВС по ВУ путем разбиения матрицы
. Выполним декомпозицию графа ВС по ВУ путем разбиения матрицы  на k частей. Обозначим
на k частей. Обозначим  , часть матрицы
, часть матрицы  , размещенную в памяти i-го ВУ.
, размещенную в памяти i-го ВУ.
Параллельная реализация алгоритма имитации отжига  для k ВУ может быть описана следующим образом.
для k ВУ может быть описана следующим образом.
Шаг 1. Выполнить в цикле.
Шаг 1.1. Сформировать новое допустимое сочетание  элементов матрицы смежности графа ВС
элементов матрицы смежности графа ВС  . Допустимым является сочетание, соответствующее назначению ветви параллельной программы на один процессор или вычислительное ядро.
. Допустимым является сочетание, соответствующее назначению ветви параллельной программы на один процессор или вычислительное ядро.
Шаг 1.2. Передать значения элементов  очередному ВУ i в качестве элементов матрицы
очередному ВУ i в качестве элементов матрицы  для выполнения алгоритма моделирования отжига.
для выполнения алгоритма моделирования отжига.
Шаг 1.3. На каждом процессоре i-го ВУ выполнить алгоритм имитации отжига 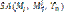 .
.
Шаг 1.4. Для каждого ВУ выбрать лучшее решение из найденных на всех процессорах.
Шаг 1.5. Выбрать лучшее решение из найденных на всех ВУ.
Шаг 2. Если все сочетания рассмотрены, завершить выполнение алгоритма и принять в качестве искомого лучшее из найденных в процессе выполнения алгоритма решение. Иначе перейти на шаг 1 алгоритма.
Экспериментальные результаты
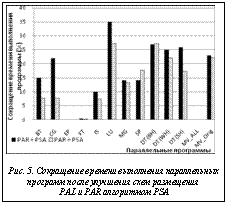
Для оценки эффективности разработанного алгоритма было выполнено размещение параллельных программ из тестового пакета NAS Parallel Benchmarks на ресурсах МВС с сетевой топологией «двумерная решетка» и состоящей из 64 процессоров. Запуск тестов осуществлялся на 8, 16, 32 и 64 процессорах. Для каждого теста с помощью функционала (9) вычислялось время выполнения коммуникационных обменов между ветвями после их размещения на процессорах с помощью алгоритмов PAL и PAR. Полученные схемы размещений улучшались с помощью разработанного алгоритма PSA, и вычислялось текущее время выполнения коммуникационных обменов. На рисунке 5 представлена диаграмма изменения времени выполнения тестов NAS Parallel Benchmarks и двух реализаций параллельного алгоритма умножения разреженной матрицы на вектор (MV_ALL и MV_Orig) после улучшения схем размещения PAL (PAL+PSA) и PAR (PAR+PSA). Среднее время построения новой схемы размещения ветвей на процессорах МВС с помощью алгоритма PSA не превышало 10 % от времени выполнения тестовой программы.
Как видно из рисунка 5, для двух тестов NAS Parallel Benchmarks (EP и FT) и программы MV_ALL не удалось уменьшить время выполнения. Это объясняется тем, что в первых двух программах объем вычислений преобладает над количеством коммуникационных операций, а в третьей реализован обмен каждый-с-каждым. Для остальных программ время выполнения удалось сократить от 10 до 43 %.
Предложенный алгоритм отображения графа программы на граф ВС был реализован на языке С++ в виде программного модуля, который в дальнейшем может быть интегрирован в СУРЗ МВС. Запуск алгоритма осуществлялся с использованием программного комплекса «Пирамида» [6] на вычислительных ресурсах ПТК СПГПУ и МСЦ РАН.
В заключение отметим следующее. В МВС время выполнения параллельной программы зависит от того, как ее отдельные ветви размещены по вычислительным узлам и процессорам. Значительное влияние на время выполнения параллельной программы, а также латентность и пропускную способность коммуникационной среды оказывает конкуренция между взаимодействующими ветвями за коммуникационный ресурс.
Для уменьшения времени выполнения параллельной программы и сокращения конкуренции в сети предложен подход, основанный на выявлении и учете типовых коммуникационных операций в программе (коммуникационных шаблонов) при ее размещении на ресурсах МВС. Разработан параллельный алгоритм размещения программ на ресурсах МВС, основанный на методе моделирования отжига.
Результаты проведенных экспериментов показали существенное сокращение времени выполнения параллельных программ и целесообразность применения разработанного подхода и алгоритма для решения задачи эффективного размещения параллельной программы на ресурсах МВС. Программная реализация предложенного алгоритма размещения ветвей параллельной программы на вычислительных ресурсах МВС может быть интегрирована в СУРЗ МВС.
Литература
1. Киселев Е.А. Построение информационного графа параллельной программы на основе данных профилирования и трассировки // Научный сервис в сети Интернет: экзафлопсное будущее: тр. Междунар. суперкомп. конф. (19–24 сентября 2011, г. Новороссийск). М.: Изд-во МГУ, 2011. С. 541–546.
2. Chou Chen-Ling, MarculescuRadu. Contention-aware Application Mapping for Network-on-Chip Communication Architectures. Computer Design, 2008. ICCD 2008. IEEE Intern. Conf. 2008.
3. NAS Parallel Benchmarks/ URL: http://www.nas.nasa. gov/publications/npb.html (дата обращения: 10.09.2012).
4. Аладышев О.С., Киселев Е.А., Корнеев В.В., Шабанов Б.М. Программные средства построения коммуникационной схемы многопроцессорной вычислительной системы. Высокопроизводительные вычислительные системы: матер. VII Междунар. науч. молодеж. школы. Таганрог: Изд-во ТТИ ЮФУ, 2010. С. 76–79.
5. Greening D.R. Parallel simulated annealing techniques, Emergent computation. 1991, pp. 293–306.
6. Баранов А.В., Киселев А.В., Киселев Е.А., Корнеев В.В., Семенов Д.В. Программный комплекс «Пирамида» организации параллельных вычислений с распараллеливанием по данным // Научный сервис в сети Интернет: суперкомпьютерные центры и задачи: тр. Междунар. суперкомп. конф. (20–25 сентября 2010, г. Новороссийск). М.: Изд-во МГУ, 2010. С. 299–302.
 , где T соответствует различным типам вычислительных устройств, а функция
, где T соответствует различным типам вычислительных устройств, а функция  ставит в соответствие вершине vi графа I тип вычислительного устройства, на котором может быть запущена ветвь с номером i;
ставит в соответствие вершине vi графа I тип вычислительного устройства, на котором может быть запущена ветвь с номером i;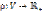 ; функция p(vi) ставит в соответствие вершине vi графа I количество вычислительных операций, выполненных ветвью с номером i.
; функция p(vi) ставит в соответствие вершине vi графа I количество вычислительных операций, выполненных ветвью с номером i.
 ставит в соответствие ребру eij графа
ставит в соответствие ребру eij графа 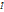 объем данных, переданный между ветвями с номерами i и j за время выполнения коммуникационного шаблона;
объем данных, переданный между ветвями с номерами i и j за время выполнения коммуникационного шаблона; ставит в соответствие ребру eij графа I число операций приема/передачи данных между ветвями с номерами i и j за время выполнения параллельной программы.
ставит в соответствие ребру eij графа I число операций приема/передачи данных между ветвями с номерами i и j за время выполнения параллельной программы. параллельной программы может быть описан с помощью матрицы смежности
параллельной программы может быть описан с помощью матрицы смежности 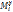 . Элемент eij матрицы
. Элемент eij матрицы 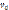

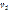











 граф ВС с номером j на уровне иерархии i (рис. 4а).
граф ВС с номером j на уровне иерархии i (рис. 4а). . В качестве вычислительного устройства типа T1 может выступать универсальный процессор, а вычислительного устройства типа T2 – графический процессор. МВС состоит из двух ВУ, каждый из которых содержит от двух до четырех многоядерных процессоров. Первый уровень
. В качестве вычислительного устройства типа T1 может выступать универсальный процессор, а вычислительного устройства типа T2 – графический процессор. МВС состоит из двух ВУ, каждый из которых содержит от двух до четырех многоядерных процессоров. Первый уровень 
 , образован низколатентной сетью (например InfiniBand), через которую взаимодействуют ВУ. На втором уровне иерархии, представленном графами
, образован низколатентной сетью (например InfiniBand), через которую взаимодействуют ВУ. На втором уровне иерархии, представленном графами  и
и  , для выполнения обменных операций между процессорами (ЦП) используется шина. Третий уровень образован вычислительными ядрами процессоров и представлен графами
, для выполнения обменных операций между процессорами (ЦП) используется шина. Третий уровень образован вычислительными ядрами процессоров и представлен графами  . Обмен данными между ядрами процессоров осуществляется через общую память.
. Обмен данными между ядрами процессоров осуществляется через общую память. :
: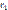








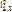





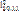



 матрицы
матрицы  , значит, прямой линии связи между вычислительными элементами ci и cj не существует.
, значит, прямой линии связи между вычислительными элементами ci и cj не существует. графа
графа  зададим отображения:
зададим отображения: , где T соответствует различным типам вычислительных устройств, а функция
, где T соответствует различным типам вычислительных устройств, а функция  ставит в соответствие вершине
ставит в соответствие вершине  тип
тип  вычислительного ядра p;
вычислительного ядра p; ; функция
; функция  ставит в соответствие вершине
ставит в соответствие вершине  – это линии связи, соединяющие между собой элементы графа
– это линии связи, соединяющие между собой элементы графа  , то есть
, то есть  где
где  . На множестве ребер Lk заданы отображения:
. На множестве ребер Lk заданы отображения: ; функция
; функция  ставит в соответствие ребру
ставит в соответствие ребру 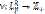 ; функция
; функция  ставит в соответствие ребру
ставит в соответствие ребру  ,
,  и
и  . На множестве ребер
. На множестве ребер  заданы отображения
заданы отображения 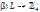 и
и  .
. , для которых выполняется условие (1). На множестве вершин V заданы отображения
, для которых выполняется условие (1). На множестве вершин V заданы отображения 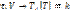 ,
,  и
и 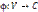 и представляется матрицей
и представляется матрицей 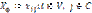 , где
, где 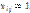 , если
, если  , и
, и  , если
, если 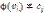 .
.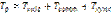 . (2)
. (2) , при котором
, при котором . (3)
. (3) выполнения
выполнения  вычислительных операций типа
вычислительных операций типа  ветвью
ветвью 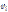 программы на вычислительном устройстве
программы на вычислительном устройстве  типа
типа  с производительностью
с производительностью  можно определить следующим образом:
можно определить следующим образом: (4)
(4) (5)
(5) информационного графа программы отображены на вершины
информационного графа программы отображены на вершины  графа ВС соответственно. Обозначим Lmn множество ребер, формирующих кратчайший путь от вершины cm к вершине cn. Тогда время выполнения обменных операций
графа ВС соответственно. Обозначим Lmn множество ребер, формирующих кратчайший путь от вершины cm к вершине cn. Тогда время выполнения обменных операций  между ветвями vi и vj можно вычислить по формуле
между ветвями vi и vj можно вычислить по формуле . (6)
. (6)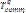 выполнения коммуникационного шаблона
выполнения коммуникационного шаблона  с графом
с графом  равно максимальной по длительности операции приема/передачи из данного шаблона:
равно максимальной по длительности операции приема/передачи из данного шаблона:
 (7)
(7) (8)
(8)
 (9)
(9)
 и значение счетчика итераций t равным 0.
и значение счетчика итераций t равным 0.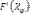 функционала (9).
функционала (9). . Если
. Если 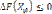 , вершина vi закрепляется за вершиной cj. Если
, вершина vi закрепляется за вершиной cj. Если  , закрепление вершины vi за вершиной cj осуществляется с вероятностью
, закрепление вершины vi за вершиной cj осуществляется с вероятностью  .
.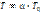 , где
, где  – параметр, влияющий на скорость понижения температуры, и перейти к шагу 3. Если зафиксирован выход функционала
– параметр, влияющий на скорость понижения температуры, и перейти к шагу 3. Если зафиксирован выход функционала  на стационарное значение или текущее значение T является конечным, завершить работу алгоритма. В остальных случаях увеличить значение j на 1 и перейти к шагу 4.
на стационарное значение или текущее значение T является конечным, завершить работу алгоритма. В остальных случаях увеличить значение j на 1 и перейти к шагу 4.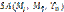 приведенный алгоритм отображения вершин информационного графа I на вершины графа ВС S с заданными начальной и конечной температурами соответственно.
приведенный алгоритм отображения вершин информационного графа I на вершины графа ВС S с заданными начальной и конечной температурами соответственно. Первые два способа распараллеливания алгоритма имитации отжига предполагают, что на каждом из вычислительных узлов доступна своя копия графа ВС и информационного графа программы. Данное условие может затруднять реализацию предложенных подходов для графов параллельной программы и ВС, которые невозможно целиком разместить в памяти одного ВУ. Поэтому для распараллеливания алгоритма имитации отжига был выбран способ, основанный на разбиении пространства поиска решений на независимые области.
Первые два способа распараллеливания алгоритма имитации отжига предполагают, что на каждом из вычислительных узлов доступна своя копия графа ВС и информационного графа программы. Данное условие может затруднять реализацию предложенных подходов для графов параллельной программы и ВС, которые невозможно целиком разместить в памяти одного ВУ. Поэтому для распараллеливания алгоритма имитации отжига был выбран способ, основанный на разбиении пространства поиска решений на независимые области. матрицу смежности информационного графа программы размера
матрицу смежности информационного графа программы размера  , а
, а 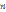 , где
, где  . Выполним декомпозицию графа ВС по ВУ путем разбиения матрицы
. Выполним декомпозицию графа ВС по ВУ путем разбиения матрицы  , часть матрицы
, часть матрицы  для k ВУ может быть описана следующим образом.
для k ВУ может быть описана следующим образом. элементов матрицы смежности графа ВС
элементов матрицы смежности графа ВС  для выполнения алгоритма моделирования отжига.
для выполнения алгоритма моделирования отжига.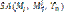 .
.