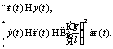Journal influence
Bookmark
Next issue
Realization of Lyapunov's method of first approximation in the program Maple 12
The article was published in issue no. № 4, 2012 [ pp. 150-152 ]Abstract:The research of stability of the solution of linear systems by using Lyapunov's method of first approximation is presented in the article. Also the properties of the solution are determined: is it stable or unstable, or will it be orbitally stable for the autonomous systems of ordinary differential equations that describe mechanical autonomous dynamic systems. In the article the software implementation of this method in the program Maple 12 is displayed. This method is an effective mean for the research of stability of difference equation systems and systems with aftereffect. Undeniable advantage of this method is following. The system of the differential equations can be investigated about stability without integration, but by constructing the special function with certain properties, and this function is depended from the right parts of the system. The developed program allows to test the system about noninteracting and to construct the phase portrait of the linearized system. This article shows the block scheme of the program and the algorithm of its realization. For clarity we consider the linear equation of free harmonic vibrations and use the program Maple 12 to solve the given task. As a result it has shown that the obtained system is autonomous, the phase portrait has been constructed, and we have revealed that orbital stability of the solution and the solution of the main system is also stable at any moment.
Аннотация:В статье представлены исследование устойчивости решения линейных систем c использованием метода Ляпунова по первому приближению с последующим выявлением свойств решения (устойчиво, неустойчиво, будет ли орбитально устойчиво для автономных систем обыкновенных дифференциальных уравнений, описывающих поведение динамических механических систем), а также программная реализация данного метода в Maple 12. Этот метод является эффективным средством исследования устойчивости разностных систем и систем с последействием. Его бесспорное преимущество в том, что систему дифференциальных уравнений можно исследовать на устойчивость не интегрированием, а построением специальной функции с определенными свойствами, зависящей от правых частей рассматриваемой системы. Разработанная программа позволяет осуществлять проверку системы на автономность и строить фазовый портрет линеаризованной системы. В статье представлены блок-схема программы и алгоритм ее реализации. Для наглядности рассмотрено линейное уравнение свободных гармонических колебаний. Результат решения поставленной задачи показал, что полученная система является автономной, построен фазовый портрет, а также выявлены орбитальная устойчивость решения в любой момент времени и то, что решение основной системы также устойчиво.
| Author: (lioness@pop3.ru) - | |
| Keywords: flowchart, phase portrait, autonomous system, program realization, universal method, stability |
|
| Page views: 12272 |
Print version Full issue in PDF (9.63Mb) Download the cover in PDF (1.26Мб) |
Движение (равновесие) механической системы можно найти в результате решения системы дифференциальных уравнений, которая может быть нелинейной и иметь высокий порядок. Нахождение ее решений, как правило, сопряжено с большими трудностями. На практике для исследования устойчивости решения нелинейных систем часто применяют метод исследования устойчивости соответствующих линейных систем.
К методу Ляпунова по первому приближению относятся такие способы решения, которые приводят к непосредственному исследованию возмущенного движения и в основании которых лежит анализ общих или частных свойств решений дифференциальных уравнений. Суть метода заключается в исследовании корней характеристического уравнения. Причем характеристическое уравнение задается в виде det(B‑lE)=0, где B – матрица коэффициентов системы, E – единичная матрица. Решение данного уравнения позволяет найти корни l. На основании общего решения задачи о возмущенном движении линейной системы можно сделать следующие выводы об устойчивости. 1. Если вещественные части всех корней характеристического уравнения отрицательны, li<0, i=1, 2, …, n, то линейная система асимптотически устойчива. 2. Если среди корней характеристического уравнения найдется хотя бы один с положительной вещественной частью, li>0, i=k, линейная система неустойчива. 3. Если в характеристическом уравнении нет корней с положительной вещественной частью, однако имеются корни с вещественными частями, равными нулю, li=0, i=1, 2, …, p£n, то линейная система просто устойчива, а l – точка покоя, центр [2]. Развитие компьютерной техники привело к необходимости автоматизации ее средствами анализа устойчивости. Это связано с тем, что процесс приближенного решения обыкновенного дифференциального уравнения проходит на компьютере, на основе компьютерных технологий строятся системы автоматического управления и автоматического регулирования. Отсюда возникает необходимость анализа устойчивости непосредственно в процессе компьютерного решения. В настоящей статье представлены программная реализация исследования устойчивости решения линейных систем в Maple 12 с помощью метода Ляпунова по первому приближению, а также построение фазовых портретов. Блок-схема программы приведена на рисунке 1. Алгоритм программы: with(LinearAlgebra); with(DEtools); printlevel := 0; a := 0; b := 1; c := -Pi^2; d := 0; «Система уравнений имеет вид»; px := a*x(t)+b*y(t); py := c*x(t)+d*y(t); 'dx/dt' = px; 'dy/dt' = py; sys := diff(x(t), t) = px, diff(y(t), t) = py; if autonomous({sys}, [x(t), y(t)], t) = true then print(«Данная система является автономной») else print(«Данная система является неавтономной») end if;
phaseportrait([sys], [x(t), y(t)], t = -10 .. 10, [[0, 1, -2], [0, -3, -3], [0, -2, 4], [0, 5, 5], [0, 5, -3], [0, -5, 2], [0, 5, 2], [0, -1, 2]], x = -30 .. 30, y = -20 .. 20, stepsize = .1, colour = blue, linecolor = black); «Матрица коэффициентов имеет вид»; A := Matrix([[a, b], [c, d]]); 'A' = A; «Характеристическое уравнение вида: det(A-λ*E) =0,»; B := Determinant(A-lambda*Matrix(2, 2, shape = identity)); B = 0; «Решение данного уравнения позволяет найти собственные числа λ»; k := solve(Determinant(A-lambda*Matrix(2, 2, shape = identity)) = 0, lambda); «Вещественные и мнимые части собственных чисел λ имеют вид»; havePositive := false; haveZero := false; ind := 0; for i in k do ind := ind+1; re := evalc(Re(i)); im := evalc(Im(i)); print(('Re')(ind) = re, ('Im')(ind) = im); if evalhf(re) > 0 then havePositive := true elif evalhf(re) = 0 then haveZero := true end if end do; if havePositive then print(«Таким образом, невозмущенное движение исходной нелинейной системы неустойчиво.») elif haveZero then print(«Таким образом, λ точка покоя — центр.») else print(«Таким образом, невозмущенное движение исходной нелинейной системы устойчиво в обычном смысле.») end if; Для наглядности рассмотрено линейное уравнение свободных гармонических колебаний:
С учетом того, что l=4 м, данное уравнение сведено к системе
В результате решения поставленной задачи выявлено следующее: данная система является автономной; фазовый портрет имеет вид, представленный на рисунке 2; имеет место орбитальная устойчивость решения в любой момент времени, решение основной системы тоже устойчиво. Сделанный вывод полностью согласуется с расчетами, выполненными в работе [3]. Программа написана для исследования устойчивости системы методом Ляпунова по первому приближению с последующим выявлением свойств решения: устойчиво, неустойчиво, будет ли орбитально устойчиво для автономных систем обыкновенных дифференциальных уравнений, описывающих поведение динамических механических систем. Данный метод является эффективным средством исследования устойчивости и стабилизации разностных систем, а также систем с последействием. Бесспорное преимущество этого метода в том, что систему дифференциальных уравнений можно исследовать на устойчивость не интегрированием, а построением специальной функции с определенными свойствами, зависящей от правых частей рассматриваемой системы. В заключение отметим, что разработанные алгоритм и методика автоматизации позволяют исследовать линеаризованную систему на устойчивость, осуществлять проверку системы на автономность, а также строить фазовый портрет. А это, в свою очередь, облегчает процедуру получения расчетов для определения динамической устойчивости деформируемых систем. Литература 1. Вольмир А.С. Устойчивость упругих систем. М.: Физматгиз, 1963. 879 с. 2. Попов Д.Н. Динамика и регулирование гидро- и пневмосистем. М.: Машиностроение, 1987. 464 с. 3. Кудинов А.Н., Катулев А.Н., Кузнецов А.Ю. Исследование устойчивости автономных нелинейных динамических систем // Динамические и технологические проблемы механики конструкций и сплошных сред: матер. XVI Междунар. симпоз. М., 2010. С. 110–112. |
| Permanent link: http://swsys.ru/index.php?id=3330&lang=en&page=article |
Print version Full issue in PDF (9.63Mb) Download the cover in PDF (1.26Мб) |
| The article was published in issue no. № 4, 2012 [ pp. 150-152 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Программная реализация универсального метода исследования устойчивости деформируемых систем в Maple
- Управление развитием надежных кластерных структур информационных систем
- Алгоритм и программная реализация имитационной модели гравитационного сепаратора колонного струйно-эмульсионного реактора
- Имитационное моделирование многофазных многокомпонентных систем в потоке газа
- Программная реализация цифровой обработки данных силового трансформатора
Back to the list of articles
 Возможность суждения об устойчивости или неустойчивости первоначальной нелинейной системы на основании рассмотрения уравнений первого приближения, то есть линеаризованной системы уравнений возмущенного движения, впервые была рассмотрена А.М. Ляпуновым [1]. При этом найденные и доказанные им положения об устойчивости линеаризованной системы получаются из его общей теории об устойчивости и неустойчивости.
Возможность суждения об устойчивости или неустойчивости первоначальной нелинейной системы на основании рассмотрения уравнений первого приближения, то есть линеаризованной системы уравнений возмущенного движения, впервые была рассмотрена А.М. Ляпуновым [1]. При этом найденные и доказанные им положения об устойчивости линеаризованной системы получаются из его общей теории об устойчивости и неустойчивости.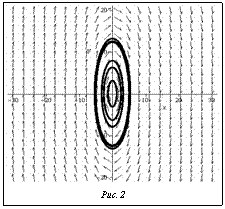 «Фазовый портрет этой системы»;
«Фазовый портрет этой системы»;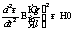 , где
, где  .
.