Journal influence
Bookmark
Next issue
Software package for integer lattices basis reduction
The article was published in issue no. № 4, 2012 [ pp. 180-183 ]Abstract:This article presents short survey of LLL and BKZ lattice reduction algorithms. Paper contain presents LRT software package for solving SVP and SBP integer lattice problems and generating Goldstein–Mayer lattices. LRT was used to reduce basis of sample lattices for testing algorithms that solve the shortest vector problem (SVP) in euclidean lattices. Were obtained accurate solutions, with error less than 6,1 % of the length of the shortest vector integer lattices (corresponding of Minkowski upper bound) for dimensions 58, 62, 69, 71, 74, 81, solutions took 84, 77, 68, 65, 60, 49 places in the contest algorithms respectively. At 100th dimension of the integer lattice, 32 vectors block size and quadrupleprecision floating-point format, software package LRT effective fpLLL and NTL by 17,2 %, 24,3 %, respectively. LRT is fully compatible with Windows OS and freeware.
Аннотация:Описаны алгоритм Ленстры–Ленстры–Ловаса (LLL-алгоритм) и блочный алгоритм Коркина–Золотарева (BKZ- алгоритм) приведения базиса целочисленных решеток с произвольным фактором. Данные алгоритмы совместно с модулем генерации случайных решеток, сложных в смысле Гольдштейна–Майера, положены в основу программного комплекса LRT, предназначенного для решения задач криптографии, линейного программирования, управления, теории информации и кодирования. Результаты работы приложения апробированы на конкурсе алгоритмов поиска кратчайшего вектора целочисленных решеток. Были получены уточненные и точные решения с погрешностью менее 6,1 % от длины кратчайшего вектора целочисленных решеток (соответствующей верхней оценке Минковского) для размерностей 58, 62, 69, 71, 74, 81, занявшие соответственно 84, 77, 68, 65, 60, 49-е места на конкурсе алгоритмов. При 100-й размерности целочисленной решетки, 32-векторном размере блока и четырехкратной точности вычислений программный комплекс LRT эффективнее fpLLL и NTL на 17,2 % и 24,3 % соответственно. Реализованный программный комплекс LRT работает на платформе семейства ОС Windows и свободно распространяется в бинарном виде.
| Authors: Kuzmin O.V. (quzminov@mail.ru) - Institute of Mathematics, Economics and Informatics of Irkutsk State University, Irkutsk, Russia, Ph.D, Usatyuk V.S. (L@Lcrypto.com) - Bratsk State University, Bratsk, Russia | |
| Keywords: , block korkin-zolotarev reduction, shortest vector problem, shortest basis problem, integer lattices, lattice basis reduction |
|
| Page views: 11187 |
Print version Full issue in PDF (9.63Mb) Download the cover in PDF (1.26Мб) |
Математический аппарат теории решеток тесно связан с абстрактной и геометрической алгеброй, теорией информации, оптимизацией и криптоанализом. Это обстоятельство позволяет использовать данный аппарат для решения задач линейного программирования, плотной упаковки тел (в частности для Евклидова пространства – сфер) [1], факторизации многочленов с рациональными коэффициентами [2], поиска диофантовых приближений [3], оптимизации кодирования с использованием адаптивных антенных решеток со слабо коррелированными антенными элементами (MIMO) [4], криптоанализа RSA- и DSA-систем и некоторых типов генераторов случайных чисел [2], синтеза криптографических примитивов и протоколов на основе теории решеток [5]. Решетка – дискретная аддитивная подгруппа, заданная на множестве Rn. Решетку L можно представить как множество целочисленных линейных комбинаций L(b1, …, b2)= Решетки L1, L2, заданные базисами Пусть имеется радиус сферы, заданный нормой p. Под i-м минимумом
Дефектом ортогонализации решетки L, образованной базисом Задача приближенного поиска кратчайшего вектора (g-approximate shortest vector problem, Задача приближенного поиска кратчайшего базиса (g-approximate shortest basis problem,
Для решения LLL-алгоритм приведения базиса решетки [8]. Вход: базис решетки L(B), LÌZn и dÎ(0,25, 1), D. Выход: приведенный LLL-базис. 1. Ортогонализация Грама–Шмидта, b*ÎB* – ортогональный вектор базиса. 2. Редукция векторов базиса: "i,j: 2£i£m, i-1³j³1. 3. Перестановка векторов bi и bi+1 и возврат к шагу 1, если BKZ-алгоритм приведения базиса решетки [8]. Вход: базис решетки L(B), LÌZn и b£n (L(B¢), образованный b-векторами из L(B)), D. Выход: приведенный BKZ-базис решетки. 1. Применение LLL-алгоритма для предварительного приведения базиса решетки. 2. Выполнять в цикле k=1, …, m–b+1: – перечислительным методом (ENUM) решаем – если – иначе LLL-приведение следующего блока векторов. 3. Вывод базиса, если после нескольких проходов по всему базису его длина не меняется. Модифицированный алгоритм Грама–Шмидта (MGS) [9]. Вход: базис решетки L(B)ÎZnxm. Выход: Q=(q1, q2, …, qm) – ортогональный базис, 1. Выполнить в цикле i=1, …, m: 2. Выполнить в цикле i=1, …, m: – – выполнить в цикле j=i+1, …, m: В приложении LRT были реализованы оба алгоритма приведения базиса решеток, что позволяет осуществлять приведение базиса с произвольной точностью g [10]. Для ортогонализации применяется вычислительно устойчивый модифицированный алгоритм ортогонализации MGS. Последнее обстоятельство обусловливает последовательный характер работы приложения LRT. Приложение написано на языке Си с применением глубокой оптимизации посредством среды интерактивной разработки Microsoft Visual C++ 2010 Express Version 10.0.40219.1 SP1Rel. Ввод-вывод данных осуществляется на основе работы с текстовыми файлами базиса решетки и отчета о результате работы приложения. В приложении доступно изменение параметров D – точности промежуточных результатов, d для алгоритма LLL и размера блока b для алгоритма BKZ. Для реализации произвольной точности вычислений применяется библиотека MIRACL, переданная авторам статьи Майклом Скоттом для некоммерческого использования в 2006 году. Применение этой библиотеки позволяет изменять точность промежуточных результатов D от однократной float (7 знаков), двукратной double (15 знаков), четырехкратной quad (34 знака) до 1,7×106 десятичных знаков. С целью повышения устойчивости работы приложения при высокой точности вычислений и большой размерности приводимых целочисленных решеток был реализован собственный планировщик памяти, лишенный проблемы отказа функции realloc, уменьшающий число обращений к менеджеру памяти ОС. Результаты работы программы апробированы на 40 задачах конкурса алгоритмов поиска коротких векторов с фактором g=1,05 на решетках с размерностью 50–90 и приведение базиса 512-, 1024-, 2048-мерных целочисленных решеток с экспоненциальной точностью [11].
На основе приведения базиса решеток, сложных по Гольдштейну–Майеру, было осуществлено сравнение программного комплекса LRT (ver. 1.0) с библиотеками NTL (ver. 5.2.2), fpLLL (ver. 3.1.1). Сравнение осуществлялось на ПК Phenom X4 965/ 8 Gb DDR2 800, ОС Microsoft Windows 7 x64 SP1. Для сравнения применялся BKZ-алгоритм приведения базиса целочисленных решеток, размерность которых n=50, …, 100, с шагом 10, длина представления координатного компонента в десятичных знаках была равна 15, b=32, D равна четырехкратной точности числа с плавающей запятой (34 десятичных знака). Результаты сравнения приведены на рисунке. С ростом размерности базиса целочисленной решетки растет эффективность комплекса LRT. При размерности n=100 LRT эффективнее fpLLL и NTL на 17,2 % и 24,3 % соответственно. Комплекс LRT является эффективным средством в классе последовательных реализаций для решения означенных выше задач. Он обеспечивает высокую числовую устойчивость результатов и возможность работы с целочисленными решетками больших размерностей. Следующим шагом в развитии программного комплекса LRT станет применение в нем параллельных алгоритмов ортогонализации на основе OpenCL, NVIDIA CUDA, AMD Core Math Library и Intel Math Kernel Library. Литература 1. Conway J.H., Sloane N.J.A. Sphere Packings, Lattices and Groups. Springer. 3rd edition, 1999, 703 p. 2. Dwork C. Lattices and their Application to cryptography [Lecture Notes] Stanford University. 1998, 116 p. 3. Grotschel M., Lovasz L., Schrijver A. Geometric Algorithms and Combinatorial Optimization. Springer-Verlag, 1993, 564 p. 4. Mobasher A. Applications of Lattice Codes in Communication Systems. Canadian theses. University of Waterloo. Dept. of Electrical and Computer Engineering, 2008, 147 p. 5. Bernstein D.J., Buchmann J., Dahmen E. (eds.). Post Quantum Cryptography. Springer, 2009, pp. 147–191. 6. Press W.H., Teukolsky S.A., Vetterling W.T. Numerical Recipes: The Art of Scientific Computing. New York: Cambridge University Press. 2007. 1262 p. 7. Lenstra A.K., Lenstra H.W., Lovasz 8. Schnorr C.P., Euchner M. Lattice basis reduction: Improved practical algorithms and solving subset Sum Problems. Fundamentals of Computation Theory, 1991, pp. 68–85. 9. Higham N.J. Accuracy and Stability of Numerical Algorithms Society for Industrial and Applied Mathematics, 2002, 711 p. 10. Комплекс LRT. URL: http://www.lcrypto.com/lsolv/ (дата обращения: 1.06.2012). 11. Lattice challenge. URL: http://www.latticechallenge.org/ (дата обращения: 1.06.2012). 12. Goldstein D., Mayer A. On the equidistribution of Hecke points. Forum Mathematicum. 2003. Vol. 15, no. 2, pp. 165–189. |
| Permanent link: http://swsys.ru/index.php?id=3338&lang=en&page=article |
Print version Full issue in PDF (9.63Mb) Download the cover in PDF (1.26Мб) |
| The article was published in issue no. № 4, 2012 [ pp. 180-183 ] |
Perhaps, you might be interested in the following articles of similar topics:
 n линейно независимых базисных векторов
n линейно независимых базисных векторов  в m-мерном евклидовом пространстве, где m и n – размерность и ранг решетки соответственно. Решетки, у которых размерность и ранг равны, называются полноразмерными.
в m-мерном евклидовом пространстве, где m и n – размерность и ранг решетки соответственно. Решетки, у которых размерность и ранг равны, называются полноразмерными. ,
,  , конгруэнтны,
, конгруэнтны,  , если объемы фундаментальных параллелепипедов, образованных их базисами, равны
, если объемы фундаментальных параллелепипедов, образованных их базисами, равны  , где
, где  или
или  для полноразмерных решеток. Множество таких базисов Bi может быть получено в результате умножения приведенного базиса решетки Li на целочисленные унимодулярные матрицы.
для полноразмерных решеток. Множество таких базисов Bi может быть получено в результате умножения приведенного базиса решетки Li на целочисленные унимодулярные матрицы. будем понимать наименьший радиус сферы, содержащий i линейно независимых базисных векторов решетки. Длине кратчайшего вектора в решетке L соответствует
будем понимать наименьший радиус сферы, содержащий i линейно независимых базисных векторов решетки. Длине кратчайшего вектора в решетке L соответствует  . Из теоремы Минковского о последовательных минимумах следует верхняя оценка длины векторов n-мерной решетки L:
. Из теоремы Минковского о последовательных минимумах следует верхняя оценка длины векторов n-мерной решетки L: ,
,  , где
, где  – константа Эрмита.
– константа Эрмита. , называют скалярную величину
, называют скалярную величину  . Путем унитарных преобразований исходного базиса можно получить ортогональный базис решетки, конгруэнтный исходной. Легко убедиться в том, что полученный ортогонализуемый базис
. Путем унитарных преобразований исходного базиса можно получить ортогональный базис решетки, конгруэнтный исходной. Легко убедиться в том, что полученный ортогонализуемый базис  дает нижнюю оценку длины кратчайшего вектора исходной n-мерной решетки L:
дает нижнюю оценку длины кратчайшего вектора исходной n-мерной решетки L: bÎ1, …, n. Ортогональный базис решетки может быть получен QR-методами разложения матрицы базиса решетки: Грама–Шмидта, Гивенса, Хаусхолдера [6].
bÎ1, …, n. Ортогональный базис решетки может быть получен QR-методами разложения матрицы базиса решетки: Грама–Шмидта, Гивенса, Хаусхолдера [6]. ): пусть даны m-мерная решетка L ранга n и вещественный g>0. Найти ненулевой вектор, в g раз больший кратчайшего вектора
): пусть даны m-мерная решетка L ранга n и вещественный g>0. Найти ненулевой вектор, в g раз больший кратчайшего вектора  .
. : пусть дана m-мерная решетка L ранга n. Найти базис
: пусть дана m-мерная решетка L ранга n. Найти базис

 с экспоненциальной точностью
с экспоненциальной точностью  достаточно привести базис к d‑LLL-редуцированному базису, применив полиномиальный по временной сложности алгоритм Ленстры–Ленстры–Ловаса (LLL) [7]. Для решения
достаточно привести базис к d‑LLL-редуцированному базису, применив полиномиальный по временной сложности алгоритм Ленстры–Ленстры–Ловаса (LLL) [7]. Для решения  достаточно привести подмножество базиса решетки, состоящее из b£n-векторов, к базису Коркина–Золотарева, применив блочный алгоритм Коркина–Золотарева (BKZ), чья временная сложность зависит от размера блока, изменяясь от полиномиальной до экспоненциальной.
достаточно привести подмножество базиса решетки, состоящее из b£n-векторов, к базису Коркина–Золотарева, применив блочный алгоритм Коркина–Золотарева (BKZ), чья временная сложность зависит от размера блока, изменяясь от полиномиальной до экспоненциальной. .
. .
.
 , вставка найденного вектора в начало текущего блока и удаление ли- нейной зависимости векторов в нем
, вставка найденного вектора в начало текущего блока и удаление ли- нейной зависимости векторов в нем  ;
; верхняя треугольная матрица.
верхняя треугольная матрица. .
.
 ,
, 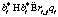 .
. Для задач шифрования и кодирования возникает необходимость построения решеток, сложных по Гольдштейну–Майеру, то есть случайных плотных решеток, построенных на основе некоторого заранее известного короткого базиса [12]. Для решения задач такого класса в приложение LRT был добавлен входной параметр, позволяющий генерировать решетки заданной размерности, сложные по Гольдштейну–Майеру.
Для задач шифрования и кодирования возникает необходимость построения решеток, сложных по Гольдштейну–Майеру, то есть случайных плотных решеток, построенных на основе некоторого заранее известного короткого базиса [12]. Для решения задач такого класса в приложение LRT был добавлен входной параметр, позволяющий генерировать решетки заданной размерности, сложные по Гольдштейну–Майеру. . Factoring polynomials with rational coefficients. Math. Ann., 1982. Vol. 261, no. 4, pp. 515–534.
. Factoring polynomials with rational coefficients. Math. Ann., 1982. Vol. 261, no. 4, pp. 515–534.