Journal influence
Bookmark
Next issue
Use the linear programming for cad designing of additional aerodynamic surfaces
The article was published in issue no. № 4, 2012 [ pp. 203-206 ]Abstract:The method of automatized designing with developed program resources and optimal choice of additional aerodynamic surfaces by the production costs criterion for main aircraft providing with maximum aerodynamic efficiency for the specific type of main aircraft was formulated and justified in the article. The method is based on developed algorithm using linear programming namely the simplex method. The task solution process of linear programming by the simplex method has the iterative process, i.e. the calculation procedures of the same type and repeated in specific sequence before the optimal solution will not get. As the model has some variables the task can be solved in diagram form. The diagram method usage is in geometric representation, acceptable solutions, in which all model confines are satisfied simultaneously. The offered methods can distinguish the next features of considered method, the realization of which gets the new capabilities in task solutions of fleet’s management of main aircraft with program resources for computer. This methods allows to identity the need tape of additional aerodynamic surfaces for the main aircraft of the same type to get the economic interpretation of obtained solution.
Аннотация:В представленной статье сформулирован и обоснован метод автоматизированного проектирования с использованием разработанных программных средств и оптимального выбора дополнительных аэродинамических поверхностей по критерию производственных расходов для магистральных воздушных судов, обеспечивающих максимальную аэродинамическую эффективность конкретного типа воздушного судна. Метод основан на разработанном алгоритме с применением линейного программирования – симплекс-метода. Процесс решения задачи линейного программирования симплекс-методом носит итерационный характер, тот есть однотипные вычислительные процедуры повторяются в определенной последовательности до тех пор, пока не будет получено оптимальное решение. В связи с тем, что модель содержит незначительное количество переменных, задачу можно решить графически. Использование графического метода заключается в геометрическом представлении допустимых решений, то есть в построении области допустимых решений, в которых одновременно удовлетворяются все ограничения модели. Предлагаемая методика позволяет определить потребный тип дополнительной аэродинамической поверхности для конкретного типа магистрального воздушного судна, дать экономическую интерпретацию полученного решения.
| Authors: (gorbynovaleks@mail.ru) - , Russia, Pripadchev A.D. (aleksejj-pripadchev@rambler.ru) - Orenburg State University (Associate Professor), Orenburg, Russia, Ph.D | |
| Keywords: the range of permissible decisions, optimization models, simplex-method, the coefficient of aerodynamic efficiency, additional aerodynamic surfaces, linear programming, aircrafts |
|
| Page views: 10342 |
Print version Full issue in PDF (9.63Mb) Download the cover in PDF (1.26Мб) |
Авиапредприятия остро нуждаются в современных воздушных судах (ВС) с эффективной аэродинамикой, позволяющей снизить аэродинамическое сопротивление на крейсерском режиме полета до 20 %, что, в свою очередь, приведет к снижению удельного расхода топлива [1] и к уменьшению потребной взлетной дистанции с полной коммерческой загрузкой. Поставленную задачу призваны решить дополнительные аэродинамические поверхности [2], процесс проектирования которых невозможен без применения современных компьютерных технологий и методов системного анализа и исследования операций. Необходимо определить оптимальную дополнительную аэродинамическую поверхность крыла, проектирование которой осуществляется с использованием разработанных авторами програм- мных средств (Свид. о гос. регистрации программ для ЭВМ № 2012616409, 2012614559), по критерию производственных расходов для магистрального ВС, обеспечивающую максимальную аэродинамическую эффективность [3] для конкретного типа ВС. Решение поставленной задачи дает ответ на вопрос, какой тип дополнительной аэродинамической поверхности экономически эффективен на конкретном типе ВС в процессе пассажирских перевозок. Рассмотрим сущность и особенности предлагаемого метода оптимизации на основе критерия производственных расходов ВС. Методологическая и программная реализация заключается в определении оптимального типа дополнительной аэродинамической поверхности n на конкретном типе магистрального ВС. Целевой функцией является сумма производственных расходов на все рейсы для всех типов дополнительных аэродинамических поверхностей при сохранении показателя дохода при выполнении системы ограничения неравенств. Получаем задачу линейного программирования, которую решаем симплекс-методом. Переменными являются ко- личество дополнительных аэродинамических поверхностей n и тип ВС m. Ограничениями выступает система ограничений-равенств для всех дополнительных аэродинамических поверхностей. Процесс решения задачи линейного программирования симплекс-методом носит итерационный характер, который заключается в том, что однотипные вычислительные процедуры повторяются в определенной последовательности до тех пор, пока не будет получено оптимальное решение [3]. Для методологического построения решения за- дачи линейного программирования математическая модель структуры парка ВС представлена в стандартной форме линейных оптимизационных моделей, при этом все ограничения записываются в виде равенства с неотрицательной правой частью, значения всех переменных модели неотрицательны, целевая функция подлежит минимизации. В процессе построения математической модели для решения данной задачи необходимо четко представлять, для определения каких величин должна быть построена математическая модель; какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, характерные для моделирующего процесса определения оптимальной дополнительной аэродинамической поверхности для конкретного типа ВС; какие переменные, соответствующие оптимальному решению задачи, необходимо выбрать. Трудность построения математической модели заключается в идентификации переменных и последующем представлении цели и ограничений в виде математических функций этих переменных. В данном случае имеем дополнительные аэродинамические поверхности, установленные на типах ВС m=1, 2, …, М, где m – тип ВС, и коэффициенты аэродинамической эффективности при использовании дополнительной аэродинамической поверхности n=1, 2, …, N. Количество дополнительных аэродинамических поверхностей на 1-м типе ВС обозначим X1.1, на 2-м типе ВС – X1.2, на i-м типе ВС j-го типа – Xi.j, где i=1, 2, …, n, j=1, 2, …, m. Количество дополнительных аэродинамических поверхностей на 1-м типе ВС за один рейс на i-м ВС j-го типа обозначим ai.j, где i=1, 2, …, n, а j=1, 2, …, m. Расходы на один рейс на i-й дополнительной аэродинамической поверхности ВС j-го типа обозначим ci.j, где i=1, 2, …, n, j=1, 2, …, m; каждую дополнительную аэродинамическую поверхность, установленную на ВС всех типов, – 1, 2, …, М. Тогда для первого ВС коэффициент аэродинамической эффективности вычисляем по формуле
для второго ВС
Окончательно для всех ВС составляем систему ограничений-равенств:
где Общую сумму расходов на все рейсы всех дополнительных аэродинамических поверхностей вычисляем по формуле
Если необходимо минимизировать общую сумму расходов по формуле (4) при выполнении системы ограничений-равенств (3), то получаем задачу линейного программирования, то есть этим методом находим После определения Если к системе ограничений-равенств добавить систему ограничений-равенств (неравенств) по количеству рейсов каждого типа, получим общее количество рейсов К для всех дополнительных аэродинамических поверхностей типа 1:
Общее количество рейсов для всех дополнительных аэродинамических поверхностей типа 2:
Окончательно получим систему ограничений-равенств по общему количеству рейсов для всех дополнительных аэродинамических поверхностей для каждого типа ВС:
Добавляя к системе ограничений (1) систему (7), можно минимизировать общую сумму расходов (4). В результате опять получаем задачу линейного программирования, которую решаем симплекс-методом. Для решения необходимо задать В связи с тем, что модель содержит незначительное количество переменных, задачу можно решить графически. Использование графического метода заключается в геометрическом представлении допустимых решений, то есть в построении области допустимых решений, в которых одновременно удовлетворяются все ограничения модели. В каждой точке, принадлежащей внутренней области, все ограничения выполняются, поэтому решения, соответствующие этим точкам, являются допустимыми. Пространство решений содержит бесконечное число таких точек, но, несмотря на это, можно найти потребное решение [4]. Оптимальная дополнительная аэродинамическая поверхность и аэродинамическая эффективность представлены в таблице. Выбор дополнительной аэродинамической поверхности
Результаты исследования внедрены на предприятиях государственной авиации РФ и в научно-производственных объединениях, то есть в научную и проектную деятельность Научно-внедренческого центра Международного исследовательского института, ОАО «Оренбургские авиалинии», в учебный процесс Аэрокосмического института Оренбургского государственного университета. Все вышеизложенное позволяет выделить следующие отличительные особенности рассмотренного метода, реализация которого предоставляет новые возможности для решения задач управления парком ВС авиапредприятия. Информация, полученная с помощью симплекс-метода, не ограничивается лишь значениями переменных. Это означает, что метод позволяет дать экономическую интерпретацию полученного решения. В результате решения уравнения (4) с системой ограничений (3) и (7) при помощи програм- много средства, разработанного Припадчевым А.Д. (Свид. о гос. регистрации программы для ЭВМ № 2010611242), выбираем наилучший тип дополнительной аэродинамической поверхности из предлагаемой классификации дополнительных аэродинамических поверхностей [2] для конкретного типа ВС. Предлагаемая методика с программным средством для ЭВМ позволяет определить потребный тип дополнительной аэродинамической поверхности для конкретного типа магистрального ВС. Литература 1. Краснов Н.Ф. Аэродинамика. Основы теории. Аэродинамика профиля и крыла: учебник для втузов. М.: Эдиториал УРСС, 2010. Ч. 1. 496 с. 2. Горбунов А.А., Припадчев А.Д. Повышение аэродинамической эффективности воздушного судна путем внедрения дополнительных аэродинамических поверхностей в виде законцовок крыла // Народное хозяйство. Вопросы инновационного развития. 2012. № 1. С. 222–224. 3. Аэрокосмическое обозрение: аналитика, комментарии, обзоры. 2008. № 5. С. 54–57. 4. Припадчев А.Д. Определение оптимального парка воздушных судов. М.: Академия естествознания, 2009. 246 с. |
| Permanent link: http://swsys.ru/index.php?id=3343&lang=en&page=article |
Print version Full issue in PDF (9.63Mb) Download the cover in PDF (1.26Мб) |
| The article was published in issue no. № 4, 2012 [ pp. 203-206 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Моделирование парка воздушных судов методом линейного программирования
- Построение и оптимизация производственной программы разделительного комплекса
- Поиск решения задачи целочисленного программирования с помощью итеративного округления координат
- Кластеризация атомарных знаний с использованием методов линейной оптимизации
- Программная реализация метода автоматизированного проектирования фюзеляжа воздушного судна с помощью объектно-ориентированных технологий
Back to the list of articles
 , (1)
, (1) . (2)
. (2) , (3)
, (3) – известные величины,
– известные величины,  ,
,  ;
;  – известные величины,
– известные величины,  . (4)
. (4) , где
, где  , зная расстояние и скорость, определяем оптимальную дополнительную аэродинамическую поверхность для конкретного типа ВС для узла перевозок А.
, зная расстояние и скорость, определяем оптимальную дополнительную аэродинамическую поверхность для конкретного типа ВС для узла перевозок А. . (5)
. (5) (6)
(6) . (7)
. (7) ,
,  ,
, 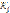 ,
, 
