Journal influence
Higher Attestation Commission (VAK) - К1 quartile
Russian Science Citation Index (RSCI)
Bookmark
Next issue
№4
Publication date:
09 December 2024
Mathematical modelling of thermal processes in layered structures
The article was published in issue no. № 1, 2013 [ pp. 129-132 ]Abstract:One of the major factors promoting increase of efficiency of functioning of units of continuous molding of preparations, ensuring working capacity and optimum technological operating modes of the equipment is. For increase in service life of crystallizers now resort to certain technological modifications of their working walls. This improvement of quality of a surface of a crystallizer at the expense of use of special alloys or coverings on a surface of a copper wall. Physical and mathematical simulation of thermal process of system «metal melt–a coating–a crystallizer pan wall» at the moment of steel priming is in-process presented. The software product which use allows to track character of an establishment of a temperature field at a heatstroke at the moment of steel pouring is developed for mathematical modelling; to analyse a temperature field from time in a covering and a wall of a crystallizer and to define the maximum size of temperature. The results received during use of the software product, were used at a choice of optimum modes of a covering from nickel on an internal wall of a crystallizer for increase of wear resistance of the equipment without decrease in quality of finished goods.
Аннотация:Одним из основных факторов, способствующих повышению эффективности функционирования агрегатов не-прерывного литья заготовок, является обеспечение работоспособности и оптимальных технологических режимов работы оборудования. Для увеличения срока службы кристаллизатора машин непрерывного литья заготовок в настоящее время прибегают к определенным технологическим модификациям их рабочих стенок. Это улучшение качества поверхности кристаллизатора за счет использования специальных сплавов либо нанесение покрытий на поверхность медной стенки. В работе представлено физико-математическое моделирование теплофизического процесса системы «расплав металла–покрытие–стенка кристаллизатора» в момент заливки стали. Для математического моделирования разработан программный продукт, использование которого позволяет проследить характер установ-ления температурного поля при тепловом ударе в момент заливки стали, проанализировать температурное поле в зависимости от времени в покрытии и стенке кристаллизатора и определить максимальную величину температуры. Результаты, полученные в ходе использования программного продукта, были использованы при выборе оптимальных режимов нанесения защитно-восстановительного покрытия из никеля на внутреннюю стенку кристаллизатора машины непрерывного литья заготовок, способствующих повышению износоустойчивости оборудования без снижения качества готовой продукции.
| Authors: () - , (egorov-lyudmil@yandex.ru) - , Russia, (egorov-lyudmil@yandex.ru) - , Russia | |
| Keywords: mathematical modelling, software product, a crystallizer pan wall, an inoculating coating, a tempering |
|
| Page views: 10779 |
Print version Full issue in PDF (5.29Mb) Download the cover in PDF (1.21Мб) |
| Permanent link: http://swsys.ru/index.php?id=3399&lang=en&page=article |
Print version Full issue in PDF (5.29Mb) Download the cover in PDF (1.21Мб) |
| The article was published in issue no. № 1, 2013 [ pp. 129-132 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Программное обеспечение автоматизированной системы управления электронно-лучевой сваркой тонкостенных конструкций
- Моделирование температурных полей в многослойных структурах
- Программы моделирования температурных полей в изделиях плоской формы
- Применение Interactive Data Language для обработки данных радиометрических измерений
- Анализ особенностей процессов управления требованиями к информационным системам государственных структур
Back to the list of articles
 (1)
(1) , (2)
, (2) , (3)
, (3)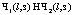 , (4)
, (4) , (5)
, (5)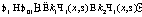 , (6)
, (6)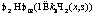 , (7)
, (7) .
.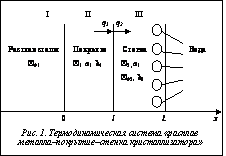 Для задачи моделирования теплового состояния в системе «защитное покрытие–рабочая стенка» кристаллизатора объектом исследования является температурное поле покрытия и рабочей стенки, изменяющееся в пространстве и времени. По результатам математического моделирования получим зависимости температуры покрытия по толщине во времени, температуры границ покрытия с металлом и кристаллизатором, зависимости изменения температуры от времени. По этим зависимостям можно сделать вывод о поведении температурного поля, вынести решение о выборе параметров для расчета. Диаграмма функциональной модели изменения температурного поля в покрытии и рабочей стенке кристаллизатора представлена на рисунке 2.
Для задачи моделирования теплового состояния в системе «защитное покрытие–рабочая стенка» кристаллизатора объектом исследования является температурное поле покрытия и рабочей стенки, изменяющееся в пространстве и времени. По результатам математического моделирования получим зависимости температуры покрытия по толщине во времени, температуры границ покрытия с металлом и кристаллизатором, зависимости изменения температуры от времени. По этим зависимостям можно сделать вывод о поведении температурного поля, вынести решение о выборе параметров для расчета. Диаграмма функциональной модели изменения температурного поля в покрытии и рабочей стенке кристаллизатора представлена на рисунке 2.

