В настоящее время сеть Интернет демонстрирует впечатляющие темпы роста во всем мире. С увеличением количества пользователей сети появляется все больше интернет-сервисов, предоставляющих широкий спектр самых разнообразных возможностей, одной из которых является пере- дача потоков данных большого объема, прежде всего потоков медиаинформации. Согласно исследованию компании Cisco «Индекс развития ви- зуальных сетевых технологий в период с 2011 по 2016 гг.» [1], в последнее время наблюдается многократный рост IP-трафика благодаря популярности новых интерактивных медиарешений и стремительному увеличению объема видеоконтента. В частности, на 2011 год объем видеотрафика превысил 50 % и к 2016 году эта цифра будет только увеличиваться [1]. При этом все чаще разработчики сетей передачи медиапотоков используют пиринговую технологию для повышения качества передаваемого видеоконтента. Поскольку качество звука и изображения определяется объемом получаемых в единицу времени данных (битрейтом), наработки при создании пиринговых файлообменных сетей, позволяющие обмениваться файлами с высоким битрейтом, нашли применение и при передаче медиапотоков.
Суть пирингового подхода состоит в том, что узел может получать потоки данных не только от сервера, но и от других узлов. Распределение потоков на основе пиринговой сети позволяет построить более высокопроизводительную систему, чем использование централизованного сервера-хранилища видеоконтента. Однако в этом случае необходимо определить логические связи между пользователями, в соответствии с которыми будет производиться обмен медиаданными. От топологии этих связей напрямую зависит и общая производительность системы. Правильный выбор логических связей позволит повысить средний битрейт потоков. В последние годы проводится много исследований в данной области и публикуется большое количество материалов на эту тему (в основном в западных изданиях). В настоящей статье предлагается новый способ решения проблемы выбора логических связей сети распределения данных потокового вещания на основе пирингового подхода.
Учет сетевой топологии для распределения потоков
В основе большинства пиринговых технологий распределения потоков [2–5] лежит закон случайного равномерного распределения каждому из узлов партнеров по обмену трафиком, то есть логические связи обмена данными между узлами в сети устанавливаются случайным образом, без оценки возможностей тех или иных узлов и без учета их местоположения. Каждый партнер передает узлу те фрагменты потока, которых у последнего нет. Из совокупности фрагментов складывается целевой медиапоток. В целом использование такого децентрализованного подхода на практике показало неплохие результаты. Например, система CoolStreaming [2] в 2006 году насчитывала один миллион пользователей из Европы и США. Средний битрейт при этом составлял 450 Кбит/с. Схожие результаты демонстрировали в 2008 году китайские системы PPLive [4] и PPStream [5].
Однако основным недостатком такого рода систем распределения потоков является то, что партнеры для каждого узла выбираются случайным образом, как бы далеко друг от друга они ни находились. На практике часто возникала ситуация, когда новый пользователь, подключившийся к системе IP-TV из Европы, в качестве партнеров получал узлы, расположенные в США. Можно было бы исключить такие ситуации, ограничив круг потенциальных партнеров для каждого нового узла узлами, находящимися недалеко (с точки зрения сетевой задержки) от него. При этом не требовалось бы менять протокол взаимодействия узлов, достаточно только изменить принцип выбора узлов-партнеров. Однако решение этой проблемы не было найдено, так как на практи- ке невозможно измерить сетевую задержку меж- ду всеми узлами, если их десятки или сотни тысяч.
Для решения описанной проблемы предлагается учитывать топологию глобальной компьютерной сети с целью определения узлов, находящихся в одной локальной сети либо в соседних локальных сетях. Для этого каждому узлу должно быть сопоставлено некоторое свойство, определяющее его физическое местонахождение в глобальной компьютерной сети. В качестве такого свойства предлагается использовать маршрут от сервера до узла, который представляет собой множество маршрутизаторов (точнее – их IP-адреса). В этом случае маршруты узлов, находящихся в одной локальной сети, будут совпадать с точностью до последнего маршрутизатора. Маршруты узлов из соседних локальных сетей будут совпадать полностью, за исключением нескольких маршрутизаторов. Фактически уровень совпадения маршрутов от сервера до узлов определяет «близость» этих узлов друг к другу в сетевой инфраструктуре. На основе информации о маршрутах можно так выбирать узлы-партнеры, что средняя задержка между партнерами будет существенно ниже, а скорость обмена трафика между ними повысится в несколько раз по сравнению с используемыми сейчас технологиями. При этом количество процедур получения маршрутов будет равно числу пользователей системы.
Сбор информации о сетевой топологии предлагается проводить с помощью метода трассировки маршрутов, который нашел реализацию в программах traceroute (Linux) и tracert (Windows). Здесь маршрут – это линейно упорядоченное множество объектов компьютерной сети, через которые проходит сетевой пакет на пути следования между двумя узлами компьютерной сети.
На основе данного метода можно найти маршрут (Zs,p) между сервером (s) системы распределения потоков и любым узлом (p). Таким образом, Zs,p={s, r1, …, rk, p}, где R={r1, …, rk} – множество IP-адресов маршрутизаторов компьютерной сети, входящих в этот маршрут. Множество маршрутов Z соответствует графу  (T, E), где T – множество вершин (узлы компьютерной сети), а E – множество дуг (связи между узлами на сетевом уровне). При этом T={si, r1, …, rk, p}, а E={e(si, r1), e(r1, r2), …, e(sk-1, rk), e(rk, p)}. Пример графа, полученного после объединения множества маршрутов, представлен на рисунке 1.
(T, E), где T – множество вершин (узлы компьютерной сети), а E – множество дуг (связи между узлами на сетевом уровне). При этом T={si, r1, …, rk, p}, а E={e(si, r1), e(r1, r2), …, e(sk-1, rk), e(rk, p)}. Пример графа, полученного после объединения множества маршрутов, представлен на рисунке 1.
Полученный таким образом граф (G) обладает несколькими важными свойствами:
– граф G является взвешенным; вес ребра, соединяющего две вершины G, – это сетевая задержка между узлами компьютерной сети, соответствующими этим вершинам;
– граф G является связным, то есть между любыми двумя его вершинами есть путь;
– граф G имеет два типа вершин: vm и vn (vm – маршрутизаторы сети, vn – узлы сети);
– вершины со степенью, равной 1, принадлежат к типу vn;
– вершины со степенью, больше 1, принадлежат к типу vm.
На основе данного графа необходимо провести многоуровневую группировку вершин типа vn.. В результате должно быть получено множество групп Tfin={T1, T2, …, Th}, где Tf – множество вершин vn, у которых f общих вершин типа vm, а fÎ[1, h], то есть T1 – множество групп вершин с одной общей вершиной типа vm, а Th – группа, объединяющая все вершины vn. Пример такой группировки представлен на рисунке 1.
 В идеале группировка должна быть выполнена таким образом, чтобы группы на каждом уровне были одинаковыми по размеру. Поскольку специфика графа G в том, что объединять вершины vn можно только через общую вершину vm, степень которой может быть любой (кроме единицы), такое объединение не всегда достижимо. Поэтому задача алгоритма многоуровневой группировки – объединить вершины vn так, чтобы группы на одном уровне были как можно более близкими по размеру, насколько это позволяет смежность вершин графа.
В идеале группировка должна быть выполнена таким образом, чтобы группы на каждом уровне были одинаковыми по размеру. Поскольку специфика графа G в том, что объединять вершины vn можно только через общую вершину vm, степень которой может быть любой (кроме единицы), такое объединение не всегда достижимо. Поэтому задача алгоритма многоуровневой группировки – объединить вершины vn так, чтобы группы на одном уровне были как можно более близкими по размеру, насколько это позволяет смежность вершин графа.
Анализ современных алгоритмов многоуровневой группировки показал, что на данный момент не существует алгоритма, удовлетворяющего вышеуказанным требованиям, поэтому для решения данной задачи был предложен следующий алгоритм.
Дано: граф G на множестве вершин T={t1, …, tb} и его матрица смежности MG. При этом
– значение MG(i, j) равно сетевой задержке между i-й и j-й вершинами;
– каждый i-й элемент T обладает степенью d(i), которая является степенью соответствующей вершины и равна количеству ненулевых значений в i-й строке матрицы MG;
– каждый i-й элемент T сам является множеством и обладает размером size(i), равным мощности этого множества.
Пример такого графа G представлен на рисунке 2а.
Описание алгоритма.
Шаг 1. Удаляем из G все вершины типа vm , у которых степень равна двум. Удаление происходит по следующему принципу.
Проходим слева направо по всем строкам матрицы MG, тип вершин которых vm. Находим такие строки матрицы i, j1, j2, что MG(i, j1)¹0, MG(i, j2)¹0, а " jxÎ[1, k], jx¹j1, jx¹j2, MG(i, jx)=0. Для каждой тройки i, j1, j2 устанавливаем MG(j1, j2)= MG(i, j1)+MG(i, j2) и MG(j2, j1)=MG(i, j1)+MG(i, j2), а затем удаляем строку и столбец c номером i. Пример полученного графа G после 1-го шага представлен на рисунке 2б.
Шаг 2. Упорядочиваем в  элементы по возрастанию их степени, то есть T={t1, …, tb}, где ti>ti-1, если iÎ[2, b] и d(ti)>d(ti-1).
элементы по возрастанию их степени, то есть T={t1, …, tb}, где ti>ti-1, если iÎ[2, b] и d(ti)>d(ti-1).
Все образовавшиеся подгруппы элементов T с равными степенями сортируем по возрастанию размера этих элементов, то есть " ti " ti-1, если iÎ[2, b] и d(ti)=d(ti-1), то ti>ti-1, если size(ti)>size(ti-1).
Шаг 3. Проходим по T от меньшего элемента к большему и для каждого его i-го элемента выполняем следующие действия с i-й строкой матрицы MG:
1) находим множество номеров столбцов J, такое, что "jÎJ (MG(i, j)¹0);
2) если номер какого-либо столбца j из J соответствует вершине типа «маршрутизатор», считаем, что y=j, и переходим к пункту 6;
3) находим такое множество XÍJ, что "xÎX (d(x)= ), где
), где 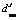 – максимальная степень элементов T с индексами из J;
– максимальная степень элементов T с индексами из J;
4) находим такое множество YÍX, что "yÎY (size(y)= ), где
), где  – минимальный размер элементов T с индексами из X;
– минимальный размер элементов T с индексами из X;
5) находим такой элемент yÎY, что значение MG(i, y) является минимальным;
6) суммируем i-ю и y-ю строки матрицы и записываем результат в i-ю строку; суммируем i-й и y-й столбцы матрицы в один и записываем результат в i-й столбец;
7) устанавливаем MG(i, y)=0 и MG(y, i)=0;
8) удаляем y-й столбец и y-ю строку из матрицы MG;
9) если y-й элемент является маршрутизатором, никаких действий не предпринимаем, в противном случае объединяем y-й элемент списка T с i-м элементом и устанавливаем его на позицию i-го элемента.
Шаг 4. Запоминаем множество T с номером итерации it (в виде Tit) и, если оно состоит более чем из одного элемента, переходим к шагу 2. Если же в ½T½=1, считаем алгоритм завершенным.
В результате работы алгоритма будет получено необходимое упорядоченное множество Tfin={T1, T2, …, Th}, где h – количество итераций, Tit – множество групп узлов it-го уровня.
На рисунке 2а изображен пример графа, для которого необходимо получить множество Tfin. Пример работы алгоритма после 1-го шага представлен на рисунке 2б, после первой итерации – на рисунке 2в, после второй – на рисунке 2г. Результатом работы является множество Tfin={T1, T2, T3}, T1={{1}, {2, 3}, {4, 5, 6}, {7, 8}}, T2={{2, 3}, {4, 5, 6}, {1, 7, 8}}, T3={{2, 3, 4, 5, 6, 1, 7, 8}}.
Полученное множество Tfin дает информацию, на основе которой можно выбрать партнеров по обмену данными для каждого узла пиринговой сети. При этом партнерами могут быть только узлы, находящиеся в одной группе на том или ином уровне. Сервер (узел-источник данных) входит в число узлов. Остается выбрать уровень группировки. Современные пиринговые алгоритмы используют уровень h – выбираются узлы-партнеры из всего доступного множества узлов, то есть сетевая топология не учитывается. Если, например, выбрать уровень 1, то возникнет проблема недоступности данных: данные будут получать только те узлы, которые попали на первом уровне в одну группу с сервером. Поэтому каждому узлу следует выбрать часть узлов из его группы на 1-м уровне, часть из 2-й и т.д. вплоть до уровня h. То есть, если  – группа узла p на уровне it, то множество партнеров узла p (Lp) будет рассчитываться так:
– группа узла p на уровне it, то множество партнеров узла p (Lp) будет рассчитываться так:
 где np – количество партнеров для каждого узла; RAND(X, q) – функция, возвращающая q случайных элементов из множества X;
где np – количество партнеров для каждого узла; RAND(X, q) – функция, возвращающая q случайных элементов из множества X;  – округленное целое значение.
– округленное целое значение.
Оценка эффективности предложенного метода на основе результатов модельного эксперимента
Для подтверждения эффективности предложенного метода был проведен комплекс модельных экспериментов. В качестве критериев эффективности выбраны следующие характеристики:
– производительность (средний битрейт потоков, получаемых пользователями);
– масштабируемость (снижение среднего битрейта при увеличении количества пользователей);
– задержка поступления данных на конечные узлы.
 При проведении эксперимента были реализованы модели функционирования технологий CoolStreaming [2], PPLive [4] и предложенная система выбора партнеров, которая получила название CRSelector (Cluster-Routed Selector). Выбор CoolStreaming и PPLive обусловлен тем, что эти технологии получили широкое распространение на практике и доказали свою экономическую целесообразность.
При проведении эксперимента были реализованы модели функционирования технологий CoolStreaming [2], PPLive [4] и предложенная система выбора партнеров, которая получила название CRSelector (Cluster-Routed Selector). Выбор CoolStreaming и PPLive обусловлен тем, что эти технологии получили широкое распространение на практике и доказали свою экономическую целесообразность.
Для проведения модельного эксперимента использовался написанный на C++ открытый программный пакет OMNeT++, который позволяет построить имитационную модель сети Интернет с реализацией протокола Ethernet, всех протоколов стека TCP/IP и др. [1]. Выбор OMNeT++ обусловлен его популярностью в академической среде исследователей в области телекоммуникаций и открытостью исходного кода. В процессе разработки модели для OMNet++ были добавлены дополнительные програм- мные модули, определяющие порядок функционирования технологий CoolStreaming, PPLive и предложенной методики выбора партнеров CRSelector.
Перед проведением эксперимента были определены следующие характеристики модели Интернет:
– количество маршрутизаторов – 90;
– задержка между маршрутизаторами – случайная величина с нормальным распределением (математическое ожидание – 7,3 мс, дисперсия – 8,9);
– количество интерфейсов у маршрутизаторов, то есть количество физических связей с другими маршрутизаторами, – случайная величина с равномерным распределением в интервале [2, 4].
Выбор данных характеристик был обусловлен проведенным авторами в июне 2009 года исследованием европейского, российского и ближневосточного сегментов Интернета.
При построении моделей CoolStreaming, PPLive и CRSelector были выбраны следующие характеристики:
– количество пользователей – от 10 до 950;
– битрейт медиапотока, передаваемого сервером, – 1500 Кбит/с;
– размер фрагмента потока – 20 Кбайт (160 Кбит);
– количество фрагментов в единицу времени, достаточное для воспроизведения видео без потерь (sconst), – 6 за секунду;
– продолжительность сессии пользователей – от 10 секунд до 60 минут;
– количество партнеров у каждого узла – 10.
 Модельный эксперимент проводился на компьютере со следующими параметрами: процессор – 2 х AMD Opteron 246 2 ГГц, объем оперативной памяти – 2 Гб, операционная система – Linux Debian 4.0.
Модельный эксперимент проводился на компьютере со следующими параметрами: процессор – 2 х AMD Opteron 246 2 ГГц, объем оперативной памяти – 2 Гб, операционная система – Linux Debian 4.0.
Время моделирования (локальное время модели) составило 5 часов.
Из рисунка 3 видно, что использование технологий PPLive и CoolStreaming при величине битрейта, передаваемого сервером, 1500 Кбит/с приводит к тому, что до пользователей доходит только 65 % данных. Использование CRSelector при первоначальном выборе партнеров позволило снизить потери с 35 % до 13 %. Кроме того, на рисунке 4 показано, что использование CRSelector позволяет снизить задержку поступления потока приблизительно в два раза, что является важным преимуществом в случае ведения онлайн-трансляции в прямом эфире. Кроме того, заблаговременное поступление данных снижает уровень их потерь, поскольку в случае потокового вещания данные, передаваемые по сети, актуальны только до определенного момента времени.
Таким образом, в данной статье предложен новый подход к выбору узлов-партнеров пиринговой системы потоковой передачи данных с использованием информации о сетевой топологии. Основные достоинства предложенного метода (CRSelector) в соответствии с результатами модельного эксперимента – независимость от используемой технологии распределения медиапотоков; уве- личение производительности системы: повышение уровня среднего битрейта, поступающего ко- нечным пользователям, на 30 % за счет почти трехкратного снижения потерь; обеспечение достаточного уровня масштабируемости: увеличение среднего битрейта не зависит от количества пользователей. Кроме того, данный метод позволяет снизить среднюю задержку потоков в два раза.
Литература
1. Zhang X., Liu J., Li B., Yum T.-S.P., CoolStreaming/ DONet: A data-driven overlay network for peer-to-peer live media streaming, Proc. IEEE INFOCOM, 2005, Vol. 3, pp. 2102–2111.
2. Biskupski B., Cunningham R., Dowling J., Meier R., High-bandwidth mesh-based overlay multicast in heterogeneous environments, Proc. AAA-IDEA¢06, ACM 2006, no. 4.
3. PPLive. URL: http://pplive.com (дата обращения: 25.12.2012).
4. PPStream. URL: http://ppstream.com, свободный (дата обращения: 25.12.2012).
5. OMNET++ Discrete Event Simulation System. URL: http://www.omnetpp.org/index.php (дата обращения: 20.12.2012).
6. CISCO reports. URL: http://www.cisco.com/en/US/solu tions/collateral/ns341/ns525/ns537/ns705/ns827/white_paper_c11-481360.pdf (дата обращения: 10.11.2012).
7. Тюхтин М.Ф. Системы Интернет-телевидения. М.: Горячая линия–Телеком, 2008. 320 с.
8. Setton E., Girod B., Peer-to-Peer Video Streaming, Springer Science+Business Media, LLC, 2007.
 (T, E), где T – множество вершин (узлы компьютерной сети), а E – множество дуг (связи между узлами на сетевом уровне). При этом T={si, r1, …, rk, p}, а E={e(si, r1), e(r1, r2), …, e(sk-1, rk), e(rk, p)}. Пример графа, полученного после объединения множества маршрутов, представлен на рисунке 1.
(T, E), где T – множество вершин (узлы компьютерной сети), а E – множество дуг (связи между узлами на сетевом уровне). При этом T={si, r1, …, rk, p}, а E={e(si, r1), e(r1, r2), …, e(sk-1, rk), e(rk, p)}. Пример графа, полученного после объединения множества маршрутов, представлен на рисунке 1.
 элементы по возрастанию их степени, то есть T={t1, …, tb}, где ti>ti-1, если iÎ[2, b] и d(ti)>d(ti-1).
элементы по возрастанию их степени, то есть T={t1, …, tb}, где ti>ti-1, если iÎ[2, b] и d(ti)>d(ti-1). ), где
), где 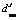 – максимальная степень элементов T с индексами из J;
– максимальная степень элементов T с индексами из J; ), где
), где  – группа узла p на уровне it, то множество партнеров узла p (Lp) будет рассчитываться так:
– группа узла p на уровне it, то множество партнеров узла p (Lp) будет рассчитываться так: где np – количество партнеров для каждого узла; RAND(X, q) – функция, возвращающая q случайных элементов из множества X;
где np – количество партнеров для каждого узла; RAND(X, q) – функция, возвращающая q случайных элементов из множества X;  – округленное целое значение.
– округленное целое значение.

