Моделирование напряженно-деформированного состояния грунтов при циклической нагрузке является одной из главных областей исследования в гражданском строительстве. Решение геотехнических задач все чаще и чаще выполняется с использованием численных методов, в частности, метода конечных элементов. Выбор адекватной упруго-пластической теории здесь является определяющим.
 Упруго-пластические модели, как правило, формулируются в скоростях, используя законы теории пластического течения. Численное интегрирование этих моделей имеет решающее значение для успешного моделирования геотехни- ческих задач. Схема, показывающая место под- программы интегрирования упруго-пластической модели неявным методом Эйлера внутри программы метода конечных элементов, приведена на рисунке 1. Основной целью подпрограммы является вычисление приращений напряжений и параметров упрочнений грунта Ds и Dq. Здесь используются обозначения D=n+1–n, где n+1 и n соответствуют значениям функции, вычисленным в моменты времени tn+1 и tn. Кроме того, подпрограмма вычисляет соответствующие касательные модули грунта
Упруго-пластические модели, как правило, формулируются в скоростях, используя законы теории пластического течения. Численное интегрирование этих моделей имеет решающее значение для успешного моделирования геотехни- ческих задач. Схема, показывающая место под- программы интегрирования упруго-пластической модели неявным методом Эйлера внутри программы метода конечных элементов, приведена на рисунке 1. Основной целью подпрограммы является вычисление приращений напряжений и параметров упрочнений грунта Ds и Dq. Здесь используются обозначения D=n+1–n, где n+1 и n соответствуют значениям функции, вычисленным в моменты времени tn+1 и tn. Кроме того, подпрограмма вычисляет соответствующие касательные модули грунта  , которые будут применяться в последующих итерациях. При использовании касательных модулей нелинейный конечно-элементный алгоритм имеет асимптотическую скорость сходимости, что является одним из ключевых элементов для эффективного геотехнического анализа.
, которые будут применяться в последующих итерациях. При использовании касательных модулей нелинейный конечно-элементный алгоритм имеет асимптотическую скорость сходимости, что является одним из ключевых элементов для эффективного геотехнического анализа.
Для моделирования механического поведения песчаных грунтов наиболее популярной является двухповерхностная модель Дафалиаса и Манзари [1]. Она разработана на основе концепции критических состояний и позволяет описать наблюдаемые в опыте эффекты упрочнения и дилатансии плотных и рыхлых песков.
Согласно модели Дафалиаса–Манзари коэффициент пористости в критическом состоянии грунта определяется уравнением

 где ec, ref – начальное значение критического коэффициента пористости; p – давление; pat – атмосферное давление; lс, x – константы грунта.
где ec, ref – начальное значение критического коэффициента пористости; p – давление; pat – атмосферное давление; lс, x – константы грунта.
Скорость полной деформации упруго-пластического грунта складывается из упругой и пластической частей:  где
где  – соответственно тензоры скоростей полной, упругой и пластической деформации.
– соответственно тензоры скоростей полной, упругой и пластической деформации.
Упругие свойства грунта описываются соотношениями Гука:  где
где  – тензор-девиатор скоростей деформации и скорость объемной деформации;
– тензор-девиатор скоростей деформации и скорость объемной деформации;  – тензор-девиатор скоростей напряжений и скорость среднего напряжения; G, K – модули сдвига и объемной деформации.
– тензор-девиатор скоростей напряжений и скорость среднего напряжения; G, K – модули сдвига и объемной деформации.
Модули G и K определяются выражениями:


где G0 – константа грунта; n – коэффициент Пуассона.
Поверхность текучести задается в форме конуса вращения с уравнением 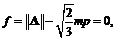 где
где  ; m – угловой коэффициент, принятый константой грунта; a – безразмерный тензор-девиатор, определяющий положение оси конуса в пространстве главных напряжений.
; m – угловой коэффициент, принятый константой грунта; a – безразмерный тензор-девиатор, определяющий положение оси конуса в пространстве главных напряжений.
Принимается неассоциированный закон пластического течения. Нормаль к поверхности текучести  определяется выражением
определяется выражением  где
где  – девиаторная часть тензора, определяющего направление нормали к поверхности текучести в p-плоскости;
– девиаторная часть тензора, определяющего направление нормали к поверхности текучести в p-плоскости;  – тензор второго ранга; dij – символ Кронекера.
– тензор второго ранга; dij – символ Кронекера.
Для учета влияния третьего инварианта тензора напряженного состояния используется функция  где
где  – отношение угловых коэффициентов при растяжении и сжатии; q – угол вида напряженного состояния Лоде.
– отношение угловых коэффициентов при растяжении и сжатии; q – угол вида напряженного состояния Лоде.
Линия, параллельная нормали n, пересекает предельную, критическую и дилатансионную поверхности в трех точках (рис. 2) c соответствующими тензорами кинематического упрочнения грунта: 
где  na – константы грунта;
na – константы грунта;  – параметр упрочнения.
– параметр упрочнения.
Скорости пластической деформации определяются тензором

где 
Коэффициент дилатансии грунта

Изменение Ad зависит от изменения тензора структурной дилатансии z:
 где А0 – константа грунта.
где А0 – константа грунта.
Закон кинематического упрочнения принимается в виде  с функцией
с функцией 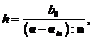 где ain – начальные значения тензора a при инициировании нового процесса нагружения;
где ain – начальные значения тензора a при инициировании нового процесса нагружения; 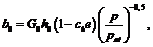 где h0, ch – константы грунта.
где h0, ch – константы грунта.
Закон изменения тензора структурной дилатансии записывается в виде 
 где cz, zmax – константы грунта.
где cz, zmax – константы грунта.
 Численная реализация упруго-пластической модели была выполнена на основе неявного метода Эйлера и итерационной схемы Ньютона–Рафсона [2, 3].
Численная реализация упруго-пластической модели была выполнена на основе неявного метода Эйлера и итерационной схемы Ньютона–Рафсона [2, 3].
Алгоритм получения нелинейного решения заключается в следующем:
1. Задаются начальные значения напряжений и параметров упрочнения: 

2. Проверяются значения функции текучести и невязок: 

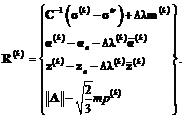
Если  и
и  , то итерации заканчиваются, иначе – переход к п. 3.
, то итерации заканчиваются, иначе – переход к п. 3.
3. Вычисляются приращения напряжений и параметров упрочнения:
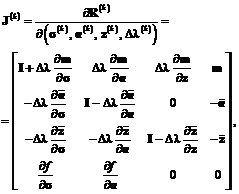


4. Вычисляются новые значения напряжений и параметров упрочнения: 



Далее изменяется номер итерации k←k+1 и выполняется переход к п. 2.
В каждой итерации k уравнения невязки линеаризуются, чтобы найти более близкое решение с  При последующей итерации k+1 значения
При последующей итерации k+1 значения  находятся путем перехода от
находятся путем перехода от  к
к  с использованием упругих модулей
с использованием упругих модулей  , законов пластического течения и упрочнения. Так как поверхность текучести выпуклая, применяемая итерационная схема (рис. 3) гарантирует сходимость решения.
, законов пластического течения и упрочнения. Так как поверхность текучести выпуклая, применяемая итерационная схема (рис. 3) гарантирует сходимость решения.
На основе разработанного алгоритма составлена вычислительная программа для ЭВМ на языке Visual Fortran. Программа апробирована на результатах известных опытов по трехосному сжатию изотропно-уплотненных образцов песчаного грунта в стабилометре [4].
Характеристики грунта, при которых выполнялись расчеты, представлены в таблице, где они разделены на группы в зависимости от описываемых ими свойств [5].
Константы модели
|
Свойство
|
Характеристики
|
|
Упругость
|
G0
|
125
|
|
n
|
0,05
|
|
Критическое состояние
|
M
|
1,25
|
|
c
|
0,712
|
|
ec,ref
|
0,934
|
|
l
|
0,019
|
|
x
|
0,7
|
|
Дилатансия
|
nd
|
2,1
|
|
A0
|
0,704
|
|
nb
|
1,25
|
|
Кинематическое упрочнение
|
h0
|
7,05
|
|
ch
|
0,968
|
|
Структурная дилатансия
|
zmax
|
2,0
|
|
cz
|
600
|
На рисунке 4 приведены расчетные кривые, которые сопоставлены с экспериментальными данными, полученными для песка различной плотности при монотонном нагружении с последующей разгрузкой. Как видим, результаты расчета достоверно описывают поведение грунта.

 На рисунке 5 представлен теоретический прогноз деформации плотного песка при циклическом нагружении с постоянным p. Очевидно, что поведение со значительным разрыхлением будет наблюдаться и для реальных образцов плотного грунта.
На рисунке 5 представлен теоретический прогноз деформации плотного песка при циклическом нагружении с постоянным p. Очевидно, что поведение со значительным разрыхлением будет наблюдаться и для реальных образцов плотного грунта.
Полученные результаты теоретического прогноза напряженно-деформированного состояния песчаных грунтов при монотонном и циклическом нагружении показали эффективность вычислительного алгоритма и позволяют рекомендовать его для конечно-элементных расчетов в геотехническом проектировании.
Литература
1. Dafalias Y.F., Manzari M.T., Journ. of Engineering Mechanics, 2004, no. 130 (6), pp. 622–634.
2. Zienkiewicz O.C., Taylor R.L., The Finite Element Method, Solid Mechanics, Butterworth-Heinemann, 2000, Vol. 24, 59 p.
3. Миронов В.А., Софьин О.Е. Упруговязкопластическое деформирование анизотропных оснований // Вестн. МГСУ, 2011. № 7. С. 570–576.
4. Verdugo R., Ishihara K., Soils and Foundations, 1996, no. 36 (2), pp. 81–91.
5. Taiebat M., Jeremic B., Dafalias Y.F., Kaynia A.M., Cheng Z., Soil Dynamics and Earthquake Engineering, 2010, no. 30, pp. 236–257.
References
1. Dafalias Y.F., Manzari M.T., Journ. of Engineering Me-chanics, 2004, no. 130 (6), pp. 622–634.
2. Zienkiewicz O.C., Taylor R.L., The Finite Element Meth-od, Solid Mechanics, Butterworth-Heinemann, Vol. 24, 2000,
459 p.
3. Mironov V.A., Sofin O.E., Vestnik MGSU [Proc. of Mos-cow State Construction Univ.], no. 7, 2011, pp. 570–576.
4. Verdugo R., Ishihara K., The steady state of sandy soils. Soils and Foundations, 1996, no. 36(2), pp. 81 –91.
5. Taiebat M., Jeremic B., Dafalias Y.F., Kaynia A.M., Cheng Z., Soil Dynamics and Earthquake Engineering, 2010, no. 30, pp. 236–257.

 , которые будут применяться в последующих итерациях. При использовании касательных модулей нелинейный конечно-элементный алгоритм имеет асимптотическую скорость сходимости, что является одним из ключевых элементов для эффективного геотехнического анализа.
, которые будут применяться в последующих итерациях. При использовании касательных модулей нелинейный конечно-элементный алгоритм имеет асимптотическую скорость сходимости, что является одним из ключевых элементов для эффективного геотехнического анализа.
 где ec, ref – начальное значение критического коэффициента пористости; p – давление; pat – атмосферное давление; lс, x – константы грунта.
где ec, ref – начальное значение критического коэффициента пористости; p – давление; pat – атмосферное давление; lс, x – константы грунта. где
где  – соответственно тензоры скоростей полной, упругой и пластической деформации.
– соответственно тензоры скоростей полной, упругой и пластической деформации. где
где  – тензор-девиатор скоростей деформации и скорость объемной деформации;
– тензор-девиатор скоростей деформации и скорость объемной деформации;  – тензор-девиатор скоростей напряжений и скорость среднего напряжения; G, K – модули сдвига и объемной деформации.
– тензор-девиатор скоростей напряжений и скорость среднего напряжения; G, K – модули сдвига и объемной деформации.

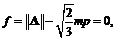 где
где  ; m – угловой коэффициент, принятый константой грунта; a – безразмерный тензор-девиатор, определяющий положение оси конуса в пространстве главных напряжений.
; m – угловой коэффициент, принятый константой грунта; a – безразмерный тензор-девиатор, определяющий положение оси конуса в пространстве главных напряжений. определяется выражением
определяется выражением  где
где  – девиаторная часть тензора, определяющего направление нормали к поверхности текучести в p-плоскости;
– девиаторная часть тензора, определяющего направление нормали к поверхности текучести в p-плоскости;  – тензор второго ранга; dij – символ Кронекера.
– тензор второго ранга; dij – символ Кронекера. где
где  – отношение угловых коэффициентов при растяжении и сжатии; q – угол вида напряженного состояния Лоде.
– отношение угловых коэффициентов при растяжении и сжатии; q – угол вида напряженного состояния Лоде.
 na – константы грунта;
na – константы грунта;  – параметр упрочнения.
– параметр упрочнения.


 где А0 – константа грунта.
где А0 – константа грунта. с функцией
с функцией 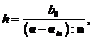 где ain – начальные значения тензора a при инициировании нового процесса нагружения;
где ain – начальные значения тензора a при инициировании нового процесса нагружения; 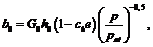 где h0, ch – константы грунта.
где h0, ch – константы грунта.
 где cz, zmax – константы грунта.
где cz, zmax – константы грунта. Численная реализация упруго-пластической модели была выполнена на основе неявного метода Эйлера и итерационной схемы Ньютона–Рафсона [2, 3].
Численная реализация упруго-пластической модели была выполнена на основе неявного метода Эйлера и итерационной схемы Ньютона–Рафсона [2, 3].



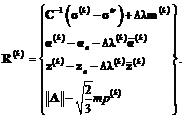
 и
и  , то итерации заканчиваются, иначе – переход к п. 3.
, то итерации заканчиваются, иначе – переход к п. 3.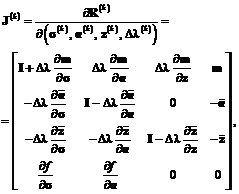






 При последующей итерации k+1 значения
При последующей итерации k+1 значения  находятся путем перехода от
находятся путем перехода от  к
к  с использованием упругих модулей
с использованием упругих модулей  , законов пластического течения и упрочнения. Так как поверхность текучести выпуклая, применяемая итерационная схема (рис. 3) гарантирует сходимость решения.
, законов пластического течения и упрочнения. Так как поверхность текучести выпуклая, применяемая итерационная схема (рис. 3) гарантирует сходимость решения.
 На рисунке 5 представлен теоретический прогноз деформации плотного песка при циклическом нагружении с постоянным p. Очевидно, что поведение со значительным разрыхлением будет наблюдаться и для реальных образцов плотного грунта.
На рисунке 5 представлен теоретический прогноз деформации плотного песка при циклическом нагружении с постоянным p. Очевидно, что поведение со значительным разрыхлением будет наблюдаться и для реальных образцов плотного грунта.