Упругопластическая задача с большими пластическими деформациями физически и геометрически существенно нелинейная [1]. Для ее решения методом конечных элементов требуется значительное количество времени и возникает задача решения системы линейных алгебраических уравнений (СЛАУ) Ax=b с матрицей жесткости A и вектором b правой части относительно искомого вектора x обобщенной скорости в узлах конечно-элементной сетки.
Существенно сократить время вычислений можно с помощью техники с параллельной архитектурой, к которой относятся, в частности, кластерные системы. Построение локальных матриц жесткости в методе конечных элементов может выполняться полностью параллельно, как и пересчет напряженно-деформированного состояния. Однако алгоритмизация распределенного параллельного решения СЛАУ является сложной задачей.
Матрица A имеет ленточный вид с относительно небольшой шириной ленты. Ширина зависит как от типа аппроксимирующей расчетную область сетки, так и от способа нумерации ее узлов и является единственной основной характеристикой матрицы СЛАУ. В данной работе для рассматриваемого алгоритма решения системы уравнений с целью упрощения анализа результатов используются только регулярные сетки с одинаковым числом ячеек d вдоль каждой из сторон. Для таких сеток отношение полуширины ленты b к размерности n вектора x (к количеству переменных в задаче) для двухмерных и трехмерных задач приблизительно одинаково и, например, равно 0,01, 0,005 и 0,0033 для d=100, 200 и 300 соответственно.
В работе [2] была рассмотрена производительность трехдиагонального алгоритма LU-разложения при решении двухмерной упругопластической задачи. Использование его в трехмерной задаче приводит к появлению большого заполнения при вычислении LU-разложения, и алгоритм показывает плохую производительность. В работе [3] описан алгоритм решения СЛАУ с полностью заполненной матрицей с использованием LU-разложения с двухмерным циклическим распределением матрицы по процессорам, а в [4] дано описание модификации данного алгоритма для ленточной матрицы системы. Он базируется на алгоритме блочного LU-разложения [5] с использованием распределения матрицы по процессорам согласно работе [6]. Модификация алгоритма заключается в том, что происходит хранение в памяти лишь тех блоков, в которых могут находиться ненулевые элементы матрицы.
Целью работы является исследование эффективности распределенного параллельного алгоритма решения СЛАУ с двухмерным циклическим распределением матрицы в упругопластической задаче.
Алгоритм параллельного решения СЛАУ
Использование блочной формы хранения позволяет получить меньший объем передачи данных для каждого процессора и большую эффективность использования процессорного кэша [7]. При инициализации алгоритма строится структура данных, хранящая индекс первого столбца блочной строки в массиве блоков, номер столбца первого ненулевого блока и количество ненулевых блоков в строке. В рассматриваемом алгоритме распределение матрицы производится на двухмерную процессорную сетку g=nr´nc с nr и nc, равными соответственно количеству строк и столбцов. Каждый процессор в процессорной сетке должен иметь возможность выполнять массовые операции внутри своей строки или столбца. Это реализовано пользовательскими коммуникаторами MPI [8], в которых находятся только процессоры из конкретного столбца или строки процессорной сетки.
Алгоритм параллельного решения СЛАУ можно разделить на несколько стадий: разбиение матрицы на блоки, нумерация блоков матрицы, перестановка блоков матрицы, формирование локальных частей матрицы, вычисление LU-разложения, решение системы с разложенной матрицей.
Разбиение матрицы на блоки. Матрица разбивается на квадратные блоки размерности nk´nk. При вычислении на платформах x86 и x86_64 компании Intel для достижения большей производительности инструкция по оптимизации [9] рекомендует использовать базовые адреса для массивов, кратные 16, и для типа данных double иметь четное количество элементов в строке при использовании схемы хранения матриц с ведущей строкой. Поэтому использована степень 2 в качестве значений nk.
Нумерация блоков матрицы. Каждому блоку матрицы ставится в соответствие номер nb. Данная нумерация в общем случае может быть произвольной. Кроме этого, каждому блоку матрицы дополнительно по простой схеме циклического распределения [6] присваивается номер процессора np, на котором будут производиться вычисления над этим блоком. Пример разбиения матрицы на блоки и нумерации блоков номерами np показан на рисунке 1. В рамку заключен фрагмент, соответствующий одной процессорной сетке g=2´3.

 Перестановка блоков матрицы. На базе номеров nb и np, полученных на этапе нумерации блоков матрицы, формируется список пар (nb, np). Данные пары на каждом процессоре сортируются по номеру процессора np для объединения блоков матрицы в группы с одинаковыми номерами процессоров np. Далее над массивом блоков выполняется операция перестановки, задаваемая номерами nb из отсортированного списка пар (nb, np). Целью перестановки является создание групп блоков для их пересылки на другие процессоры, номера которых определяются номерами np.
Перестановка блоков матрицы. На базе номеров nb и np, полученных на этапе нумерации блоков матрицы, формируется список пар (nb, np). Данные пары на каждом процессоре сортируются по номеру процессора np для объединения блоков матрицы в группы с одинаковыми номерами процессоров np. Далее над массивом блоков выполняется операция перестановки, задаваемая номерами nb из отсортированного списка пар (nb, np). Целью перестановки является создание групп блоков для их пересылки на другие процессоры, номера которых определяются номерами np.
Формирование локальных частей матрицы. На данном этапе производится пересылка групп блоков, сформированных на предыдущем этапе. Сначала вычисляется количество блоков в каждой из групп, и эти данные передаются процессору с номером np. Затем передаются сами блоки. Для передачи данной информации используется операция MPI_Alltoallv.
Вычисление LU-разложения. После получения процессорами частей матрицы СЛАУ применяется алгоритм блочного LU-разложения. Этот алгоритм является обобщением алгоритма LU-разложения [5]. Пусть матрица СЛАУ A размерности n, кратной nk, разбита на блоки Ai,j размерности nk´nk. Тогда LU-разложение матрицы A вычисляется повторением следующих i-х шагов, i=1, …, m, m=n/nk:
1. вычисляется разложение Ai,i=Li,iUi,i;
2. вычисляются блоки Ui,j матрицы U:
Ui,j=L-1i,iAi,j, j=i+1, …, m;
3. вычисляются блоки Li,j матрицы L:
Li,j=Ai,jU-1i,j, j=i+1, …, m;
4. вычисляется дополнение Шура:
Ãj,k=Aj,k–Lj,iUi,k, j, k=i+1, …, m.
Так как на процессорах хранятся только блоки матрицы A с ненулевыми элементами, i-й шаг алгоритма выполняется с блочной матрицей B наибольшего размера, содержащей только ненулевые блоки, элементом B1,1 которой является блок Ai,i. На рисунке 2 жирными линиями выделена матрица B, у которой блоком B1,1 является блок A2,2.
Сначала вычисляется LU-разложение блока B1,1, которое рассылается процессорам, находящимся в одинаковых столбцах и строках процессорной сетки. Внутри столбца процессорной сетки – блоки матрицы L, а внутри строки процессорной сетки – блоки матрицы U. Полученные блоки матрицы L рассылаются по строкам процессорной сетки, а блоки матрицы U – по столбцам процессорной сетки. После получения необходимых данных каждый процессор вычисляет дополнение Шура для оставшихся блоков матрицы B.
Решение системы с разложенной матрицей. Решение системы состоит из шагов прямой и обратной подстановок. Эти шаги симметричны друг другу с учетом того, что в случае прямой подстановки используется поддиагональная часть Li,i блока, стоящего на главной диагонали матрицы L, а в случае обратной – наддиагональная часть Ui,i матрицы U.
Прямая и обратная подстановки состоят из вычисления произведений Ai,jxj, объединения их результатов на процессоре, имеющем блок Ai,i, и вычисления одной из подстановок с этим блоком:  и
и 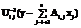 для прямой и обратной подстановок соответственно.
для прямой и обратной подстановок соответственно.
Результаты вычислительных экспериментов
Вычислительные эксперименты проводились на кластере UMT Института математики и механики УрО РАН (г. Екатеринбург). Каждый из 208 вычислительных узлов был оборудован двумя 4-ядерными процессорами Intel Xeon E5450 и 16 ГБ оперативной памяти. Узлы соединены между собой Infiniband для передачи сообщений и Gigabit Ethernet для ввода-вывода. Для компиляции использовался компилятор Intel 11.1 20100414, для передачи сообщений – OpenMPI.
Анализ эффективности применения параллельных вычислений проводился на примере решения методом конечных элементов трехмерной задачи сжатия параллелепипеда и двухмерной задачи сжатия цилиндра плоскими плитами из упругопластического изотропного и изотропно-упрочняемого материала с определяющими соотношениями, полученными в работе [10] и удовлетворяющими закону Гука, ассоциированному закону пластического течения и условию текучести Мизеса с функцией текучести k=400(1+50ep)0.28, где k – напряжение текучести; ep – степень пластической деформации. Решение основано на принципе виртуальной мощности в скоростной форме [1].
Относительно контакта с плитами было принято условие прилипания металла к ним. Нагрузка в виде перемещения плиты прикладывалась малыми шагами Dh. Шаг Dh выбирался таким, чтобы отношение Dh/h (h – высота параллелепипеда или цилиндра) не превышало предел упругости по деформации, в данном случае 0,002, что обеспечивает устойчивость вычислительной процедуры. Величина относительного сжатия параллелепипеда и цилиндра принята равной 0,5.
На каждом шаге нагрузки задача рассматривалась как квазистатическая, а вариационное равенство принципа виртуальной мощности в скоростной форме с помощью конечно-элементной аппроксимации сводилось к СЛАУ.
При распараллеливании формирования глобальной матрицы жесткости конечные элементы распределялись слоями между процессорами. При этом операция объединения матрицы жесткости осуществлялась только с соседними процессорами. При таком распараллеливании количество процессоров не может превышать количество слоев конечных элементов.
Вычислительный эксперимент для задачи сжатия параллелепипеда производился с параметрами, представленными в таблице 1.
Таблица 1
Параметры сеток в вычислительных экспериментах в задаче сжатия параллелепипеда
|
Количество разбиений d
|
Полуширина ленты матрицы СЛАУ b
|
Число неизвестных n
|
k/n
|
|
5
|
131
|
648
|
0,202
|
|
10
|
401
|
3993
|
0,100
|
|
15
|
821
|
12288
|
0,067
|
|
20
|
1391
|
27783
|
0,050
|
|
25
|
2111
|
52728
|
0,040
|
Зависимость ускорения вычисления LU-разложения и решения СЛАУ в упругопластической задаче сжатия параллелепипеда от размера процессорной сетки показана на рисунке 3. Здесь и далее ap=t/t2 – ускорение; t – время, затраченное на вычисление на процессорной сетке размером g=nr´nc; t2 – время, затраченное на вычисление на процессорной сетке размером g=1´2.
 Из рисунке 3а видно, что при увеличении количества процессоров наблюдается ускорение на всех сетках, кроме сетки с числом разбиений d=10. На ней время, затрачиваемое на передачу данных, начинает превышать время, затрачиваемое на вычисления, и наблюдается замедление при использовании 8 процессоров. При вариации неквадратных сеток, то есть замены, например, 1´2 на 2´1 и 2´4 на 4´2, не происходит существенное изменение ускорения. Отсюда можно заключить, что ориентация неквадратных процессорных сеток практически не влияет на производительность LU-разложения. На сетке с количеством разбиений d=25 при увеличении количества процессоров с 2 до 16 происходит ускорение практически в 7 раз, что показывает хорошую масштабируемость алгоритма на данном участке.
Из рисунке 3а видно, что при увеличении количества процессоров наблюдается ускорение на всех сетках, кроме сетки с числом разбиений d=10. На ней время, затрачиваемое на передачу данных, начинает превышать время, затрачиваемое на вычисления, и наблюдается замедление при использовании 8 процессоров. При вариации неквадратных сеток, то есть замены, например, 1´2 на 2´1 и 2´4 на 4´2, не происходит существенное изменение ускорения. Отсюда можно заключить, что ориентация неквадратных процессорных сеток практически не влияет на производительность LU-разложения. На сетке с количеством разбиений d=25 при увеличении количества процессоров с 2 до 16 происходит ускорение практически в 7 раз, что показывает хорошую масштабируемость алгоритма на данном участке.
Из рисунка 3б видно, что производительность алгоритма решения СЛАУ зависит от количества столбцов в процессорной сетке. Зубчатый характер рисунка обусловлен тем, что происходит чередование сеток с большим и меньшим количеством столбцов в процессорной сетке.
Вычислительный эксперимент для двухмерной упругопластической задачи сжатия цилиндра выполнялся с параметрами, представленными в таблице 2.
Таблица 2
Параметры сеток в вычислительных экспериментах в задаче сжатия цилиндра
|
Количество разбиений d
|
Полуширина ленты матрицы СЛАУ b
|
Число неизвестных n
|
k/n
|
|
100
|
205
|
20402
|
0,0100
|
|
200
|
405
|
80802
|
0,0050
|
|
300
|
605
|
181202
|
0,0033
|
Зависимость ускорения при вычислении LU-разложения и решении СЛАУ в этой задаче показана на рисунке 4.
Из него видно, что при увеличении количества разбиений d увеличивается ускорение при вычислении как LU-разложения, так и решения СЛАУ. Полуширина матриц в двухмерной задаче невелика (см. табл. 2), и при увеличении процессорной сетки требуется уменьшать размеры блоков и локальных частей матрицы. В экстремальных точках графиков ускорений имеет место преобладание времени, затрачиваемого на передачу данных, над временем, затрачиваемым на вычисления. Падение всех линий графика для решения СЛАУ (см. рис. 4б) определяется тем, что на процессорной сетке 2´2 появляется передача данных внутри столбцов сетки.
В трехмерной задаче полуширина ленты матрицы больше, чем в двухмерном случае, поэтому на рассмотренных процессорных сетках выигрыш по времени от использования большего количества процессоров превышает временные затраты на межпроцессорное взаимодействие. Так как количество элементов в матрице жесткости трехмерной задачи растет гораздо быстрее, чем в двухмерной, и ширина ленты матрицы жесткости получается больше, чем в случае двухмерной задачи, рассматриваемый алгоритм показывает лучшие результаты в трехмерном случае.
Использова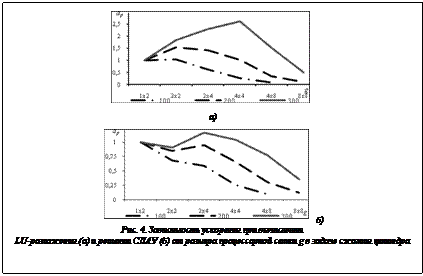 ние большого количества процессоров в трехмерной задаче было ограничено выбранным распределением конечных элементов по процессорам слоями. Если для двухмерной задачи это было оправдано тем, что количество элементов в слое сравнительно небольшое, то в трехмерной задаче в слое находится большое количество конечных элементов, а число самих слоев невелико. Так как количество начальных ненулевых элементов в строке матрицы жесткости не зависит от числа конечных элементов, в дальнейшем представляется целесообразным использовать разряженные схемы хранения матрицы и подобный подход к распараллеливанию этапа построения матрицы жесткости. Это позволит более гибко распределять конечные элементы между процессорами.
ние большого количества процессоров в трехмерной задаче было ограничено выбранным распределением конечных элементов по процессорам слоями. Если для двухмерной задачи это было оправдано тем, что количество элементов в слое сравнительно небольшое, то в трехмерной задаче в слое находится большое количество конечных элементов, а число самих слоев невелико. Так как количество начальных ненулевых элементов в строке матрицы жесткости не зависит от числа конечных элементов, в дальнейшем представляется целесообразным использовать разряженные схемы хранения матрицы и подобный подход к распараллеливанию этапа построения матрицы жесткости. Это позволит более гибко распределять конечные элементы между процессорами.
На основании изложенного можно сделать следующие выводы. При решении СЛАУ в трехмерной упругопластической задаче алгоритм LU-разложения с двухмерным циклическим распределением матрицы показал рост производительности с увеличением числа процессоров. В двухмерной задаче алгоритм показал рост производительности лишь на процессорных сетках меньше 4´4. Это было обусловлено небольшим размером полуширины ленты матрицы жесткости, из-за чего пересылка блоков между процессорами занимала больше времени, чем вычисления над блоками.
Литература
1. Поздеев A.А., Трусов П.В., Няшин Ю.И. Большие упругопластические деформации. М.: Наука, 1986. 232 с.
2. Коновалов А.В., Толмачев А.В., Партин А.С. Параллельное решение упругопластической задачи с применением трехдиагонального алгоритма LU-разложения из библиотеки SCALAPACK // Вычислительная механика сплошных сред. 2011. Т. 4. № 4. С. 34–41. URL: http://www.icmm.ru/journal/ download/CCMv4n4a4.pdf.
3. Choi J., Dongarra J.J., Ostrouchov S., Petitet A.P., Walker D.W., Whaley R.C., The Design and Implementation of the ScaLAPACK LU, QR, and Cholesky Factorization Routines. Sc. Progr., 1996, pp. 173–184.
4. Walker D.W., Aldcroft T., Cisneros A., Fox G.C., Furmanski W., LU decomposition of banded matrices and the solution of linear systems on hypercubes. In Proceedings of the third conference on Hypercube concurrent computers and applications, ACM, NY, USA, 1989, Vol. 2, pp. 1635–1655.
5. Watkins D.S., Fundamentals of Matrix Computations. 2nd ed. John Wiley and Sons, 2002, 618 p.
6. Hendrickson B.A., Womble D.E., The Torus-Wrap Mapping For Dense Matrix Calculations On Massively Parallel Computers, SIAM J. Sci. Stat. Comput., 1994, Vol. 15, pp. 1201–1226.
7. Lam M.S., Rothberg E.E., Wolf M.E., The Cache Performance and Optimization of Blocked Algorithms. Proc. 4th Intern. Conf. on Architectural Support for Programming Languages and Operating Systems, 1991, pp. 63–74.
8. MPI: A Message-Passing Interface Standard Version 2.2. URL: http://www.mpi-forum.org/docs/mpi-2.2/mpi22-report.pdf (дата обращения: 12.11.2012).
9. Intel® 64 and IA-32 Architectures Optimization Reference Manual. URL: http://www.intel.com/content/www/us/en/architecture-and-technology/64-ia-32-architectures-optimization-manual.html (дата обращения: 12.11.2012).
10. Konovalov A.V., Constitutive relations for an elastoplastic medium under large plastic deformations. Mechanics of Solids, 1997, Vol. 32, no. 5, pp. 117–124.
References
1. Pozdeev A.A., Trusov P.V., Nyashin Yu.I., Bolshie uprugo-plasticheskie deformatsii [Big elasto-plastic deformations], Moscow, Nauka, 1986.
2. Konovalov A.V., Tolmachev A.V., Partin A.S., Computational Continuum Mechanics, 2011, Vol. 4, no. 4, pp. 34–41, available at: http://www.icmm.ru/journal/download/CCMv4n4a4.pdf (accessed 21 April 2013).
3. Choi J., Dongarra J.J., Ostrouchov S., Petitet A.P., Walker D.W., Whaley R.C., Scientific Programming, 1996, pp. 173–184.
4. Walker D.W., Aldcroft T., Cisneros A., Fox G.C., Furmanski W., Proc. of the 3rd conf. on Hypercube concurrent computers and applications, Vol. 2. ACM, 1989, NY, USA, pp. 1635–1655.
5. Watkins D.S., Fundamentals of Matrix Computations, 2nd ed., John Wiley and Sons, 2002.
6. Hendrickson B.A., Womble D.E., SIAM Journ. on Stat. Computing, 1994, Vol. 15, pp. 1201–1226.
7. Lam M.S., Rothberg E.E., Wolf M.E., Proc. of the 4th Int. Conf. on Architectural Support for Programming Languages and Operating Systems, 1991, pp. 63–74.
8. MPI: A Message-Passing Interface Standard Version 2.2, available at: http://www.mpi-forum.org/docs/mpi-2.2/mpi22-report. pdf (accessed 12 November 2012).
9. Intel® 64 and IA-32 Architectures Optimization Reference Manual, available at: http://www.intel.com/content/www/us/en/architecture-and-technology/64-ia-32-architectures-optimization-manual.html (accessed 12 November 2012).
10. Konovalov A.V., Mechanics of Solids, 1997, Vol. 32, no. 5, pp. 117–124.


 и
и 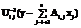 для прямой и обратной подстановок соответственно.
для прямой и обратной подстановок соответственно. Из рисунке 3а видно, что при увеличении количества процессоров наблюдается ускорение на всех сетках, кроме сетки с числом разбиений d=10. На ней время, затрачиваемое на передачу данных, начинает превышать время, затрачиваемое на вычисления, и наблюдается замедление при использовании 8 процессоров. При вариации неквадратных сеток, то есть замены, например, 1´2 на 2´1 и 2´4 на 4´2, не происходит существенное изменение ускорения. Отсюда можно заключить, что ориентация неквадратных процессорных сеток практически не влияет на производительность LU-разложения. На сетке с количеством разбиений d=25 при увеличении количества процессоров с 2 до 16 происходит ускорение практически в 7 раз, что показывает хорошую масштабируемость алгоритма на данном участке.
Из рисунке 3а видно, что при увеличении количества процессоров наблюдается ускорение на всех сетках, кроме сетки с числом разбиений d=10. На ней время, затрачиваемое на передачу данных, начинает превышать время, затрачиваемое на вычисления, и наблюдается замедление при использовании 8 процессоров. При вариации неквадратных сеток, то есть замены, например, 1´2 на 2´1 и 2´4 на 4´2, не происходит существенное изменение ускорения. Отсюда можно заключить, что ориентация неквадратных процессорных сеток практически не влияет на производительность LU-разложения. На сетке с количеством разбиений d=25 при увеличении количества процессоров с 2 до 16 происходит ускорение практически в 7 раз, что показывает хорошую масштабируемость алгоритма на данном участке. ние большого количества процессоров в трехмерной задаче было ограничено выбранным распределением конечных элементов по процессорам слоями. Если для двухмерной задачи это было оправдано тем, что количество элементов в слое сравнительно небольшое, то в трехмерной задаче в слое находится большое количество конечных элементов, а число самих слоев невелико. Так как количество начальных ненулевых элементов в строке матрицы жесткости не зависит от числа конечных элементов, в дальнейшем представляется целесообразным использовать разряженные схемы хранения матрицы и подобный подход к распараллеливанию этапа построения матрицы жесткости. Это позволит более гибко распределять конечные элементы между процессорами.
ние большого количества процессоров в трехмерной задаче было ограничено выбранным распределением конечных элементов по процессорам слоями. Если для двухмерной задачи это было оправдано тем, что количество элементов в слое сравнительно небольшое, то в трехмерной задаче в слое находится большое количество конечных элементов, а число самих слоев невелико. Так как количество начальных ненулевых элементов в строке матрицы жесткости не зависит от числа конечных элементов, в дальнейшем представляется целесообразным использовать разряженные схемы хранения матрицы и подобный подход к распараллеливанию этапа построения матрицы жесткости. Это позволит более гибко распределять конечные элементы между процессорами.