Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Author: () - | |
| Ключевое слово: |
|
| Page views: 13504 |
Print version Full issue in PDF (2.31Mb) |
В 1985 году Нил Коблиц и Виктор Миллер независимо предложили использовать эллиптические кривые для криптосистем с открытым ключом. Со второй половины 90-х годов криптосистемы на эллиптических кривых стали приобретать важное практическое значение. Эффективность криптосистем на эллиптических кривых зависит от эффективности алгоритмов умножения скаляра на точку. Задача умножения скаляра на точку состоит в вычислении следующей суммы:
Метод Коблица-Солинаса, используемый для поля характеристики два, на сегодняшний день является самым быстрым методом для умножения скаляра на точку (см., например: J.A. Solinas. Efficient Arithmetic on Koblitz curves. 2000). Последние несколько лет наблюдается интерес к методам быстрого умножения скаляра на точку в полях характеристики три (Nigel P. Smart, E.J. Westwood. Point Multiplication on Ordinary Elliptic Curves over Fields of Characteristic Three. 2003). Это связано с появлением нового направления эллиптической криптографии – криптосистем, основанных на билинейных отображениях. Данная работа посвящена модификации метода Коблица-Солинаса для поля характеристики три. На основе известных алгоритмов предложен новый алгоритм умножения скаляра на точку. Арифметика эллиптических кривых, заданных над полем характеристики три Рассмотрим неособую кривую над полем
где Арифметические операции на кривой (1) могут быть определены следующим образом. Сложение точек:
Удвоение точек:
В таблице 1 приведены оценки сложности операций, выраженные через сложность полевых операций, где M – сложность умножения; I – сложность нахождения обратного. Таблица 1
Прямая модификация метода Коблица-Солинаса Пусть E – это эллиптическая кривая вида (1), определенная над конечным полем Можно проверить, что кривая, заданная в поле характеристики три будет удовлетворять следующему свойству:
для каждой точки Определим отображение Тогда (2) можно переписать как
Решение уравнения (3): Скаляр k может быть представлен как ряд Найдем правило для нахождения ряда по основанию Теорема: Доказательство. Поскольку из (3) мы можем найти, что Отметим, что Для того чтобы снизить длину последовательности в работе Майера и Штэфельбаха, было отмечено, что Если k выбран около Для иллюстрации алгоритма деления возьмем кривую Его корень Для нахождения алгоритма деления Алгоритм 1. Вычисление Вход: Выход:
return Рассмотрим алгоритм 2, на входе котрого будет комплексное число Алгоритм 2. Тернарное знаковое представление Вход: Выход: Тернарное знаковое представление по основанию
repeat
if end if
untill return Если Алгоритм 3. Вычисление Вход: Выход: Использовать алгоритм 1 для нахождения Использовать алгоритм 2 для нахождения
for
If
end if if
end if end for return Средняя сложность алгоритма составит Использование метода разбиения для прямой модификации метода Коблица-Солинаса Разобьем ряд по основанию
Обозначим
Главное свойство полученной последовательности (4) состоит в том, что длина последовательности уменьшается наполовину. Алгоритм 3 использует разбиение при вычислении Алгоритм 4. Метод разбиения. Вход: Выход: Использовать алгоритм 1 для нахождения Использовать алгоритм 2 для нахождения If
end if
Предвычислим:
for
return Средняя сложность алгоритма составит Таблица 2 содержит оценки сложности изложенных ранее методов с предложенным (A – стоимость сложения двух точек; Таблица 2
Очевидно, что при выборе |
| Permanent link: http://swsys.ru/index.php?id=369&lang=en&page=article |
Print version Full issue in PDF (2.31Mb) |
| The article was published in issue no. № 3, 2007 |
Perhaps, you might be interested in the following articles of similar topics:
- Место XML-технологий в среде современных информационных технологий
- К вопросу параметризации свойств программных средств обучения
- Информационная поддежка технического обеспечения кораблей при первой операции флота
- Новый подход к проблеме коллективного выбора на базе удовлетворения взаимных требований сторон
- Оценка защищенности информации от несанкционированного доступа при помощи имитационной модели системы защиты информации
Back to the list of articles
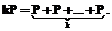
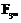 :
: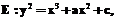 (1)
(1)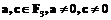 .
.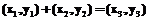 :
: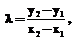
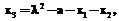
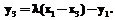
 :
:
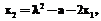
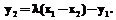

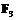 . Поскольку кривая определена над
. Поскольку кривая определена над 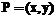 – точка на кривой E, то точка
– точка на кривой E, то точка 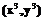 будет так же лежать на кривой E.
будет так же лежать на кривой E.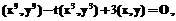 (2)
(2)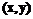 на E, где
на E, где 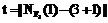 , где
, где 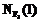 – колличество
– колличество 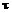 :
: 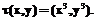
 . (3)
. (3)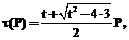 где
где 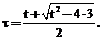
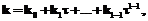
 , и затем
, и затем 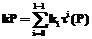 , применяя правило Горнера,
, применяя правило Горнера, 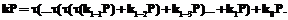
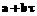 делится на
делится на 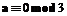 .
.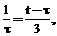 тогда
тогда 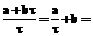
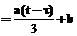 . Последнее выражение делится на 3 тогда и только тогда, когда
. Последнее выражение делится на 3 тогда и только тогда, когда 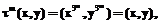 тогда
тогда 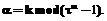
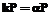 (см.: W. Meier, O. Staffelbach. Efficient Multiplication on Certain Nonsupersingular Elliptic Curves. 1992).
(см.: W. Meier, O. Staffelbach. Efficient Multiplication on Certain Nonsupersingular Elliptic Curves. 1992).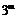 , то длина знакового тернарного представления по основанию
, то длина знакового тернарного представления по основанию 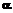 вычислим, чему равно
вычислим, чему равно 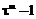 в виде
в виде 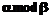 . Первая задача может быть решена с применением следующей рекурсивной процедуры. Пусть
. Первая задача может быть решена с применением следующей рекурсивной процедуры. Пусть 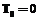 ,
,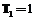 и
и 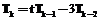 для
для 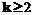 . Легко видеть, что
. Легко видеть, что 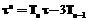 .
.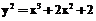 c
c 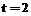 . Характеристическое уравнение будет иметь следующий вид:
. Характеристическое уравнение будет иметь следующий вид: 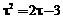 .
.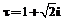 .
.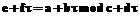 найдем сопряженное к
найдем сопряженное к 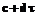 . Сопряженное будет
. Сопряженное будет 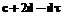 . Умножим числитель и знаменатель
. Умножим числитель и знаменатель 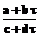 на
на 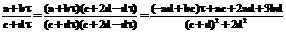 .
.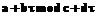 .
.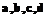
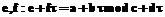
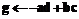
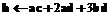
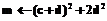
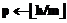
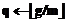
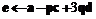
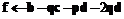
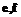
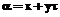 , а на выходе – последовательность коэффициентов
, а на выходе – последовательность коэффициентов 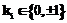 , таких что
, таких что 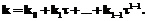
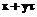 по основанию
по основанию 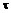 .
.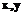 ,t
,t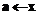 ,
,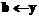
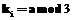 ,
, 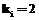 then
then 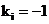
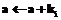
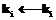
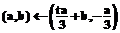
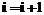
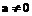 and
and 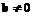
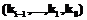
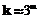 , тогда длина ряда по основанию
, тогда длина ряда по основанию 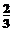 .
.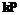 .
.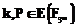
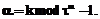
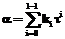
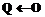
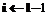 ,
,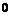 do
do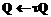
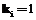 then
then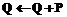
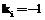 then
then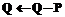
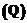
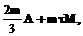 где A – сложность сложения;
где A – сложность сложения; 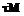 – сложность вычисления отображения
– сложность вычисления отображения 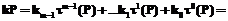
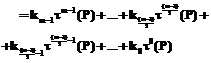
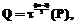 тогда
тогда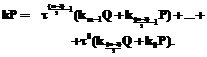 (4)
(4)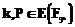
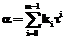
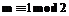 then
then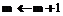
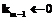
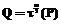
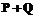 ,
,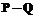 ,
,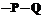 ,
,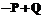
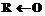
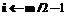 ,
,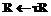

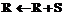
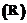
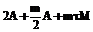 .
.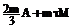

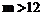 использование метода разбиения по сравнению с прямой модификацией метода Коблица-Солинаса будет давать выигрыш.
использование метода разбиения по сравнению с прямой модификацией метода Коблица-Солинаса будет давать выигрыш.