Классической задачей теории вероятностей является задача определения вероятности произведения (совместного появления) событий, рассчитываемой на основании теоремы умножения вероятностей и следствий из нее. При этом результирующую вероятность можно рассчитать лишь при наличии сведений о вероятностях перемножаемых событий (безусловных для независимых, условных для зависимых). В простейших случаях их значения могут быть определены из теоретических соображений либо на основании статистических наблюдений, тогда их величина выражается не имеющим единицы измерения действительным числом от нуля до единицы включительно. Однако подобная информация о вероятностях тех или иных событий доступна не всегда, и приходится использовать экспертные оценки, выражающиеся, в соответствии с особенностями человеческого мышления и речи, понятиями «высокий», «очень низкий» и т.п. Понятия такого рода формализуются нечеткими числами в рамках теории нечетких множеств, предложенной Л. Заде в 1965 г. Область применения данного математического аппарата достаточно широкая, и в последнее время его популярность растет. Это обусловлено тем, что в любой системе с социальной составляющей вполне естественной является именно нечеткая оценка как достигнутого уровня развития, так и перспектив системы. Неопределенность условий реализации человеческих усилий особенно высока, если дело касается получения результатов интеллектуальной деятельности. Планируя развитие производства, например, путем внедрения инновационных продуктов и способов производства [1], необходимо располагать информацией об использовании подобных инноваций другими хозяйствующими субъектами, о неточности и/или неполноте имеющихся данных, о приближенных оценках фактического экономического эффекта от внедрения и т.п. Методы, используемые для обоснования решений, должны учитывать эту неопределенность уже на этапе разработки инноваций. Однако чистый вероятностный подход можно использовать только на поздних стадиях распространения нововведения, когда накоплено достаточное количество статистических данных о результатах его использования: лишь на их основании удается идентифицировать распределения вероятностей и их параметры. Отсутствие подобных статистических данных на ранних стадиях приводит к неопределенности невероятностного типа, успешно описываемой в рамках теории нечетких множеств. Использование такого метода оправдано также в других социально-экономических системах [2]. Математические методы теории нечетких множеств зачастую проще, чем их аналоги в теории вероятностей [3], точнее отражают действительность, позволяют математически оперировать понятиями, близкими к естественному языку ЛПР.
Однако в ряде случаев при программной реализации методов нечеткой математики возникают определенные трудности. Так, при определении вероятности наступления конкретного исхода в задаче о приобретении инновации предприятием [4], когда вероятности выбора разными участниками конфликта возможных стратегий имеют различную (как четкую, так и нечеткую) природу, возникает необходимость определения произведения четких и нечетких вероятностей, а также представления результата в пригодной для восприятия и интерпретации форме. Поскольку работа с нечеткими числами достаточно трудоемка, практическое решение поставленной задачи предполагает только программную реализацию с использованием ЭВМ.
 Предположим, что множество возможных значений перемножаемых нечетких вероятностей задается пятиуровневым классификатором вида PF= ={pf1=”низкая”; pf2=”довольно низкая”; pf3=”средняя”; pf4=”довольно высокая”; pf5=”высокая”}, причем значение pfi,
Предположим, что множество возможных значений перемножаемых нечетких вероятностей задается пятиуровневым классификатором вида PF= ={pf1=”низкая”; pf2=”довольно низкая”; pf3=”средняя”; pf4=”довольно высокая”; pf5=”высокая”}, причем значение pfi,  является нечетким числом и входит в произведение bi раз,
является нечетким числом и входит в произведение bi раз,  . Естественно считать носителем каждого значения вероятности отрезок [0; 1] и описывать каждое из них нечетким числом вида
. Естественно считать носителем каждого значения вероятности отрезок [0; 1] и описывать каждое из них нечетким числом вида  , где
, где  – функция принадлежности (ФП) вероятности pfi. Наиболее часто используется треугольная ФП (рис. 1), которую в случае пятиуровневого классификатора вероятности и носителя [0; 1] можно определить следующим образом:
– функция принадлежности (ФП) вероятности pfi. Наиболее часто используется треугольная ФП (рис. 1), которую в случае пятиуровневого классификатора вероятности и носителя [0; 1] можно определить следующим образом:
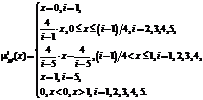 (1)
(1)
Обозначим входящие в произведение четкие сомножители prjÎ[0; 1],  , тогда общий вид искомого произведения можно определить так:
, тогда общий вид искомого произведения можно определить так:
 (2)
(2)
а общее число сомножителей составит  . Понятно, что
. Понятно, что  представляет собой произведение m действительных чисел от нуля до единицы включительно, результатом которого является действительное число. Тогда задача нахождения значения (2) предполагает выполнение трех арифметических операций с нечеткими числами: возведение нечеткого числа в заданную степень, перемножение нечетких чисел и умножение нечеткого числа на четкое число. В методологическом плане задача выполнения перечисленных операций достаточно давно решена в рамках нечеткой арифметики, причем существуют различные способы их определения. Первый возможный подход – на основании принципа расширения, предложенный самим Л. Заде [2]. Второй – в терминах интервальной арифметики (с использованием a-уровней), предложенный в [5] и используемый, например, в [6–8]. Третий – принцип обратных функций, рассмотренный на примере треугольных нечетких чисел в [9]. Четвертый подход – с использованием вероятностных функций и плотностей распределения для произвольных нечетких чисел с непрерывными правым и левым фронтами ФП – предложен в [10]. При этом ни совместное выполнение этих операций, ни случай более двух сомножителей не рассматриваются, что и определяет актуальность данной работы.
представляет собой произведение m действительных чисел от нуля до единицы включительно, результатом которого является действительное число. Тогда задача нахождения значения (2) предполагает выполнение трех арифметических операций с нечеткими числами: возведение нечеткого числа в заданную степень, перемножение нечетких чисел и умножение нечеткого числа на четкое число. В методологическом плане задача выполнения перечисленных операций достаточно давно решена в рамках нечеткой арифметики, причем существуют различные способы их определения. Первый возможный подход – на основании принципа расширения, предложенный самим Л. Заде [2]. Второй – в терминах интервальной арифметики (с использованием a-уровней), предложенный в [5] и используемый, например, в [6–8]. Третий – принцип обратных функций, рассмотренный на примере треугольных нечетких чисел в [9]. Четвертый подход – с использованием вероятностных функций и плотностей распределения для произвольных нечетких чисел с непрерывными правым и левым фронтами ФП – предложен в [10]. При этом ни совместное выполнение этих операций, ни случай более двух сомножителей не рассматриваются, что и определяет актуальность данной работы.
 Наиболее удобным и часто применяемым на практике методом является использование a-уровней (сечений), то есть набора значений принадлежностей, для каждого из которых определены два крайних значения x, таких, что m(x)=a [11]. Тогда каждое нечеткое число может быть представлено в виде конечного множества троек вида
Наиболее удобным и часто применяемым на практике методом является использование a-уровней (сечений), то есть набора значений принадлежностей, для каждого из которых определены два крайних значения x, таких, что m(x)=a [11]. Тогда каждое нечеткое число может быть представлено в виде конечного множества троек вида 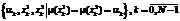 , где N – число a-уровней (рис. 2), а искомые операции над нечеткими числами с треугольными ФП (1) определяются на каждом выбранном уровне a следующим образом.
, где N – число a-уровней (рис. 2), а искомые операции над нечеткими числами с треугольными ФП (1) определяются на каждом выбранном уровне a следующим образом.
1. Возведение нечеткого числа в степень b:

 . (3)
. (3)
2. Произведение степеней bi и bq двух нечетких чисел:
 (4)
(4)
3. Произведение степени bi нечеткого числа и четкого числа PR:
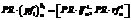 . (5)
. (5)
В соответствии с теоремой Дюбуа и Прейда [12] результатом каждой из перечисленных операций является нечеткое число, следовательно, (2) также будет нечетким числом. Приведение его к четкости (дефаззификация) может быть выполнено, в частности, с использованием метода нахождения абсциссы центра тяжести плоской фигуры, ограниченной результирующей ФП [13], по формуле
 (6)
(6)
При заданном разбиении нечеткого числа по a-уровням переход в (6) к численному интегрированию по формуле трапеций [14] дает выражение для приближенного вычисления искомого значения в виде
 (7)
(7)
Таким образом, алгоритм вычисления произведения (2) предполагает следующие действия.
1. Анализ перемножаемых вероятностей с группировкой четких сомножителей и подсчетом частот каждого из нечетких с представлением результата в виде (2).
2. Перемножение четких чисел с получением единственного четкого множителя.
3. Выбор шага разбиения по a-уровням и вычисление их количества.
4. Возведение каждого из нечетких сомножителей в соответствующую ему степень по формуле (3).
5. Последовательное умножение полученных на шаге 4 степеней нечетких чисел по формуле (4).
6. Умножение полученного на шаге 5 нечеткого числа на вычисленное на шаге 2 четкое число по формуле (5).
7. Приведение полученного на шаге 6 нечеткого результата к четкости по формуле (7).
Алгоритм реализован в среде Borland Delphi 6. Входными данными для программы являются выбранные из списков нечеткие и введенные пользователем вручную четкие значения вероятностей, а также шаг разбиения на a-уровни. Вывод нечеткого результата осуществляется с использованием компонента-диаграммы Chart, а его приведенного к четкости аналога – в Memo-поле. Один из возможных наборов исходных данных и результат работы приложения представлены на рисунке 3.

Таким образом, программная реализация предложенного алгоритма нахождения произведения четких и нечетких вероятностей позволяет успешно определять как нечеткое, так и четкое значения выражения (2). Результат в графической форме позволяет получить наглядное представление о виде ФП результирующей нечеткой вероятности, а ее дефаззифицированный эквивалент (после нормировки в случае необходимости) может быть использован в качестве оценки вероятности конкретного исхода конфликта, в том числе для программной поддержки принятия решений о приобретении инновационной продукции.
Литература
1. Копотева А.В., Затонский А.В. Методы принятия решения о приобретении конкурентоспособной инновационной продукции // Современная наука. Актуальные проблемы теории и практики. 2013. № 3–4. С. 8–16.
2. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. М.: Мир, 1976. 165 с.
3. Беллман Р., Заде Л. Принятие решений в расплывчатых условиях // Вопросы анализа и процедуры принятия решений. М.: Мир, 1976. C. 172–215.
4. Копотева А.В. Поддержка принятия решения о внедрении промышленного инновационного проекта // Новый университет. Технические науки. 2013. № 02. C. 11–15.
5. Kaufmann A., Gupta M.M. Introducing to Fuzzy Arithmetic: Theory and Application. Van Nostrand Reinhold, NY, 1991, 351 p.
6. Chu T.-C., Lin Y. An extension to fuzzy MCDM. Computers and Mathematics with Applications, 2009, no. 57, pp. 445–454.
7. Chen S.-J., Chen S.-M. Fuzzy risk analysis based on measures of similarity between interval-valued fuzzy numbers. Computers and Mathematics with Applications, 2008, no. 55, pp. 1670–1685.
8. Chang P.-T., Chang C.-H. An elaborative unit cost structure-based fuzzy economic production quantity model. Mathematical and Computer Modelling, 2006, no. 43, pp. 1337–1356.
9. Chou Ch.-Ch. The Canonical Representation of Multiplication Operation on Triangular Fuzzy Numbers. Computers and Mathematics with Applications, 2003, no. 45, pp. 1601–1610.
10. Mahantal S., Chutia R., Baruah H.K. Fuzzy Arithmetic without Using the Method of a-cuts. Intern. Journ. of Latest Trends in Computing, Dec. 2010, vol. 1, iss. 2, pp. 73–80.
11. Птускин А.С. Решение стратегических задач в условиях размытой информации: монография. М.: Дашков и Ко, 2003. 240 с.
12. Рутковская Д., Пилиньский Н., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы; [пер. с польск. И.Д. Рудинского]. М.: Горячая линия–Телеком, 2006. 452 с.
13. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления (в 3-х т.). М.: Физматлит, 2006. Т. 2. 864 с.
14. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: БИНОМ. Лаборатория знаний, 2007. 636 с.
References
1. Kopoteva A.V., Zatonskiy A.V. Decision-making methods to get competitive innovative products. Sovremennaya nauka. Aktualnye problemy teorii i praktiki [Modern science: actual problems of theory and practice]. Nauchnye Tekhnologii Publ., 2013, no. 3–4, pp. 8–16 (in Russ.).
2. Zadeh L.A. The concept of a linguistic variable and its application to approximate reasoning. 1973, ERL Publ., 171 p. (Russ. ed.: Moscow, Mir Publ., 1976, 165 p.).
3. Bellman R.E., Zadeh L.A. Decision making in a fuzzy environment. Management Science. 1970, vol. 17, no. 4, pp. B141–B164 (Russ. ed.: Moscow, Mir Publ., 1976, pp. 172–215).
4. Kopoteva A.V. Decision-making support concerning implementation of industrial innovative project. Novy universitet. Tekhnicheskie nauki [The New University. Technical Sciences Series]. 2013, no. 02, pp. 11–15 (in Russ.).
5. Kaufmann A., Gupta M.M. Introducing to Fuzzy Arithmetic: Theory and Application. Van Nostrand Reinhold Publ., NY, 1991, 351 p.
6. Chu T.-C., Lin Y. An extension to fuzzy MCDM. Compu- ters and Mathematics with Applications. 2009, no. 57, pp. 445–454.
7. Chen S.-J., Chen S.-M. Fuzzy risk analysis based on measures of similarity between interval-valued fuzzy numbers. Computers and Mathematics with Applications. 2008, no. 55, pp. 1670–1685.
8. Chang P.-T., Chang C.-H. An elaborative unit cost structure-based fuzzy economic production quantity model. Mathematical and Computer Modelling. 2006, no. 43, pp. 1337–1356.
9. Chou Ch.-Ch. The canonical representation of multiplication operation on triangular fuzzy numbers. Computers and Mathematics with Applications. 2003, no. 45, pp. 1601–1610.
10. Mahantal S., Chutia R., Baruah H.K. Fuzzy arithmetic without using the method of a-cuts. Int. Journ. of Latest Trends in Computing. 2010, vol. 1, iss. 2, pp. 73–80.
11. Ptuskin A.S. Reshenie strategicheskikh zadach v usloviyakh razmytoy informatsii [Strategic tasks solving under fuzzy data conditions]. Monograph, Moscow, “Dashkov i Ko” Publ., 2003, 240 p.
12. Rutkovskaya D., Pilinskiy N., Rutkovskiy L. Neural networks, genetic algorithms and indistinct systems (Russ. ed.: Rudinskiy I.D., Moscow, Goryachaya liniya–Telekom Publ., 2006, 452 p.).
13. Fikhtengolts G.M. Kurs differentsialnogo i integralnogo ischisleniya [A Course of Differential and Integral Calculus]. 2006, Moscow, Fizmatlit Publ., vol. 2, 864 p.
14. Bahvalov N.S., Zhidkov N.P., Kobelkov G.M. Chislennye metody [Numerical computing]. Moscow, BINOM. Laboratorija znaniy Publ., 2007, 636 p.
 Предположим, что множество возможных значений перемножаемых нечетких вероятностей задается пятиуровневым классификатором вида PF= ={pf1=”низкая”; pf2=”довольно низкая”; pf3=”средняя”; pf4=”довольно высокая”; pf5=”высокая”}, причем значение pfi,
Предположим, что множество возможных значений перемножаемых нечетких вероятностей задается пятиуровневым классификатором вида PF= ={pf1=”низкая”; pf2=”довольно низкая”; pf3=”средняя”; pf4=”довольно высокая”; pf5=”высокая”}, причем значение pfi,  является нечетким числом и входит в произведение bi раз,
является нечетким числом и входит в произведение bi раз,  . Естественно считать носителем каждого значения вероятности отрезок [0; 1] и описывать каждое из них нечетким числом вида
. Естественно считать носителем каждого значения вероятности отрезок [0; 1] и описывать каждое из них нечетким числом вида  , где
, где  – функция принадлежности (ФП) вероятности pfi. Наиболее часто используется треугольная ФП (рис. 1), которую в случае пятиуровневого классификатора вероятности и носителя [0; 1] можно определить следующим образом:
– функция принадлежности (ФП) вероятности pfi. Наиболее часто используется треугольная ФП (рис. 1), которую в случае пятиуровневого классификатора вероятности и носителя [0; 1] можно определить следующим образом: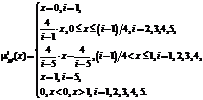 (1)
(1) , тогда общий вид искомого произведения можно определить так:
, тогда общий вид искомого произведения можно определить так: (2)
(2) . Понятно, что
. Понятно, что  представляет собой произведение m действительных чисел от нуля до единицы включительно, результатом которого является действительное число. Тогда задача нахождения значения (2) предполагает выполнение трех арифметических операций с нечеткими числами: возведение нечеткого числа в заданную степень, перемножение нечетких чисел и умножение нечеткого числа на четкое число. В методологическом плане задача выполнения перечисленных операций достаточно давно решена в рамках нечеткой арифметики, причем существуют различные способы их определения. Первый возможный подход – на основании принципа расширения, предложенный самим Л. Заде [2]. Второй – в терминах интервальной арифметики (с использованием a-уровней), предложенный в [5] и используемый, например, в [6–8]. Третий – принцип обратных функций, рассмотренный на примере треугольных нечетких чисел в [9]. Четвертый подход – с использованием вероятностных функций и плотностей распределения для произвольных нечетких чисел с непрерывными правым и левым фронтами ФП – предложен в [10]. При этом ни совместное выполнение этих операций, ни случай более двух сомножителей не рассматриваются, что и определяет актуальность данной работы.
представляет собой произведение m действительных чисел от нуля до единицы включительно, результатом которого является действительное число. Тогда задача нахождения значения (2) предполагает выполнение трех арифметических операций с нечеткими числами: возведение нечеткого числа в заданную степень, перемножение нечетких чисел и умножение нечеткого числа на четкое число. В методологическом плане задача выполнения перечисленных операций достаточно давно решена в рамках нечеткой арифметики, причем существуют различные способы их определения. Первый возможный подход – на основании принципа расширения, предложенный самим Л. Заде [2]. Второй – в терминах интервальной арифметики (с использованием a-уровней), предложенный в [5] и используемый, например, в [6–8]. Третий – принцип обратных функций, рассмотренный на примере треугольных нечетких чисел в [9]. Четвертый подход – с использованием вероятностных функций и плотностей распределения для произвольных нечетких чисел с непрерывными правым и левым фронтами ФП – предложен в [10]. При этом ни совместное выполнение этих операций, ни случай более двух сомножителей не рассматриваются, что и определяет актуальность данной работы.
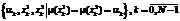 , где N – число a-уровней (рис. 2), а искомые операции над нечеткими числами с треугольными ФП (1) определяются на каждом выбранном уровне a следующим образом.
, где N – число a-уровней (рис. 2), а искомые операции над нечеткими числами с треугольными ФП (1) определяются на каждом выбранном уровне a следующим образом.
 . (3)
. (3) (4)
(4)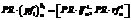 . (5)
. (5) (6)
(6) (7)
(7)
