При решении задач динамики упругих стержневых систем, образованных из стержней сплошного сечения (брус), применяется гипотеза плоских сечений: сечение до и после деформации остается плоским. В матрицах масс балочных конечных элементов (КЭ), используемых в конечно-элементных моделях стержневых систем, инерция кручения стержня обычно не учитывается [1, 2]. В реальных конструкциях стержневых систем, как правило, используются стержни открытого профиля призматической формы: большинство прокатных профилей, а также составных и гнутых профилей, то есть используются тонкостенные стержни. В отличие от обычных стержней сечения тонкостенного стержня при его деформации не остаются плоскими, что исключает возможность использования при расчете тонкостенных стержней гипотезы плоских сечений. В соответствии с теорией тонкостенных стержней В.З. Власова при кручении тонкостенного стержня вследствие депланации  сечения перемещения в направлении продольной оси X стержня изменяются согласно закону секториальных координат (площадей). Это приводит к уравнению равновесия бимоментов в узле, справедливому только для плоских рам, образованных из стержней с симметричным сечением и с узловыми соединениями, у которых депланация концов всех сходящихся стержней одна и та же.
сечения перемещения в направлении продольной оси X стержня изменяются согласно закону секториальных координат (площадей). Это приводит к уравнению равновесия бимоментов в узле, справедливому только для плоских рам, образованных из стержней с симметричным сечением и с узловыми соединениями, у которых депланация концов всех сходящихся стержней одна и та же.
В общем случае пространственные колебания тонкостенного стержня открытого профиля с недеформируемым контуром поперечного сечения описываются следующими дифференциальными уравнениями:
 (1)
(1)
где точками обозначено дифференцирование компонент вектора перемещений по времени; E, G – модули упругости и сдвига материала; Jx, Jy, Jz, Jw – момент инерции чистого кручения, осевые и секториальный моменты инерции сечения соответственно; r – плотность материала стержня; F – площадь сечения; ay, az – координаты центра изгиба (кручения) сечения; r2 – геометрическая характеристика сечения стержня, имеющая линейную размерность:  .
.
Изгибная форма колебаний тонкостенного стержня становится невозможной: в каждое уравнение входят линейные перемещения z, y и углы закручивания jx сечения, то есть система дифференциальных уравнений характеризует взаимодействие изгиба в двух плоскостях и кручения вокруг оси стержня, и в общем случае обе формы зависят друг от друга.
В работе [3] рассмотрена задача пространственных колебаний тонкостенного стержня, при решении которой используют принцип Даламбера, то есть рассматривается статическая задача с добавлением сил инерции масс. Масса и жесткость стержня по длине принимаются постоянными. Приведена модель матрицы порядка 12 масс (продольные перемещения пренебрегаются), состоящая из восьмеричных чисел, каждому из которых соответствует инерционный коэффициент.
Рассмотрим тонкостенный стержневой КЭ с одной осью Y симметрии сечения, который включает кручение стержня вокруг продольной оси X и изгиб в плоскости X–Z. Эксцентриситет осей сечения КЭ по оси симметрии Y и равен ay. Система уравнений (1) распадается на независимый изгиб в плоскости X–Y (1-е уравнение) и уравнения, характеризующие взаимодействие изгиба в плоскости X – Z и кручение:
 (2)
(2)
В соответствии с работой [3] вариация потенциальной энергии деформации стержня равна работе его узловых сил {Pr} на возможных узловых перемещениях d{Zr}. Умножим уравнения (2), характеризующие изгибно-крутильные колебания, на dz, djx:
 (3)
(3)
 .
.
Интегрирование уравнения (3) по частям приводит к следующему выражению:
 (4)
(4)

Величины, характеризующие линейные w и угловые jx перемещения, должны удовлетворять граничным условиям в каждом узле тонкостенного стержня на сами переменные w, jx и на их производные w¢, j¢x. Аналогичные условия в плоском изгибе, в связи с этим
 ;
;
 , (5)
, (5)
где {N} – вектор функций формы поля перемещений в том же виде, что и при изгибе стержня.
Подставив выражения (5) в (4) и выполнив дифференцирование по каждой степени свободы, окончательно получим 
В отличие от [3] в матрице [Kr] жесткости тонкостенного стержневого КЭ, работающего на изгиб и кручение, использована секториальная жесткость EJw сечения, а не жесткость GJx при кручении:


 ,
,
где k – изгибно-крутильная характеристика тонкостенного стержня:  ; m – безразмерный коэффициент искажаемости контура сечения стержня замкнутого профиля (m=1 для сечения стержня открытого профиля).
; m – безразмерный коэффициент искажаемости контура сечения стержня замкнутого профиля (m=1 для сечения стержня открытого профиля).
Матрица жесткости пространственного тонкостенного стержневого КЭ приведена в работе [4].
Инерционные коэффициенты позволили сформировать в явной форме матрицу [Mr] масс тонкостенного стержневого КЭ, работающего на изгиб и кручение, в соответствии с приведенной выше принятой последовательностью и положительными направлениями узловых сил и перемещений:
 ,(6)
,(6)
где K1–K16 – коэффициенты, учитывающие инерцию кручения КЭ:













 ,
,







Используя матрицу (6), можно сформировать матрицу порядка 14 масс пространственного тонкостенного стержневого КЭ с эксцентриситетами осей сечения ay и az:  , где
, где
 ,
,
 ,
,
 .
.
Для сечения с двумя осями симметрии система уравнений (1) распадается на три независимых уравнения:

где первые два характеризуют изгибную форму колебаний в плоскостях X–Z и X–Y соответственно, а третье – чисто крутильную форму колебаний. Решение задачи свободных колебаний тонкостенного стержня позволяет определить минимальную частоту из этих трех форм колебаний.
Решение задач динамики стержневой системы методом конечных элементов реализовано в специализированных программах, разработанных автором и зарегистрированных в Реестре программ для ЭВМ (свид. №№ 2012619735 и 2012619736), ориентированных на решение частных, то есть объектно-ориентированных задач, что позволило построить эффективный вычислительный алгоритм при простоте и минимуме исходных данных.
Общая характеристика программ: ЭВМ – IBM PC-совместимый ПК; язык – Fortran; ОС – Windows; объем – 21,0 Kб и 25,4 Kб исходного текста соответственно.
Программы предназначены для вычисления частот и форм свободных колебаний и амплитудных значений напряженно-деформированного состояния при вынужденных колебаниях с использованием в конечно-элементной модели стержневой системы пространственных балочных и (или) тонкостенных стержневых КЭ. Данные программы обеспечивают выполнение следующих функций:
– расчет стержневой системы, образованной из стержней сплошного сечения и (или) тонкостенных стержней открытого или замкнутого профиля;
– расчет с распределенной массой КЭ и (или) с учетом сосредоточенных масс;
– учет произвольных шарниров в местной и (или) в общей системах координат.
Численная реализация задач динамики стержневой системы выполнена в стандартной конечно-элементной постановке [1, 4]. Предлагаемые программы имеют некоторые особенности реализации.
Минимум исходной информации и простота ее подготовки обеспечиваются одинаковым количеством степеней свободы в узлах модели стерж-невой системы. В связи с этим при совместном использовании балочных и тонкостенных стержневых КЭ в программах предусмотрена модификация матриц жесткости балочных КЭ: в матрицу жесткости вводятся фиктивные (недостающие 7-я и 14-я) степени свободы, соответствующие депланации сечения, путем присваивания нуля всем элементам матрицы соответствующей строки и столбца. При решении разрешающей системы уравнений выполняется проверка матрицы коэффициентов при неизвестных на наличие таких уравнений (0=0) по нулевым элементам на главной диагонали. Проще не исключать эти уравнения, а элементам главной диагонали присвоить числа, отличные от нуля. В результате решения системы уравнений соответствующие перемещения будут равны нулю.
Учет произвольных шарниров выполняется процедурой конденсации (редуцирования) как для матриц жесткости, так и для матриц масс. Для матриц масс данная процедура приближенная, но достаточно точная [4].
В отличие от [1] при анализе свободных колебаний используется следующий подход к формированию системы линейных уравнений вычисления характеристической матрицы [H]: [ ][H]= =[
][H]= =[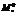 ], где [
], где [ ] – матрица коэффициентов системы уравнений равновесия; [
] – матрица коэффициентов системы уравнений равновесия; [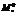 ] – матрица свободных членов.
] – матрица свободных членов.
Решение системы уравнений обеспечивается не исключением зависимых уравнений в матрицах [K0] и [M0] жесткости и масс конструкции, соответствующих условиям кинематического закрепления задачи [1], а связями, накладываемыми на узловые перемещения. Этот способ заключается в том, что размер матриц [K0] и [M0] не изменяется, а сами матрицы модифицируются путем присваивания строкам и столбцам, соответствующим кинематическим закреплениям задачи, нулевых значений, а компоненту главной диагонали – единицы. В результате получим матрицы [ ], [
], [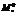 ]. Нулевые строки характеристической матрицы [H] не участвуют в итерационном процессе определения собственных значений, но это обстоятельство должно быть предусмотрено в соответствующей подпрограмме. Однако при исключении зависимых уравнений можно использовать практически все стандартные программы определения собственных значений.
]. Нулевые строки характеристической матрицы [H] не участвуют в итерационном процессе определения собственных значений, но это обстоятельство должно быть предусмотрено в соответствующей подпрограмме. Однако при исключении зависимых уравнений можно использовать практически все стандартные программы определения собственных значений.
В программах предусмотрено формирование матриц масс КЭ как с учетом инерции растяжения-сжатия, так и без учета, путем присваивания соответствующим элементам нулевых значений. Так, расчет балки с заделкой концов с учетом инерции растяжения-сжатия приводит к большим ошибкам округления вычислений, так как продольная жесткость стержня значительно больше изгибной.
Аналогично в матрице жесткости тонкостенного стержня жесткостные характеристики, соответствующие кручению, значительно больше изгибных. Точность вычислений можно повысить, если решать разрешающую систему уравнений равновесия с двойной точностью. Предлагается алгоритм преобразования (развертывания) элементов матрицы из обычной точности в 4 байта в двойную в 8 байт, при котором обе матрицы с обычной FMG и двойной точностью DFMG совпадают. Преобразование выполняется с использованием файла прямого доступа внешней памяти ЭВМ и заключается в следующем.
 В подпрограмме преобразования каждая запись во внешней памяти преобразуется в две записи, каждая из которых той же длины, но каждому элементу матрицы отводится по 8 байт. В цикле 1 четным элементам массива FMG присваиваются нули. В цикле 2 по числу записей KNY из внешней памяти из файла прямого доступа считывается последняя запись, элементы которой присваиваются нечетным элементам массива FMG (рис. 1).
В подпрограмме преобразования каждая запись во внешней памяти преобразуется в две записи, каждая из которых той же длины, но каждому элементу матрицы отводится по 8 байт. В цикле 1 четным элементам массива FMG присваиваются нули. В цикле 2 по числу записей KNY из внешней памяти из файла прямого доступа считывается последняя запись, элементы которой присваиваются нечетным элементам массива FMG (рис. 1).
Очевидно, преобразование элементов матрицы в двойную точность необходимо выполнять снизу. Длина преобразованного таким образом массива FMG увеличивается вдвое, в связи с чем увеличивается вдвое и число записей в файле. На рисун- ке 1 длина одной записи равна шести (в качестве примера).
Единицы измерения силы и длины могут быть выбраны расчетчиком и определяются соответствующими единицами измерения модуля упругости материала.
По программе, созданной автором, выполнены сравнительные расчеты на свободные колебания П-образной рамы, образованной стержнями из швеллера № 12 (F=13,3 см2; Jx=3,63 см4; Jy=304,00 см4; Jz=31,20 см4; Jw=768,30 см6; ay=3,02 см), и рамы, образованной стержнями из двутавра № 12 (F=14,70 см2 ; Jx =4,24 см4; Jy =350,00 см4; Jz =27,90 см4; Jw=1353,00 см6; ay =0) со сторонами по 3 м с использованием балочных КЭ, то есть без учета инерции кручения стержней, и тонкостенных стержневых КЭ при изгибно-крутильной форме колебаний (рис. 2).
 По программе, разработанной автором, выполнены расчеты рам на вынужденные колебания. Основные результаты сравнительных расчетов вариантов рам приведены в таблице, где нормальные напряжения в верхней полке сечения профиля у заделки рамы в узле 1 определены при вынужденных колебаниях рам с частотой w=10 с-1 возмущающей силы в 1 kH, приложенной в узле 7.
По программе, разработанной автором, выполнены расчеты рам на вынужденные колебания. Основные результаты сравнительных расчетов вариантов рам приведены в таблице, где нормальные напряжения в верхней полке сечения профиля у заделки рамы в узле 1 определены при вынужденных колебаниях рам с частотой w=10 с-1 возмущающей силы в 1 kH, приложенной в узле 7.
Моделирование рамы тонкостенными стержневыми КЭ приводит к уменьшению значений частот свободных колебаний и увеличению значений нормальных напряжений при вынужденных колебаниях в сравнении с моделированием рамы балочными КЭ без учета инерции кручения.
 При анализе колебаний плоско-пространственной тонкостенной стержневой системы с использованием тонкостенных стержневых КЭ рассматриваются взаимодействие изгиба в двух плоскостях и кручение вокруг оси стержня, что полнее отражает более сложные моды упругих колебаний, нежели простые моды изгиба из плоскости стержневой системы.
При анализе колебаний плоско-пространственной тонкостенной стержневой системы с использованием тонкостенных стержневых КЭ рассматриваются взаимодействие изгиба в двух плоскостях и кручение вокруг оси стержня, что полнее отражает более сложные моды упругих колебаний, нежели простые моды изгиба из плоскости стержневой системы.
Следует отметить, что неплоскую тонкостенную раму можно рассматривать как плоскую только в том случае, если наибольший вертикальный эксцентриситет в узле рамы не превосходит половину высоты наименьшего из элементов, а наибольший горизонтальный эксцентриситет не превышает удвоенную толщину стенки наименьшего из элементов, сходящихся в узле.
Теории расчета в полной мере удовлетворяют и пространственные тонкостенные стержневые системы, у которых стержни, образующие узел сопряжения, расположены в одной плоскости. На практике на этапе поверочных расчетов произвольной пространственной тонкостенной стержневой системы часто пользуются так называемой технической теорией тонкостенных стержней, основанной на гипотезах о недеформируемости контура поперечного сечения, то есть использовании- ем балочных КЭ в расчетной схеме. При точном расчете пространственная стержневая система рассматривается как оболочка.
Литература
1. Мяченков В.И., Мальцев В.П., Майборода В.П. [и др.]. Расчеты машиностроительных конструкций методом конечных элементов: справочник. М.: Машиностроение, 1989. 520 с.
2. Чернявский А.О. Метод конечных элементов. Основы практического применения. М.: Машиностроение, 2007. 106 с.
3. Иванов А.А. Исследование напряженно-деформированного состояния рам из тонкостенных стержней методом конечных элементов (Применительно к рамам автомобилей и полуприцепов), дис. … канд. техн. наук. 1973. 160 с.
4. Чернов С.А., Дьяков И.Ф. К расчету пространственной тонкостенной стержневой системы // Автоматизация и современные технологии. 2008. № 2. С. 3–7.
5. Голованов А.П., Тюленева О.Н., Шигабутдинов А.Ф. Метод конечных элементов в статике и динамике тонкостенных конструкций. М.: Физматлит, 2006. 392 с.
References
1. Myachenkov V.I., Maltsev V.P., Mayboroda V.P. [et al.]. Raschety mashinostroitelnykh konstruktsiy metodom konechnykh elementov [Calculating engineering constructions using the finite element method]. Guide. Moscow, Mashinostroenie Publ., 1989, 520 p.
2. Chernyavskiy A.O. Metod konechnykh elementov. Osnovy prakticheskogo primeneniya [The finite element method. Practical using]. Moscow, Mashinostroenie Publ., 2007, 106 p.
3. Ivanov A.A. Issledovanie napryazhenno-deformirovannogo sostoyanija ram iz tonkostennykh sterzhney metodom konechnykh elementov (Primenitelno k ramam avtomobiley i polupritsepov) [The research of stressed-deformed state of thin-walled rod frameworks using the finite element method (applying to car and semitrailer frameworks)]. PhD thesis, Leningrad, 1973, 160 p.
4. Chernov S.A., Dyakov I.F. Calculation of the spatial thin-walled rod system. Avtomatizatsiya i sovremennye tekhnologii [Automation and modern technologies]. Mashinostroenie Publ., 2008, no. 2, pp. 3–7 (in Russ.).
5. Golovanov A.P., Tyuleneva O.N., Shigabutdinov A.F. Metod konechnykh elementov v statike i dinamike tonkostennykh konstruktsiy [The finite element method in statics and dynamicks of thin-walled frameworks]. Moscow, Fizmatlit Publ., 2006, 392 p.
 сечения перемещения в направлении продольной оси X стержня изменяются согласно закону секториальных координат (площадей). Это приводит к уравнению равновесия бимоментов в узле, справедливому только для плоских рам, образованных из стержней с симметричным сечением и с узловыми соединениями, у которых депланация концов всех сходящихся стержней одна и та же.
сечения перемещения в направлении продольной оси X стержня изменяются согласно закону секториальных координат (площадей). Это приводит к уравнению равновесия бимоментов в узле, справедливому только для плоских рам, образованных из стержней с симметричным сечением и с узловыми соединениями, у которых депланация концов всех сходящихся стержней одна и та же. (1)
(1) .
.  (2)
(2) (3)
(3) .
. (4)
(4)
 ;
; , (5)
, (5)


 ,
, ; m – безразмерный коэффициент искажаемости контура сечения стержня замкнутого профиля (m=1 для сечения стержня открытого профиля).
; m – безразмерный коэффициент искажаемости контура сечения стержня замкнутого профиля (m=1 для сечения стержня открытого профиля). ,(6)
,(6)












 ,
,






 , где
, где ,
, ,
, .
.
 ][H]= =[
][H]= =[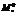 ], где [
], где [

 При анализе колебаний плоско-пространственной тонкостенной стержневой системы с использованием тонкостенных стержневых КЭ рассматриваются взаимодействие изгиба в двух плоскостях и кручение вокруг оси стержня, что полнее отражает более сложные моды упругих колебаний, нежели простые моды изгиба из плоскости стержневой системы.
При анализе колебаний плоско-пространственной тонкостенной стержневой системы с использованием тонкостенных стержневых КЭ рассматриваются взаимодействие изгиба в двух плоскостях и кручение вокруг оси стержня, что полнее отражает более сложные моды упругих колебаний, нежели простые моды изгиба из плоскости стержневой системы.