Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: (Konstantin.Zingerman@tversu.ru) - , Ph.D, () - | |
| Ключевое слово: |
|
| Page views: 8925 |
Print version Full issue in PDF (1.17Mb) |
Методика приближенного аналитического решения плоских задач имеет следующий вид. Методом малого параметра решение задачи сводится к последовательному решению ряда линеаризованных граничных задач. Алгоритм представлен на примере сжимаемого материала, случая плоской деформации. Введем следующие обозначения: u – вектор перемещений; f – вектор массовых сил; Q – вектор поверхностных сил; N – нормаль; S – тензор напряжений. Введем в рассмотрение комплексные переменные Обозначим через
Уравнения и граничные условия линеаризованной задачи могут быть записаны в комплексной форме следующим образом:
Решение линеаризованной краевой задачи отыскивается в виде:
где
Решение линеаризованной краевой задачи для однородной системы уравнений может быть найдено с помощью комплексных потенциалов Колосова-Мусхелишвили
Рассмотрим случай, когда конечная область, занимаемая телом, конформно отображается на бесконечную область, ограниченную единичной окружностью с центром в начале координат. Граничные условия и вектор поверхностной силы на
Функция
Таким образом, в области, ограниченной единичной окружностью, граничные условия примут вид:
Коэффициенты Изложенный алгоритм реализован в специализированном программном комплексе «Наложение», предназначенном для решения задач теории наложения больших деформаций. |
| Permanent link: http://swsys.ru/index.php?id=388&lang=en&page=article |
Print version Full issue in PDF (1.17Mb) |
| The article was published in issue no. № 2, 2007 |
Perhaps, you might be interested in the following articles of similar topics:
- Оптимизация структуры базы данных информационной системы ПАТЕНТ
- Нейроподобная сеть для решения задачи оптимизации антенной решетки
- Оценка защищенности информации от несанкционированного доступа при помощи имитационной модели системы защиты информации
- Сравнение сложных программных систем по критерию функциональной полноты
- Средства обеспечения надежности функционирования информационных систем
Back to the list of articles
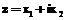 ,
, 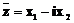 и функции этих переменных
и функции этих переменных 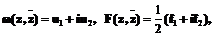

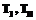 следующие комбинации компонент (в декартовой системе координат) некоторого тензора Т второго ранга:
следующие комбинации компонент (в декартовой системе координат) некоторого тензора Т второго ранга: .
.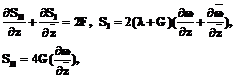
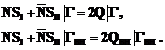
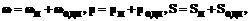
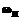 ,
, 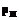 ,
, 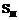 – некоторое частное решение линеаризованной задачи,
– некоторое частное решение линеаризованной задачи,  ,
, 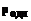 ,
,  – решение линеаризованной задачи для однородной системы уравнений. Частное решение может быть найдено по формулам:
– решение линеаризованной задачи для однородной системы уравнений. Частное решение может быть найдено по формулам: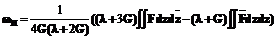 ,
,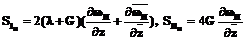 .
.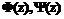 . Выражения для напряжений и комплексного вектора перемещений через комплексные потенциалы имеют вид:
. Выражения для напряжений и комплексного вектора перемещений через комплексные потенциалы имеют вид: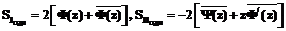 ,
,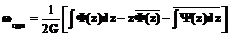 .
.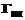 :
: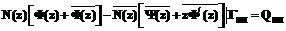 ,
,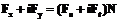 ,
,  ,
,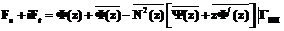 .
.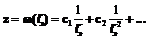 определяет конформное отображение. Комплексные потенциалы имеют следующий вид:
определяет конформное отображение. Комплексные потенциалы имеют следующий вид: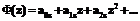 ,
, 
 ,
,  .
.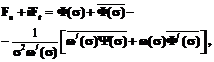

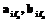 и
и  находятся решением системы линейных уравнений, полученной из граничных условий. Далее находится тензор напряжений S и вектор перемещений u. Таким образом, линеаризованная задача решена.
находятся решением системы линейных уравнений, полученной из граничных условий. Далее находится тензор напряжений S и вектор перемещений u. Таким образом, линеаризованная задача решена.