Генерирование случайных процессов с заданными вероятностной и спектральной мерами является одной из наиболее сложных задач стохастического моделирования [1]. Данное утверждение справедливо для всех законов распределения вероятностей, за исключением нормального распределения, для которого задача моделирования достаточно просто решается для произвольных спектральных мер [2]. До настоящего времени в арсенале исследователей отсутствуют универсальные методы, позволяющие решать эту задачу без существенных ограничений на вид спектральной или вероятностной меры. Тем не менее, в работе [3] был предложен метод, обладающий достаточной универсальностью по отношению к маргинальному закону распределения вероятностей и автокорреляционной функции (АКФ) моделируемого стохастического процесса. Несмотря на столь значимое достоинство, этот метод не получил широкого распространения в силу ряда причин. Основной причиной, ограничивающей его распространение, является отсутствие исследований точности моделирования АКФ.
В силу особенностей метод обладает специфическим видом погрешности моделирования АКФ. Эта погрешность является методической и носит систематический характер, а значение погрешности зависит, как это будет показано далее, от множества параметров алгоритма моделирования. Механизм возникновения погрешности описан авторами метода [3], но каких-либо детальных исследований до сих пор не было проведено.
В данной работе описываются разработка метода оценки точности воспроизведения (моделирования) заданной АКФ методом перестановок [3] и получение первоначальных сведений о свойствах методической погрешности.
Прежде рассмотрим вариант реализации метода, разработанного авторами этой статьи (рис. 1).
 Ведущий процесс, вектор Pm на рисунке 1, формируется на основе линейного динамического преобразования формирователем F1. Закон распределения элементов вектора Pm как таковой значения не имеет, поскольку основной задачей ведущего процесса является формирование заданной АКФ, но точность моделирования зависит от того, как соотносятся законы распределения векторов Pm и Ps. Максимальная точность будет достигнута при выполнении условия совпадения законов распределения P(Pm) = P(Ps). Формирователь F1 представляет собой линейный фильтр, структура и параметры которого однозначно определяются на основании вида АКФ и значений ее параметров. Методы расчетов таких фильтров известны и подробно описаны, например, в [4].
Ведущий процесс, вектор Pm на рисунке 1, формируется на основе линейного динамического преобразования формирователем F1. Закон распределения элементов вектора Pm как таковой значения не имеет, поскольку основной задачей ведущего процесса является формирование заданной АКФ, но точность моделирования зависит от того, как соотносятся законы распределения векторов Pm и Ps. Максимальная точность будет достигнута при выполнении условия совпадения законов распределения P(Pm) = P(Ps). Формирователь F1 представляет собой линейный фильтр, структура и параметры которого однозначно определяются на основании вида АКФ и значений ее параметров. Методы расчетов таких фильтров известны и подробно описаны, например, в [4].
Ведомый процесс, вектор Ps², формируется с заданным одномерным законом распределения. Как правило, эта процедура состоит из этапа формирования вектора с равномерным распределением с последующим его нелинейным преобразованием. На рисунке 1 приведена схема с нелинейным преобразованием, хотя в ряде случаев эта схема может изменяться, например для распределения Симпсона. Формирователь F2 может быть реализован нелинейной функцией или несколькими шагами алгоритма. Существующие методы позволяют в точности воспроизводить заданные одномерные законы распределения [5].
Следующий этап в рассматриваемом методе – ранжирование, то есть расположение элементов векторов Pm и Ps² в порядке возрастания. Для ведомого процесса результатом операции ранжирования является преобразованный вектор Ps¢, для ведущего – вектор перестановок sm.
Заключительный этап метода – операция перестановки: на основании имеющегося вектора sm производится перестановка элементов вектора Ps¢:  .
.
Таким образом, после завершения полного цикла моделирования можно вычислить оценки АКФ для вектора выходного процесса Ps и вектора ведущего процесса Pm. Введем обозначения для этих векторов оценок нормированной АКФ соответственно  и
и  Кроме того, для оценки погрешности доступны и истинные значения требуемой АКФ в виде функции rt(t) от корреляционного сдвига t, на основании которой рассчитываются параметры формирователя F1 (рис. 1). Дискретные значения этой нормированной АКФ обозначим через вектор rt. В дальнейшем посредством r(t) будем обозначать нормированную АКФ, то есть rx(t) = Rx(t)/s2x и rx(0) = 1, где s2x – дисперсия случайного процесса x(t); Rx(t) – ненормированная АКФ случайного процесса x(t).
Кроме того, для оценки погрешности доступны и истинные значения требуемой АКФ в виде функции rt(t) от корреляционного сдвига t, на основании которой рассчитываются параметры формирователя F1 (рис. 1). Дискретные значения этой нормированной АКФ обозначим через вектор rt. В дальнейшем посредством r(t) будем обозначать нормированную АКФ, то есть rx(t) = Rx(t)/s2x и rx(0) = 1, где s2x – дисперсия случайного процесса x(t); Rx(t) – ненормированная АКФ случайного процесса x(t).
В качестве меры погрешности, как правило, используется некоторое расстояние между АКФ [6], например, для функций ra(t)и rb(t):
Dab = ||q(t)[ra(t) – rb(t)]||, (1)
где q(t) – некоторая весовая функция, учитывающая снижение значимости корреляции с увеличением корреляционного сдвига t. В частном случае для непрерывных АКФ выражение (1) можно записать как  или
или
 . (2)
. (2)
Здесь во втором выражении учтено свойство четности АКФ. Формальный сомножитель, стоящий перед интегралом, может быть исключен, так как оценка точности метода производится в относительном виде, поэтому в дальнейших вычислениях сомножитель не используется. Весовая функция q(t) не имеет существенного влияния при относительной оценке, поэтому в дальнейшем она будет опущена.
Приведенное выражение (2) соответствует непрерывному случаю. Переходя к требуемому дискретному случаю, перепишем его в виде  , где ra =[ra] и rb =[rb] – дискретное представление для функций ra(t) и rb(t); n – максимальный корреляционный сдвиг (размер векторов ra и rb). Дальнейшие преобразования приводят к стандартному виду среднеквадратичного отклонения. Действительно, исключив зависимость значения погрешности от величины корреляционного сдвига и приведя результат к размерности АКФ, получаем
, где ra =[ra] и rb =[rb] – дискретное представление для функций ra(t) и rb(t); n – максимальный корреляционный сдвиг (размер векторов ra и rb). Дальнейшие преобразования приводят к стандартному виду среднеквадратичного отклонения. Действительно, исключив зависимость значения погрешности от величины корреляционного сдвига и приведя результат к размерности АКФ, получаем
 . (3)
. (3)
На основе одной теоретической (rt) и двух эмпирических АКФ ( ,
,  m), применив выражение (3), можно построить три оценки погрешностей моделирования. Рассмотрим их поочередно.
m), применив выражение (3), можно построить три оценки погрешностей моделирования. Рассмотрим их поочередно.
Первая оценка погрешности будет определяться выражением вида
 . (4)
. (4)
Выражение (4) отображает погрешность моделирования АКФ ведущего процесса. В предлагаемом методе формирование заданной АКФ для ведущего процесса базируется на соотношении
 , (5)
, (5)
где h(t) – импульсная характеристика формирующего фильтра; Re(t), Rx(t) – АКФ сигнала на входе и выходе фильтра соответственно. Если входной сигнал e(t) – белый шум с интенсивностью Ф0, то есть Re(t) = 2pФ0d(t), где d(t) – дельта-функция, то  .
.
 Таким образом, АКФ стохастического процесса на выходе линейного фильтра полностью оп- ределяется импульсной характеристикой последнего, то есть применение выражения (5) для мо- делирования не порождает дополнительных погрешностей, за исключением обусловленных реализацией метода [7], которые в первом приближении будем считать незначимыми. На основании вышеизложенного можно предположить, что основной составляющей в оценке (4) будет погрешность, обусловленная вариативностью оценок АКФ, то есть она будет носить случайный характер. Значение этой погрешности сложным образом зависит от длины анализируемого вектора N, вида АКФ и значений ее параметров, корреляционного сдвига n, но в пределе при N ®¥ погрешность Dmt также будет стремиться к нулю (Dmt ® 0).
Таким образом, АКФ стохастического процесса на выходе линейного фильтра полностью оп- ределяется импульсной характеристикой последнего, то есть применение выражения (5) для мо- делирования не порождает дополнительных погрешностей, за исключением обусловленных реализацией метода [7], которые в первом приближении будем считать незначимыми. На основании вышеизложенного можно предположить, что основной составляющей в оценке (4) будет погрешность, обусловленная вариативностью оценок АКФ, то есть она будет носить случайный характер. Значение этой погрешности сложным образом зависит от длины анализируемого вектора N, вида АКФ и значений ее параметров, корреляционного сдвига n, но в пределе при N ®¥ погрешность Dmt также будет стремиться к нулю (Dmt ® 0).
Так, для гауссовского стационарного процесса x(t) с АКФ вида rx(t) = e–a|t| на интервале наблюдения T дисперсия оценок АКФ будет определяться выражением
 , (6)
, (6)
где 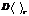 – дисперсия среднего на интервале T, T = N × Dt, Dt – шаг дискретизации по времени, в дальнейшем для простоты будем считать, что Dt = 1 (то есть T = N) [8]. Следует отметить, что (6) носит приблизительный характер [8] и верно только в случае выполнения неравенства
– дисперсия среднего на интервале T, T = N × Dt, Dt – шаг дискретизации по времени, в дальнейшем для простоты будем считать, что Dt = 1 (то есть T = N) [8]. Следует отметить, что (6) носит приблизительный характер [8] и верно только в случае выполнения неравенства
aT ³106. (7)
Таким образом, как видно из (6), изменение параметра АКФ приводит к изменению случайной составляющей погрешности моделирования, определяемой выражением (4).
Вторая оценка погрешности будет определяться выражением
 . (8)
. (8)
В данной оценке погрешности присутствуют две составляющие. Основная из них – методическая погрешность, имеющая систематический характер. Источником этой погрешности является невозможность точного сопоставления значений пар при ранжировании элементов векторов Pm и Ps² при различающихся законах распределения.
На рисунке 2 приведены примеры ранжированных векторов Pa и Pb, элементы которых распределены на совпадающих интервалах [0, 1]: в первом случае по разным законам распределения (рис. 2а), во втором случае законы распределения совпадают (рис. 2б).
Вполне очевидно, что и АКФ стохастического процесса, сформированного из вектора Pb путем перестановок, будет отличаться от АКФ вектора Pa. Во втором случае (рис. 2б) АКФ также будут отличаться, но значительно меньше, и самое главное, это отклонение будет иметь случайный, а не систематический характер, при N ®¥ отклонение будет стремиться к нулю. Именно эту погрешность авторы метода определили как основную и в работе [3] описали механизм ее возникновения.
Следует отметить одну особенность методической погрешности: она сложным образом зависит от распределений, параметров и вида АКФ. Кроме того, с изменением параметров АКФ будет изменяться и погрешность. Это связано с тем, что формирование ведущего процесса (вектор Pm) в предлагаемом варианте реализации производится на основе линейного динамического преобразования Pm¢. Такое преобразование изменяет любой закон распределения вероятностей, если он не является нормальным, происходит так называемая нормализация. Очевидно, чем больше инерционность формирователя АКФ (см. F1 на рис. 1), тем сильнее будет трансформирован закон распределения выходного процесса.
Ниже приведен пример для отвлеченного случайного процесса e(t), имеющего распределение арксинуса (закон распределения выбран из соображений наглядности). Для формирования случайного процесса x(t) с АКФ вида
rx(t) = e–a|t|, (9)
где a – параметр АКФ, определяющий скорость ее убывания, использован фильтр вида xi = aei + bxi–1, где a и b – параметры фильтра, определяемые на основе заданного параметра a [7]. Результаты численного эксперимента показаны на рисунке 3.
Результаты проведенного эксперимента показывают, что уменьшение параметра a при формировании АКФ вида (9) приводит к изменению закона распределения выходного процесса, а следовательно, и к росту систематической погрешности. Можно с большой уверенностью предположить, что данное утверждение является верным для всех законов распределения, за исключением нормального закона, который инвариантен относительно линейного динамического преобразования.
Третья возможная оценка погрешности формирования АКФ будет определяться выражением
 , (10)
, (10)
 которое определяет «расстояние» между теоре- тически заданной АКФ и результатом моделирования. Именно эта погрешность и представляет наибольший интерес, поскольку характеризует точность конечного результата метода моделирования. Правомерно предположить, что в данной погрешности будут составляющие, имеющие систематический характер (методическая погрешность), и случайная составляющая (вариации оценок АКФ). В силу того, что составляющие погрешности (10) зависят от параметров АКФ, в частности от параметра a для АКФ вида (9), и сама погрешность будет зависеть от тех же параметров.
которое определяет «расстояние» между теоре- тически заданной АКФ и результатом моделирования. Именно эта погрешность и представляет наибольший интерес, поскольку характеризует точность конечного результата метода моделирования. Правомерно предположить, что в данной погрешности будут составляющие, имеющие систематический характер (методическая погрешность), и случайная составляющая (вариации оценок АКФ). В силу того, что составляющие погрешности (10) зависят от параметров АКФ, в частности от параметра a для АКФ вида (9), и сама погрешность будет зависеть от тех же параметров.
Для анализа методической погрешности и ее зависимости от параметров АКФ необходимо уменьшить влияние случайной составляющей, что можно сделать двумя способами. Первый способ связан с увеличением интервала наблюдения (длины векторов) и количества параллельных экспериментов с последующим усреднением.
Второй способ заключается в фиксировании дисперсии оценки АКФ в соответствии с выражением (6), для этого необходимо, чтобы aT = const. В таком случае при изменении параметра a будет изменяться только значение методической погрешности, значение случайной погрешности должно оставаться на одном уровне. Опишем алгоритм, реализующий предлагаемый метод.
1. Задаем [amin, amax] – интервал изменения параметра АКФ и Da – шаг изменения, предполагая, что АКФ имеет только один параметр, например случай (9). Определяем, до какого значения АКФ rE проводится анализ погрешности. Задаем коэффициент кратности K, определяющий, во сколько раз длина вектора N будет превышать длину корреляционного сдвига.
2. Определяем очередное значение ai = amin + + i × Da. Для этого вычислим корреляционный сдвиг tE исходя из заданного значения АКФ rE, решив уравнение r(t) – rE = 0.
3. Округляем полученное значение tE до ближайшего целого n, поскольку корреляционный сдвиг для стохастических процессов, представленных векторами, есть целая величина. Далее пересчитываем значение ai с учетом округления. Рассчитываем общую длину вектора N = nK.
4. Проводим цикл моделирования и вычисляем оценки погрешности по (4), (8) и (10).
5. Если ai < amax, переходим на шаг 2, иначе завершаем расчет.
Для проверки приведенных предположений были выполнены численные эксперименты. В частности, рассмотрены три характерных случая параметров моделирования, результаты которых приведены ниже. Во всех трех случаях моделировались случайные процессы, с АКФ вида (9) коэффициент кратности K выбирался исходя из условия (7), диапазон изменения параметра a от 0,1 до 2,0, всего 10 точек.
Случай 1. Законы распределения векторов Pm, Pm¢ и Ps² совпадают. Такое возможно только при условии, что все три вектора будут иметь нормальное распределение. Заметим, что данное сочетание законов распределений не имеет практической значимости, поскольку результат моделирования, вектор Ps, будет иметь нормальное распределение, а, как уже указывалось ранее, такую задачу можно решить и без привлечения алгоритмов перестановок.
Подобное сочетание законов распределения позволяет изменять параметры формирующего фильтра F1 без изменения закона распределения элементов вектора Pm. В силу того, что у ведущего и ведомого процессов законы распределения совпадают, в результатах моделирования будет отсутствовать методическая погрешность, а применение алгоритма масштабирования длины вектора в зависимости от значения параметра a позволит сохранить дисперсию случайной погрешности на одном уровне.
 Таким образом, можно предположить, что Dst = const, Dms = const и Dmt = const во всем диапазоне значений параметра a. В качестве критериев оценки верности выдвинутого предположения воспользуемся критерием значимости регрессии и критерием Аббе–Линника. В первом случае, исходя из предположения, что погрешность есть функция параметра a, представим ее в виде линейной модели D(a) = b0+ b1a + h с коэффициентами регрессии b0, b1 и случайной составляющей h. После оценки коэффициентов b0, b1 проводилась проверка значимости линейной регрессии на основе критерия Фишера:
Таким образом, можно предположить, что Dst = const, Dms = const и Dmt = const во всем диапазоне значений параметра a. В качестве критериев оценки верности выдвинутого предположения воспользуемся критерием значимости регрессии и критерием Аббе–Линника. В первом случае, исходя из предположения, что погрешность есть функция параметра a, представим ее в виде линейной модели D(a) = b0+ b1a + h с коэффициентами регрессии b0, b1 и случайной составляющей h. После оценки коэффициентов b0, b1 проводилась проверка значимости линейной регрессии на основе критерия Фишера:  , где R2 – коэффициент детерминации; f1 – количество объясняющих переменных, в данном случае f1 = 1, f2 = m – f1 – 1 – число степеней свободы необъясненной дисперсии, m – количество экспериментальных точек, f2 = 8. Критическое значение статистики Фишера при указанных параметрах и при уровне значимости p = 0,05 составляет Fcr = 5,32. Регрессия признается значимой при выполнении условия F > Fcr.
, где R2 – коэффициент детерминации; f1 – количество объясняющих переменных, в данном случае f1 = 1, f2 = m – f1 – 1 – число степеней свободы необъясненной дисперсии, m – количество экспериментальных точек, f2 = 8. Критическое значение статистики Фишера при указанных параметрах и при уровне значимости p = 0,05 составляет Fcr = 5,32. Регрессия признается значимой при выполнении условия F > Fcr.
Критерий Аббе–Линника позволяет проверить гипотезу об отсутствии тренда в погрешностях на основе следующей статистики [9]:
 .
.
Если q ³ qcr, то нет оснований отвергнуть гипотезу, что наблюдаемые значения не содержат тренда, в противном случае считаем, что тренд есть. Для рассматриваемых условий проведения численного эксперимента qcr = 0,531 при уровне значимости p = 0,05 [10].
Численные значения полученных статистик приведены в таблице, в графическом виде результаты представлены на рисунке 4а.
Как видно из приведенных графиков, оценки погрешности Dst и Dmt совпали и, как следствие, совпали линии регрессии. Это означает, что ведомый процесс практически точно воспроизвел ведущий процесс. Наблюдаемый на графиках наклон линии регрессии, очевидно, следует отнести к некомпенсированному увеличению вариативности оценки АКФ с уменьшением параметра a. Но использованные статистические критерии значимость наклона не подтверждают (см. табл.), так что можно считать, что разработанный алгоритм масштабирования с поставленной задачей справился.
 Наклон линии регрессии погрешности Dms имеет подтверждение значимости по обоим критериям. Механизм увеличения «расстояния» между ведущим и ведомым процессами заключается в уменьшении количества вариантов при сглаживании ведущего процесса (при уменьшении a). Однако значимого влияния на результат моделирования эта погрешность не имеет, так как на два порядка меньше, чем погрешность Dst.
Наклон линии регрессии погрешности Dms имеет подтверждение значимости по обоим критериям. Механизм увеличения «расстояния» между ведущим и ведомым процессами заключается в уменьшении количества вариантов при сглаживании ведущего процесса (при уменьшении a). Однако значимого влияния на результат моделирования эта погрешность не имеет, так как на два порядка меньше, чем погрешность Dst.
Случай 2. Рассмотрим случай, когда вектор Pm имеет нормальный закон распределения, а элементы вектора Ps² распределены по закону арксинуса. Эксперимент проведен по аналогии с предыдущим случаем, а результаты расчета статистик представлены в таблице, в графическом виде результаты отображены на рисунке 4б.
Как видно из результатов эксперимента, однозначно говорить о наличии зависимости погрешности моделирования от параметра a нельзя. Действительно, принципиально «расстояние» между векторами остается неизменным, как и в предыдущем эксперименте, так как законы распреде- ления ведущего и ведомого векторов остаются неизменными. Наблюдаемый наклон линии регрессии, очевидно, имеет ту же природу, что и в предыдущем случае.
Случай 3. Особый интерес представляет третий случай, когда элементы вектора Pm¢ распределены по закону арксинуса, а элементы вектора Ps² – по нормальному закону. Очевидно, что распределение элементов вектора Pm будет изменяться с изменением параметра a (параметров фильтра F1 на рис. 1). При этом уменьшение параметра a (увеличение постоянной времени фильтра F1 на рисунке 1) будет нормализовать закон распределения Pm (см. рис. 3). Таким образом, «расстояние» между векторами Ps² и Pm будет уменьшаться. Если выдвинутое предположение верно, то на графиках зависимости погрешностей от параметра a будет наблюдаться положительный наклон линий регрессии. Графики на рисунке 4в подтверждают выдвинутое предположение визуально, а расчет статистик Аббе–Линника и Фишера, приведенный в таблице, подтверждает статистическую значимость наклона линии регрессии.
Результаты рассмотренного случая моделирования позволяют говорить о том, что подтверждается модель возникновения погрешности моде- лирования случайных процессов анализируемым методом перестановок. Для убедительности рассмотрим еще один случай.
Случай 4. Рассмотрим случай, когда элементы вектора Ps² и вектора Pm¢ распределены по закону арксинуса. Очевидно, что, как и в предыдущем случае, распределение элементов вектора Pm будет изменяться в зависимости от параметра a.
Численные значения полученных статистик приведены в таблице, в графическом виде результаты представлены на рисунке 4г.
Как и в предыдущем случае, результирующая погрешность Dst имеет статистически значимый наклон линии регрессии, но этот наклон уже имеет отрицательный знак.
На основании результатов, полученных в данной работе, можно сделать следующие выводы.
Данный метод расчета параметров проведения эксперимента по анализу погрешности моделирования позволяет значительно снизить влияние вариационной составляющей погрешности оценки АКФ, в результате чего появляется возможность выделить методическую составляющую и оценить ее реальный вклад в суммарную погрешность.
Проведенные численные эксперименты показывают, что сделанное предположение о механизме возникновения методической погрешности можно считать верным. Действительно, в первых двух случаях, когда «расстояние» между ведущим и ведомым векторами не зависит от параметра АКФ, наклон линии регрессии результирующей погрешности Dst статистически незначим. Иными словами, погрешность моделирования не зависит от параметра АКФ. В двух последних случаях «расстояние» зависит от параметра АКФ и, как следствие, наклон линии регрессии погрешности Dst становится статистически значимым.
Несмотря на наличие методической погрешности, метод имеет очень значимое преимущество, о котором говорилось в начале статьи, – отсутствие ограничений на вероятностную и спектральную меру моделируемого случайного процесса. Очевидно, что можно найти модификации данного метода, позволяющие снизить выявленную методическую погрешность, но это будет задачей дальнейших исследований.
Литература
1. L’Ecuyer P. Non-uniform Random Variate Generations. Intern. Encyclopedia of Statistical Science, Springer-Verlagpp, 2011, Part 14, pp. 991–995.
2. Gregory K. Miller Probability: Modeling and Applications to Random Processes. Wiley-Interscience, 2006, 488 p.
3. Polge R.J., Holliday E.M., Bhagawan B.K. Generation of a pseudo-random set with desired correlation and probability distribution, Simulation, May 1973, pp. 153–158.
4. Лебедев А.Н. [и др.]. Вероятностные методы в инженерных задачах: справочник. СПб: Энергоатомиздат, 2000. 329 с.
5. Вадзинский Р.Н. Справочник по вероятностным распределениям. М.: Наука, 2001. 149 с.
6. Пригарин С.М. Методы численного моделирования случайных процессов и полей. Н.: Изд-во ИВМиМГ СО РАН, 2005. 259 с.
7. Прохоров С.А. Математическое описание и моделирование случайных процессов. Самара: Изд-во Самарского гос. аэрокосм. ун-та, 2001. 209 с.
8. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 2003. 832 с.
9. Линник Ю.В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. М.: Физматлит, 1958. 336 с.
10. Rajagopalan V. Selected Statistical Tests. ND, India, New Age Intern., 2006, 260 р.
References
1. L’Ecuyer P. Non-uniform Random Variate Generations. International Encyclopedia of Statistical Science. Springer-Verlag Publ.,
2011, part 14, pp. 991–995.
2. Gregory K. Miller Probability: Modeling and Applications to Random Processes. Wiley-Interscience Publ., 2006, 488 p.
3. Polge R.J., Holliday E.M., Bhagawan B.K. Generation of a pseudo-random set with desired correlation and probability distribution.
Simulation. May 1973, pp. 153–158.
4. Lebedev A.N. Veroyatnostnye metody v inzhenernykh zadachakh [Probability Methods in Engineering Challenges]. St. Peterburg,
Energoatomizdat Publ., 2000, 329 p.
5. Vadzinsky R.N. Spravochnik po veroyatnostnym raspredeleniyam [Reference Book]. St. Peterburg, Nauka Publ., 2001, 149 p.
6. Prigarin S.M. Metody chislennogo modelirovaniya sluchaynykh protsessov i poley [The Methods of Numerical Simulation of Sto-chastic Processes and Fields]. Novosibirsk, IVMiMG SO RAN Publ., 2005, 259 p.
7. Prokhorov S.A. Matematicheskoe opisanie i modelirovanie sluchaynykh protsessov [Mathematical Formulation and Simulation of
Stochastic Processes]. Samara, Samar. St. Aerokosm. Univ. Publ., 2001, 209 p.
8. Korn G., Korn T. Spravochnik po matematike dlya nauchnykh rabotnikov i inzhenerov [Matematics Guide for Scientists and Engi-neers]. Moscow, Nauka Publ., 2003, 832 р.
9. Linnik Yu.V. Metod naimenshikh kvadratov i osnovy matematiko-statisticheskoy teorii obrabotki nablyudeny [A Least-Squares
Method and Basics of Mathematics and Statistics Theory of Observations Processing]. Moscow, Fizmatlit Publ., 1958, 336 р.
10. Rajagopalan V. Selected Statistical Tests. ND, India, New Age Intern. Publ., 2006, 260 р.

 .
. и
и  Кроме того, для оценки погрешности доступны и истинные значения требуемой АКФ в виде функции rt(t) от корреляционного сдвига t, на основании которой рассчитываются параметры формирователя F1 (рис. 1). Дискретные значения этой нормированной АКФ обозначим через вектор rt. В дальнейшем посредством r(t) будем обозначать нормированную АКФ, то есть rx(t) = Rx(t)/s2x и rx(0) = 1, где s2x – дисперсия случайного процесса x(t); Rx(t) – ненормированная АКФ случайного процесса x(t).
Кроме того, для оценки погрешности доступны и истинные значения требуемой АКФ в виде функции rt(t) от корреляционного сдвига t, на основании которой рассчитываются параметры формирователя F1 (рис. 1). Дискретные значения этой нормированной АКФ обозначим через вектор rt. В дальнейшем посредством r(t) будем обозначать нормированную АКФ, то есть rx(t) = Rx(t)/s2x и rx(0) = 1, где s2x – дисперсия случайного процесса x(t); Rx(t) – ненормированная АКФ случайного процесса x(t). или
или . (2)
. (2) , где ra =[ra] и rb =[rb] – дискретное представление для функций ra(t) и rb(t); n – максимальный корреляционный сдвиг (размер векторов ra и rb). Дальнейшие преобразования приводят к стандартному виду среднеквадратичного отклонения. Действительно, исключив зависимость значения погрешности от величины корреляционного сдвига и приведя результат к размерности АКФ, получаем
, где ra =[ra] и rb =[rb] – дискретное представление для функций ra(t) и rb(t); n – максимальный корреляционный сдвиг (размер векторов ra и rb). Дальнейшие преобразования приводят к стандартному виду среднеквадратичного отклонения. Действительно, исключив зависимость значения погрешности от величины корреляционного сдвига и приведя результат к размерности АКФ, получаем . (3)
. (3) ,
,  m), применив выражение (3), можно построить три оценки погрешностей моделирования. Рассмотрим их поочередно.
m), применив выражение (3), можно построить три оценки погрешностей моделирования. Рассмотрим их поочередно. . (4)
. (4) , (5)
, (5) .
.
 , (6)
, (6)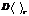 – дисперсия среднего на интервале T, T = N × Dt, Dt – шаг дискретизации по времени, в дальнейшем для простоты будем считать, что Dt = 1 (то есть T = N) [8]. Следует отметить, что (6) носит приблизительный характер [8] и верно только в случае выполнения неравенства
– дисперсия среднего на интервале T, T = N × Dt, Dt – шаг дискретизации по времени, в дальнейшем для простоты будем считать, что Dt = 1 (то есть T = N) [8]. Следует отметить, что (6) носит приблизительный характер [8] и верно только в случае выполнения неравенства . (8)
. (8) , (10)
, (10)

 , где R2 – коэффициент детерминации; f1 – количество объясняющих переменных, в данном случае f1 = 1, f2 = m – f1 – 1 – число степеней свободы необъясненной дисперсии, m – количество экспериментальных точек, f2 = 8. Критическое значение статистики Фишера при указанных параметрах и при уровне значимости p = 0,05 составляет Fcr = 5,32. Регрессия признается значимой при выполнении условия F > Fcr.
, где R2 – коэффициент детерминации; f1 – количество объясняющих переменных, в данном случае f1 = 1, f2 = m – f1 – 1 – число степеней свободы необъясненной дисперсии, m – количество экспериментальных точек, f2 = 8. Критическое значение статистики Фишера при указанных параметрах и при уровне значимости p = 0,05 составляет Fcr = 5,32. Регрессия признается значимой при выполнении условия F > Fcr. .
.
