Расчет биотехнологических процессов требует, как правило, разработки алгоритмического и программного обеспечения в силу использования нелинейных кинетических соотношений.
Результатами расчетов являются значения таких выходных показателей, как концентрация субстрата, концентрация биомассы и продукта, по которым вычисляется продуктивность по целевому компоненту. Исходной информацией для расчета, кроме кинетических параметров, являются концентрации субстрата в поступающем потоке Sf, г/л, величина протока D(D = Q/V), где Q – объемная скорость поступающего потока, м3/ч, V – объем заполнения ферментера, м3, и для системы с рециркуляцией – величина протока рециркуляции DR (DR=QR/V), где QR – величина потока рециркуляции, м3/ч.
Разработка алгоритмического и программного обеспечения базируется на использовании математических моделей, основными требованиями к которым является наличие надежных (адекватных) кинетических соотношений. Для разных процессов виды кинетических соотношений могут быть различными с учетом тех или иных особенностей процессов [1–3], отметим лишь, что большинство из них являются нелинейными относительно концентраций действующих компонентов. Анализ кинетических соотношений и их использование при моделировании процессов позволяют выявить особенности последних, которые иногда невозможно прогнозировать экспериментально. Так, в работе [3] показаны возможности оценки предельного значения величины протока D, при котором субстрат полностью вымывается из ферментера, не вступив в процесс синтеза; существования множественности стационарных состояний, обеспечивающих одинаковое значение продуктивности; оценки входных технологических показателей, обеспечивающих максимальную продуктивность.
В настоящей статье описывается разработка алгоритмического и программного обеспечения более сложного по сравнению с [3] процесса в связи с использованием рециркуляции субстрата и биомассы с полным выделением продукта из потока циркуляции. Рециркуляция дает возможность увеличить величину протока и продуктивность процесса по целевому компоненту, как это было показано в [4]. Во многих исследованиях влияние рециркуляции на процессы микробиологического синтеза отмечается как возможное существенное улучшение показателей [5, 6].
Однако в таких микробиологических направлениях, как производство спирта, рециркуляция успешно используется даже на производстве [7, 8]. Наиболее существенно она может влиять на условия устойчивости функционирования биореакторов, особенно когда в контур рециркуляции включен мембранный модуль [9]. В то же время в информационном портале по подбору оборудования “Pharm System” вопросы учета рециркуляции не получили освещения [10], что, естественно, может отразиться на результатах подбора.
Наличие рецикла, с одной стороны, расширяет технологические возможности в части повышения продуктивности, с другой – требует более четкого обоснования ограничений, невыполнение которых может привести к неосуществимости практической реализации процесса [4].
Алгоритмическое и программное обеспечение разработано для процесса с непрерывным функционированием и непрерывным отводом продукта из потока после ферментера.
Расчетные соотношения
Кинетические соотношения [1, 2, 4]:
 (1)
(1)
 . (2)
. (2)
Уравнения математической модели (материальный баланс) [6]:
–D×X + µ×X = 0, (3)
 , (4)
, (4)
–(D + DR) × P + (a × µ + b) × X = 0. (5)
Продуктивность по целевому компоненту:
QP = (D + DR) P. (6)
Решим систему (3)–(5) с учетом (1), (2) и условия
Sf > S > 0, (7)
получаем:  (8)
(8)
 . (9)
. (9)
Решение не существует или неприемлемо при
A < 0, B >0, (10)
где A = a1 – (D + DR) D × a2, (11)
B = a1 × Sf – (D + DR) a2 × a3, (12)
C = (D + DR) D × a2 × Km × Ki, (13)
a1 = a × D + b, (14)
 , (15)
, (15)
a3 = Ki (µmax – D), (16)
m = Ki × YX/S × µmax. (17)
Последнее означает, что ни при каких значениях D, DR и Sf, обеспечивающих выполнение условия, технологический процесс нереализуем.
Существование решения (8) и (9) при A < 0 определяется условием неотрицательности дискриминанта:
B2 + 4 A × C ³ 0 (при A < 0) . (18)
Выражение для дискриминанта:
 (19)
(19)
где g = (D + DR).
Из равенства дискриминанта нулю получаем оценку для DR=DRd:
 , (20)
, (20)
где 
 (21)
(21)
Таким образом, реальное осуществление процесса с рециркуляцией обеспечивается неотрицательностью соотношения (21), откуда получаем ограничение по D:
 . (22)
. (22)
Решение (22):
 . (23)
. (23)
Нетрудно видеть, что, если A < 0 и D = µmax, то B > 0, то есть решение неприемлемо. Отсюда следует, что D всегда должно быть меньше µmax.
Таким образом, в знаменателе выражения (23) следует принять знак «+», то есть
 . (24)
. (24)
 Отсюда имеем условие:
Отсюда имеем условие:
 . (25)
. (25)
При выражении 
получаем  . (26)
. (26)
Численный анализ показал, что, хотя условие (26) дает неотрицательность F, получаемое значение DRd может привести к отрицательному значению дискриминанта (18). Отрицательное значение в (18) получается и при условии равенства в (25). Вычислим Sf по условию равенства в (25), обозначив SfC. Значение Sf вычисляется по уравнению
 . (27)
. (27)
Получаем 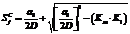 (28)
(28)
и при D по формуле (24)
 . (29)
. (29)
Значение DR вычисляется по условию
 .(30)
.(30)
Как отмечалось ранее, расчетные соотношения определяются знаком величин A и B. Если значение D дает отрицательный знак A, этот знак сохраняется при любом DR. Вычислим D, при котором A = 0 (для DR = 0), обозначив DA:
 . (31)
. (31)
Область задания D делится на две подобласти:
D > DA, A < 0, (32)
D < DA, A > 0. (33)
Однако последнее неравенство может быть изменено за счет значения DR. Значение DR = DRA, при котором A = 0 в условиях D < DA:
 . (34)
. (34)
Отсюда следует:
если DR > DRA при D < DA, A < 0, (35)
если DR < DRA при D < DA, A > 0. (36)
Значение Sf = Sf B, определяющее знак B при DR = 0 и любом значении D:
 . (37)
. (37)
При этом,
если Sf > Sf B, B > 0, (38)
если Sf < Sf B, B < 0. (39)
Первое неравенство может быть изменено в зависимости от значения DRB, при котором B = 0:
 . (40)
. (40)
Таким образом, при Sf < SfB имеем условие
DRB < 0. (41)
Если DR < DRB, то B > 0; (42)
если DR > DRB, то B < 0. (43)
 В результате получены расчетные соотношения, позволяющие формировать алгоритм расчета (см. табл. 1).
В результате получены расчетные соотношения, позволяющие формировать алгоритм расчета (см. табл. 1).
Блок-схема алгоритма вычисления показателей процесса
 Для задания исходных данных необходимо предварительно сделать вычисления, результаты которых обеспечивают условия реального осуществления процесса.
Для задания исходных данных необходимо предварительно сделать вычисления, результаты которых обеспечивают условия реального осуществления процесса.
Вычислить минимальное значение Sf по формуле (29).
Исходное значение для расчета Sf должно быть принято по условию Sf > minSf.
Вычислить максимальное значение D по формуле (24).
Исходное значение D должно быть принято по условию 0 < D < maxD.
Вычислить значение DA, определяющее знак A при DR = 0, по формуле (31).
Вычислить m по формуле (17).
Поскольку величина протока рециркуляции определяется в процессе реализации алгоритма по значению продуктивности, в исходные данные для расчета, кроме кинетических констант, значений Sf и D, вводятся точность поиска величины продуктивности ε и фактор шага поиска величины протока рециркуляции h. Шаг поиска вычисляется по соотношению H=h·D.
Величина ε ограничена значением 1,0, то есть ε < 1,0.
Алгоритм включает два направления расчета, определяемые исходным значением D: для D > DA (D < Dmax) и для D < DA (D > 0).
Исходные данные для расчета одни и те же для обеих ветвей алгоритма.
Расчетные соотношения, включенные в блок-схему алгоритма, следующие: µmaxч-1 = 0,48, Pm г/л = 50, Km г/л = 1,2, Ki г/л = 22, YX/S = 0,4, α г/л= 2,2, β ч–1 = 0,2.
 Блок-схема алгоритма расчета показана на рисунке 1.
Блок-схема алгоритма расчета показана на рисунке 1.
Реализация алгоритма была выполнена в качестве компьютерной программы для ОС Windows (XP, Vista, 7, 8.x) в среде разработки Visual Studio 2010 на языке программирования C++ и скомпилирована в исполнимый файл на стандартном носителе.
Внешне программа состоит из двух компонентов. Окно программы (рис. 2) визуально разбито на три части. Ввод данных осуществляется в полях «Кинетические параметры» и «Технологические параметры», после нажатия кнопки «Вычислить» происходят вычисления и вывод информации в полях области «Результат». При нажатии на кнопку «Справка» отобразятся справка по параметрам программы и краткое руководство по работе с ней.
Особенность программы заключается в том, что пользователь должен задать фактор шага поиска величины протока циркуляции h и точность поиска величины продуктивности ε. Указанные величины h и ε задаются по усмотрению пользователя. Рекомендуемые значения: h=0,5; ε=0,02 (то есть 2 %).
В результате работы программы получаем значения концентраций компонентов на выходе из ферментера соответственно S, г/л; X, г/л; P, г/л, и количество отводимого продукта QP, г·л-1ч-1.
Некоторые численные результаты по данным расчетов параметров процесса [5] приведены в таблице 2.
В заключение отметим, что разработанные алгоритм и программа расчета показателей биотехнологического процесса для кинетических соотношений, используемых при получении различных продуктов микробиологического синтеза в широкой области исходных данных для процесса ферментации, имеют свои особенности. В зависимости от численных значений констант практическая реализация процесса синтеза должна учитывать ряд ограничений, накладываемых на входные показатели процесса Sf, D и DR, что невозможно оценить экспериментально. Так, по блок-схеме алгоритма возможность практической реализации процесса синтеза содержит 21 вариант. Разработанный общий подход к обеспечению расчетов микробиологического синтеза в процессе с циркуляцией предполагает возможность использования в качестве целевого продукта биомассы, учет возможности неполного отделения продукта (например, при мембранном разделении), оценку эффективности использования субстрата. Во всех численных примерах расчета показано, что введение циркуляции обеспечивает повышение продуктивности по целевому продукту.
Литература
1. Henson M.A., Seborg D.E. Nonlinear control strategies for continuous fermenters. Chemical Engineering Science, 1992, vol. 47, no. 4, pp. 821–835.
2. Agrawal P., Koshy G., Ramseier M. An algorithm for operating a fed-batch fermentor at optimum specific growth rate. Biotechnology and bioengineering, 1989, vol. 33, no. 1, pp. 115–125.
3. Гордеева Ю.Л., Щербинин М.Ю., Гордеев Л.С., Комиссаров Ю.А. Стационарные состояния биотехнологических процессов с нелинейной кинетикой роста микроорганизмов. Множественность при заданной величине концентрации субстрата в поступающем потоке // Вестник Астраханского государственного технического университета. Сер.: Управление, вычислительная техника и информатика. 2013. № 1.
4. Гордеева Ю.Л., Глебов М.Б., Гордеев Л.С. Оптимизация процесса микробиологического синтеза с нелинейной кинетикой роста микроорганизмов и рециркуляцией субстрата и биомассы // Теоретические основы химической технологии. 2013. Т. 47. № 5. C. 594–596.
5. Меньшутина Н.В., Гусева Е.В., Нижегородова Т.А., Будран Ж. Механические воздействия на микроорганизмы при культивировании // Биотехнология. 2007. № 5. С. 78–85.
6. Меньшутина Н.В., Гусева Е.В., Нижегородова Т.А., Будран Ж., Горгиен Ж.Л., Гедон Э., Делоне С. Математическое моделирование производства L-глутаминовой кислоты // Изв. вузов. Химия и химическая технология. 2007. Т. 50. С. 93–98.
7. Yarovenko V.L. Theory and practice of continuous cultivation of microorganisms in industrial alcoholic processes. Advances in Biochemical Engineering, Springer Berlin Heidelberg, 1978, vol. 9, pp. 1–30.
8. Warren R.K., Macdonald D.G., Hill G.A. The design and costing of a continuous ethanol process using wheat and cell recycle fermentation. Bioresource technology, 1994, vol. 47, no. 2, pp. 121–129.
9. Меньшутина Н.В., Тарутина Н.В., Софиев А.Э. Анализ устойчивости функционирования мембранных биореакторов // ТОХТ. 2008. № 3. С. 251–256.
10. Меньшутина Н.В., Топтунов В.Н., Батин С.Э., Гусе- ва Е.В. Информационный портал для подбора оборудования “Pharm System” // Программные продукты и системы. 2009. № 1 (85). С. 68–69.
References
1. Henson M.A., Seborg D.E. Nonlinear control strategies for continuous fermenters. Chemical Engineering Science.
1992, vol. 47, no. 4, pp. 821–835.
2. Agrawal P., Koshy G., Ramseier M. An algorithm for operating a fed-batch fermentor at optimum specific growth
rate. Biotechnology and Bioengineering. 1989, vol. 33, no. 1, pp. 115–125.
3. Gordeeva Yu.L., Shcherbinin M.Yu., Gordeev L.S., Komissarov Yu.A. Stationary states of biotechnological process-es with nonlinear kinetics of growth of microorganisms. Plurality at the given value of substrate concentration in the inco m-ing flow. Vestnik Astrakhanskogo gos. tekhnicheskogo univ. Seriya: Upravlenie, vychislitelnaya tekhnika i informatika
[Bulletin of Astrakhan State Technical University. Series: Management, Computer Science and Informatics]. 2013, no. 1,
pp. 21–28 (in Russ.).
4. Gordeeva Yu.L., Glebov M.B., Gordeev L.S. Optimization of Microbiological Synthesis with Nonlinear Kinetics of
Microorganism Growth and Recycling of Substrate and Biomass. Teoreticheskie osnovy khimicheskoi tekhnologii [Theoreti-cal Foundations of Chemical Engineering]. 2013, vol. 47, no. 5, pp. 612–614.
5. Menshutina N.V., Guseva E.V., Nizhegorodova T.A., Budran Zh. Mechanical influence on microorganisms in cult i-vation. Biotekhnologiya [Biotechnology]. 2007, no. 5, pp. 78–85 (in Russ.).
6. Menshutina N.V., Guseva E.V., Nizhegorodova T.A., Budran Zh., Gorgien Zh.L., Gedon E., Delone S. Mathematical
modeling of L-glutamine acid production. Izvestiya vysshykh uchebnykh zavedeny. Khimiya i khimicheskaya tekhnologiya
[News of Universities. Chemistry and Chemical Technology Research-Engineering Journ.]. 2007, vol. 50, pp. 93–98 (in
Russ.).
7. Yarovenko V.L. Theory and practice of continuous cultivation of microorganisms in industrial alcoholic processes.
Advances in Biochemical Engineering. Springer Berlin Heidelberg Publ., 1978, vol. 9, pp. 1–30.
8. Warren R.K., Macdonald D.G., Hill G.A. The design and costing of a continuous ethanol process using wheat and
cell recycle fermentation. Bioresource Technology. 1994, vol. 47, no. 2, pp. 121–129.
9. Menshutina N.V., Tarutina N.V., Sofiev A.E. Analysis of the Performance Stability of Membrane Bioreactors.
Teoreticheskie osnovy khimicheskoy tekhnologii [Theoretical Foundations of Chemical Engineering]. 2008, vol. 42, no. 3,
pp. 251–256.
10. Menshutina N.V., Toptunov V.N., Batin S.E., Guseva E.V. “Pharm System” data portal for equipment selection.
Programmnye produkty i sistemy [Software & Systems]. 2009, no. 1 (85), pp. 68–69 (in Russ.).
 (1)
(1) . (2)
. (2) , (4)
, (4) (8)
(8) . (9)
. (9) , (15)
, (15) (19)
(19) , (20)
, (20)
 (21)
(21) . (22)
. (22) . (23)
. (23) . (24)
. (24)
 . (25)
. (25)
 . (26)
. (26) . (27)
. (27)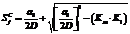 (28)
(28) . (29)
. (29) .(30)
.(30) . (31)
. (31) . (34)
. (34) . (37)
. (37) . (40)
. (40)


