В настоящее время в научных исследованиях и образовании, в производственной и других сферах деятельности человека определяющее значение имеют информационно-вычислительные системы. Развитие информатики и применение программных продуктов в научных исследованиях ставят вопрос о пересмотре основных концепций представления научных знаний и выдвигают на первый план задачу структурирования этих знаний [1]. Электронные образовательные ресурсы на основе современной компьютерной трехмерной симуляции физических процессов и явлений реализуются в форме мультимедийных учебно-научных лабораторий, или виртуальных тренажеров. Новизна технологии виртуальных тренажеров аргументируется использованием современных средств компьютерного моделирования и активным внедрением информационных технологий в сферу образования как нового трансдисциплинарного направления [2]. Именно с этой точки зрения внедрение информационных технологий способствует оптимальному решению вышеназванных задач и устранению ряда недостатков традиционного способа обучения. Эти вопросы во всей полноте можно решать с помощью мультимедийных учебно-научных лабораторий [3, 4].
Мультимедийная учебно-научная лаборатория, как правило, сочетает в себе имитационную динамическую модель оборудования и программную оболочку с методическим сопровождением лабораторной работы [5]. Программные средства – это математически обоснованная виртуальная модель, включающая систему графической визуализации, звуковое сопровождение и текстовую инфор- мацию [6]. Ввод и вывод информации осуществляются согласно разработанному алгоритму – программному коду виртуальной модели. Современные виртуальные тренажеры выполняются в трехмерной графике с максимальной имитацией материалов и освещения, что существенно повышает качество работы. Главной задачей здесь является приближение модели к реальному объекту за счет соблюдения правильных пропорций, размеров, цветовых решений и освещения [7, 8].
Моделирование является быстро развивающейся областью науки и техники. В технологии строительных композиционных материалов наряду с субстанционным (изготовление физического образца материала) и структурно-имитационным (имитация взаимодействия структурных элементов системы) моделированием широко применяется функциональное моделирование, результатом которого является получение некой математической функции, описывающей поведение объекта исследования, абстрагируясь от внутренней структуры вещественного субстрата. Функциональная модель работает по принципу «черного ящика», при этом известны параметры входа – переменные или постоянные факторы, а также параметры выхода – критерий эффективности, отклик и т.д. [9, 10].
Построение функциональных моделей экспериментальных зависимостей свойств бетона от его состава включает следующие этапы:
– уточнение оптимизируемых параметров (прочности бетона, удобоукладываемости бетонной смеси и др.) в зависимости от конкретной задачи;
– выбор факторов, определяющих изменчивость оптимизируемых параметров;
– определение основного исходного состава бетонной смеси;
– выбор интервалов варьирования факторов;
– выбор плана и условий проведения эксперимента;
– обработка результатов эксперимента с построением математических моделей зависимостей свойств бетонной смеси и бетона от выбранных факторов.
В данном исследовании выбран трехфакторный план эксперимента B-D13, который позволяет получать нелинейные квадратичные модели и обладает хорошими статистическими характеристиками. Основная цель разработки программно-алгоритмического средства обработки данных трехфакторного планированного эксперимента – изготовление программного продукта, позволяющего моментально рассчитать план и обработать выходные данные эксперимента. Разработка программы осуществлялась в среде визуального объектно-ориентированного программирования Microsoft Visual Basic. В качестве физического объекта исследования выбран мелкозернистый бетон, наполненный тонкомолотым известняком. Применялись сырьевые материалы: песок природный (мелкий, средний и повышенной крупности), портландцемент ЦЕМ I 42,5 Н (RЦ28=53,9 МПа), молотый известняк с удельной поверхностью 450 м2/кг, гиперпластификатор Melflux 1641 F.
Алгоритм программы включает основные процедуры: расчета коэффициентов функции отклика, статистической обработки и процедуру визуализации математической модели. Все основные вычисления производятся циклично, что позволяет моментально перестраивать математическую модель, изменяя входные данные. Кроме того, алгоритм включает вспомогательную процедуру, обеспечивающую проверку синтаксической правильности вводимых данных. При допущении ошибок ввода данных программа корректирует действия пользователя по средствам текстового оповещения.
Интерфейс программного продукта реализован в виде логических блоков, позволяющих вводить исходные данные и изменять параметры вывода математической модели в интерактивном режиме (http://www.swsys.ru/uploaded/image/2014-4-dop/10.jpg).
В первом логическом блоке устанавливаются входные факторы эксперимента. В эксперименте варьировались количество вяжущей части, содержание молотого известняка в вяжущей части и количество добавки гиперпластификатора по массе вяжущей части. Блок ввода значений входных факторов представлен в виде таблицы (табл. 1), значения факторов задавались в натуральном виде.
В расчете факторного плана значения уровней входных факторов принимаются в кодированном виде, при этом основной уровень (центр плана) каждого фактора обозначается как «0», а нижний и верхний уровни – «–1» и «+1» соответственно. Пересчет заданных пользователем натуральных значений факторов производится путем линейной интерполяции значений по формуле
 (1)
(1)
где xi – значение i-го фактора в кодированном виде; Xi – значение i-го фактора в натуральном виде; ΔXi – интервал варьирования i-го фактора.
 В эксперименте контролировалась величина предела прочности бетона на сжатие в возрасте 28 суток нормального твердения Rсж, МПа. Для определения воспроизводимости измерений выходного параметра фиксировалось по три параллельных измерения прочности бетона на сжатие. Согласно плану эксперимента было заформовано 10 опытных серий образцов по 3 образца в каждой серии. Рассчитанный трехфакторный план и поля ввода выходных параметров отображаются в виде таблицы (табл. 2) во втором логическом блоке.
В эксперименте контролировалась величина предела прочности бетона на сжатие в возрасте 28 суток нормального твердения Rсж, МПа. Для определения воспроизводимости измерений выходного параметра фиксировалось по три параллельных измерения прочности бетона на сжатие. Согласно плану эксперимента было заформовано 10 опытных серий образцов по 3 образца в каждой серии. Рассчитанный трехфакторный план и поля ввода выходных параметров отображаются в виде таблицы (табл. 2) во втором логическом блоке.
После автоматической проверки введенных данных программа рассчитывает коэффициенты математической модели и выводит функцию отклика в третьем логическом блоке в следующем виде:
Yср = b0+b1*x1+b2*x2+b3*x3+b11*x1^2+b22*x2^2+ +b33*x3^2+b12*x1*x2+b13*x1*x3+b23*x2*x3
y = (47,128)+(14,77)*x1+(1,734)*x2+(5,624)*x3+
+(0,016)*x1^2+(0,471)*x2^2+(0,141)*x3^2+
+2,28*x1*x2+6,01*x1*x3+4,05*x2*x3
После получения математической модели проверяются значимость (отличие от нуля) коэффициентов модели и ее адекватность. Проверка коэффициентов на значимость производится с помощью критерия Стьюдента (t-критерия), который рассчитывается по формуле
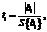 (2)
(2)
где bi – i-й коэффициент математической модели; S{bi} – среднеквадратическое отклонение в определении коэффициентов.
Среднеквадратическое отклонение в определении коэффициентов функции отклика определяется по формуле
 (3)
(3)
где Ci – величины, приведенные для плана B-D13 в таблице 3; Sв2 – дисперсия воспроизводимости в параллельных опытах.
Таблица 3
Величины Ci для плана B-D13
Table 3
The Ci values for plan B-D13
|
b0
|
b1
|
b2
|
b3
|
b11
|
b12
|
b13
|
b22
|
b23
|
b33
|
|
0,868
|
0,159
|
0,159
|
0,159
|
0,594
|
0,226
|
0,226
|
0,594
|
0,226
|
0,594
|
Дисперсия воспроизводимости в параллельных опытах рассчитывается по формуле
 (4)
(4)
где N – количество опытов в плане; m – количество параллельных измерений в каждом опыте; yuj – значение выходного параметра в u-м опыте, j-м параллельном замере;  – среднее значение выходного параметра в u-м опыте.
– среднее значение выходного параметра в u-м опыте.
Расчетное значение t-критерия сравнивается с табличным tтабл для выбранного уровня значимости (как правило, 5 %) и данного числа степеней свободы N(m–1). При ti < tтабл коэффициент bi считается значимым.
Проверка адекватности математической модели производится по критерию Фишера (F-критерий). Для этого вычисляется дисперсия адекватности по формуле
 (5)
(5)
где nз – количество значимых коэффициентов;  – значение отклика, предсказанное по уравнению математической модели.
– значение отклика, предсказанное по уравнению математической модели.
В свою очередь критерий Фишера рассчитывается как отношение
 . (6)
. (6)
Расчетное значение F-критерия сравнивается с табличным Fтабл для выбранного уровня значимости (как правило, 5 %) и чисел степеней свободы N(m–1) и (N–nз). При Fчетвертом логическом блоке (рис. 1).

 Математическая модель прочности мелкозернистого бетона признана адекватной по критерию Фишера (F=3,07 < Fтабл=3,1) и применима для решения рецептурно-технологических задач. Уравнение математической модели представляет собой квадратичную функцию трех переменных:
Математическая модель прочности мелкозернистого бетона признана адекватной по критерию Фишера (F=3,07 < Fтабл=3,1) и применима для решения рецептурно-технологических задач. Уравнение математической модели представляет собой квадратичную функцию трех переменных:
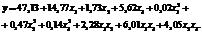
Графическая интерпретация функции трех переменных требует четырехмерного пространства, поэтому для визуального упрощения и удобства работы с математической моделью функцию трех переменных необходимо преобразовать в функцию двух переменных, поочередно принимая константой один из факторов. В пятом логическом блоке программы представлены средства для преобразования уравнения регрессии в функцию двух переменных. Пользователь может установить постоянный фактор и задать его значение (в пределах интервала варьирования) в кодированном и натуральном видах.
В результате преобразования получаются три варианта математической модели: y = f (x2, x3) при x1 = const, y = f (x1, x3) при x2=const и y = f (x1, x2) при x3=const. Для визуализации каждого из трех видов уравнений строится диаграмма линий равного уровня (изолиний), представляющая собой проекции трехмерных поверхностей на плоскости (x2 Å x3), (x1 Å x3) и (x1 Å x2). Таким образом, кривая каждой изолинии строится в координатах (x2, x3), (x1, x3) и (x1, x2), а ее построение производится по квадратичным функциям x2 = f (x3), x1 = f (x3) и x1 = f (x2) соответственно.
В шестом логическом блоке программы представлена интерактивная диаграмма изолиний, позволяющая пользователю снимать координаты факторного поля и значения выходного параметра в режиме реального времени (рис. 2).
Обработка данных планированного экспе- римента завершается процедурой обнаружения экстремума функции отклика. Для определения координат точки экстремума производится автоматическое вычисление первой производной по каждому из значений факторов. Корни полученной системы уравнений представляют собой координаты точки экстремума исследуемого уравнения регрессии:
 (7)
(7)
Экстремум функции отклика математической модели прочности мелкозернистого наполненного бетона обнаружен в пределах варьирования переменных факторов. Значение экстремума составляет 32,7 МПа. Экстремуму функции отклика соответствуют значения факторов: x2 = 5,3 % (процентное содержание известняка в вяжущей части) и x3 = 0,8 % (процентное содержание гиперпластификатора) при x1 = 15 % (общее количество вяжущей части в смеси).
 Программа оснащена дополнительными функциями загрузки/сохранения данных, а также функцией экспорта результатов расчетов в математический пакет Microsoft Excel, где пользователь может осуществить дополнительные построения, например, построить поверхность отклика в трехмерной системе координат (рис. 3а), а также сечения поверхности отклика, позволяющие проанализировать изменения выходного параметра в зависимости от одного переменного фактора (рис. 3б).
Программа оснащена дополнительными функциями загрузки/сохранения данных, а также функцией экспорта результатов расчетов в математический пакет Microsoft Excel, где пользователь может осуществить дополнительные построения, например, построить поверхность отклика в трехмерной системе координат (рис. 3а), а также сечения поверхности отклика, позволяющие проанализировать изменения выходного параметра в зависимости от одного переменного фактора (рис. 3б).
Разработанное программное средство можно применять в любых научно-прикладных задачах по оптимизации свойств объекта исследования, подбора рецептуры и технологических параметров, где используется математическое моделирование методом ортогонального планирования экспериментов.
Литература
1. Белов М.А., Антипов О.Е. Принципы проектирования виртуальной компьютерной лаборатории на основе технологии облачных вычислений // Современные проблемы и пути их решения в науке, транспорте, производстве и образовании: сб. докл. Междунар. конф. Одесса: Изд-во УкрНИИМФ, 2010. С. 27–30.
2. Лесовик В.С. Геоника (геомиметика) как трансдисциплинарное направление исследований // Высшее образование в России. 2014. № 3. С. 77–83.
3. Соловов А.В. Виртуальные учебные лаборатории в инженерном образовании // Индустрия образования: сб. статей. Вып. 2. М.: Изд-во МГИУ, 2002. С. 386–392.
4. Норенков И.П., Зимин А.М. Информационные технологии в образовании. М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. 352 с.
5. Белов В.В., Образцов И.В. Виртуализация физических процессов в теории и практике строительного образования // Теория и практика повышения эффективности строительных материалов: матер. V Всерос. конф. студ., аспирантов и молодых ученых. Пенза: Изд-во ПГУАС, 2010. С. 186–189.
6. Афанасьев В.О., Бровкин А.Г. Исследования и разработка системы интерактивного наблюдения индуцированной виртуальной среды (системы виртуального присутствия) // Космонавтика и ракетостроение. 2001. № 20. С. 19–21.
7. Колганов Д.А. Нереальная физика. Тестирование NVIDIA PhysX на конфигурации SLI Multi-Card // Игромания. 2010. Февраль. С. 162–164.
8. Zhang G., Torquato S. Precise algorithm to generate random sequential addition of hard hyperspheres at saturation. Physical review, E 88, 2013, pp. 053312-1-9.
9. Баженов Ю.М., Демьянова В.С., Калашников В.И. Модифицированные высококачественные бетоны: науч. издание. М.: Изд-во Ассоциации строительных вузов, 2006. 368 с.
10. Белов В.В., Образцов И.В., Реунов А.Г., Смирнов М.А. Компьютерный метод расчета зернового состава заполнителя строительного композита // Актуальные проблемы строительства и строительной индустрии: сб. матер. Х Междунар. науч.-технич. конф. Тула, 2009. С. 6–7.
References
1. Belov M.A., Antipov O.E. Design principles for virtual computer laboratory on the basis of cloud computing
technology. Sovremennye problemy i puti ikh resheniya v nauke, transporte, proizvodstve i obrazovanii: sb. dokl.
Mezhdunar. konf. [Proc. of the Int. Conf. Modern Problems and their Solving in Science, Transport, Production and
Education]. Odessa, UkrNIIMF, 2010, pp. 27–30 (in Russ.).
2. Lesovik V.S. Geonica (geodaetica) as a transdisciplinary field of research. Vyshee obrazovanie v Rossii [Higher
Education in Russia]. 2014, no. 3, pp. 77–83 (in Russ.).
3. Solovov A.V. Virtual training laboratories in engineering education. Industriya obrazovaniya: sb. statey [Edu-cation Industry: Proc.]. Iss. 2. Moscow, Moscow St. Industrial Univ. Publ., 2002, pp. 386–392 (in Russ.).
4. Norenkov I.P., Zimin A.M. Informatsionnye tekhnologii v obrazovanii [Information Technologies in Educa-tion]. Moscow, MSTU Publ., 2004, 352 p.
5. Belov V.V., Obraztsov I.V. Virtualization of physical processes in the theory and practice of construction edu-cation. Teoriya i praktika povysheniya effektivnosti stroitelnykh materialov: materialy V Vseros. konf. stud., asp irantov
i molodykh uchenykh [Proc. 5th All-Russian Conf. The Theory and Practice of Increasing Efficiency of Constructional
Materials]. Penza, Penza St. Univ. Architecture and Construction Publ., 2010, pp. 186–189 (in Russ.).
6. Afanasyev V.O., Brovkin A.G. Research and development of a system for interactive monitoring induced vir-tual environment (virtual presence). Kosmonavtika i raketostroenie [Astronautics and Rocket Production]. 2001,
no. 20, pp. 19–21 (in Russ.).
7. Kolganov D.A. Unrealistic physics. Testing NVIDIA PhysX in SLI configuration Multi-Card. Igromaniya.
2010, February, pp. 162–164 (in Russ.).
8. Zhang G., Torquato S. Precise algorithm to generate random sequential addition of hard hyperspheres at satura-tion. Physical Review. E 88. 2013, pp. 053312-1-9.
9. Bazhenov Yu.M., Demyanova V.S., Kalashnikov V.I. Modifitsirovannye vysokokachestvennye betony:
nauchnoe izdanie [Modified High-Quality Concretes: Scientific Publication]. Moscow, Assotsiatsiya Stroitelnykh
Vuzov Publ., 2006, 368 p.
10. Belov V.V., Obraztsov I.V., Reunov A.G., Smirnov M.A. Computer calculation method of the grain structure
of a filler composite construction. Aktualnye problemy stroitelstva i stroit. industrii: sb. materialov X Mezhdunar.
nauch.-tekhnich. konf. [Proc. 10th Int. Science and Technical Conf. Important Building and Building Industry Prob-lems]. Tula, 2009, pp. 6–7 (in Russ.).
 (1)
(1)
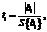 (2)
(2) (3)
(3) (4)
(4) – среднее значение выходного параметра в u-м опыте.
– среднее значение выходного параметра в u-м опыте. (5)
(5) – значение отклика, предсказанное по уравнению математической модели.
– значение отклика, предсказанное по уравнению математической модели. . (6)
. (6)

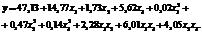
 (7)
(7)
