Задача расчета течений со свободной поверхностью рассматривалась многими авторами, что говорит о ее практической значимости. Специфика задачи связана с наличием области контакта двух сред – жидкости и газа. Чаще практический интерес представляет именно состояние жидкости в области контакта [1]. Сегодня существует целый ряд универсальных программных комплексов, обеспечивающих решение подобных задач: FLOW-3D [2, 3], SolidWorks/FloWorks [4], ANSYS [5], FlowVision HPC [6], OpenFOAM [7]. Есть примеры решения задачи на графическом процессоре [8], что весьма интересно и перспективно, поскольку не требуется перекачка больших объемов данных на каждом шаге решения на видеокарту. Существуют и разработки (например [9]), основанные на оригинальных методиках. Рассмотрим результаты, полученные при решении задачи анимации движущегося объекта в реальном времени, что определяет ограничения на время ее решения.
Движущийся объект рассматривается в трехмерном пространстве, в соответствии с этим вектор скорости движения объекта v содержит три компоненты: vx, vy, vz. Центр системы координат лежит в геометрическом центре объекта. Система координат связана с объектом. Ориентация осей координат показана на рисунке 1.
 Объект может вращаться вокруг осей Z и Y. Вращение вокруг оси X не оказывает существенного влияния на формирование искомых возмущений (хотя это непринципиально и легко может быть введено в рассмотрение). Объект движется в районе поверхности в земных условиях. Параметры движения объекта заданы (компоненты скорости, угловых скоростей вращения относительно осей (wx, wy, wz), причем wx = 0, единичный вектор гравитации (G = (gx, gy, gz)) c нормированными компонентами проекции силы тяжести в выбранной системе координат. Положим, что задана также текущая глубина погружения геометрического центра объекта H, тогда входную компоненту скорости vz можно принять равной 0. Предполагается, что объект движется в водной среде. Требуется рассчитать поверхностные возмущения от движения объекта в реальном времени.
Объект может вращаться вокруг осей Z и Y. Вращение вокруг оси X не оказывает существенного влияния на формирование искомых возмущений (хотя это непринципиально и легко может быть введено в рассмотрение). Объект движется в районе поверхности в земных условиях. Параметры движения объекта заданы (компоненты скорости, угловых скоростей вращения относительно осей (wx, wy, wz), причем wx = 0, единичный вектор гравитации (G = (gx, gy, gz)) c нормированными компонентами проекции силы тяжести в выбранной системе координат. Положим, что задана также текущая глубина погружения геометрического центра объекта H, тогда входную компоненту скорости vz можно принять равной 0. Предполагается, что объект движется в водной среде. Требуется рассчитать поверхностные возмущения от движения объекта в реальном времени.
Теоретические посылки
Решение поставленной задачи базируется на использовании уравнений Навье–Стокса:
 , (1)
, (1)
 , (2)
, (2)
 , (3)
, (3)
где X, Y, Z – проекции массовых сил (силы тяжести); r – плотность жидкости (воды); m – вязкость жидкости; p – давление. Используя конечно-разностные аналоги (1)–(3) для оценки производных на некоторой сетке и имея оценку поля давления, можно получить на очередном шаге оценки скоростей. Поскольку неизвестными являются четыре величины vx, vy, vz и p, для замыкания системы традиционно используется еще уравнение неразрывности (при условии постоянства плотности жидкости):
 (4)
(4)
Порядок решения
Решение выполняется на равномерной сетке размерностью nx, ny, nz.
1. Определение параметров сетки.
На сетке задается 3D-аппроксимация объекта. Сетка несколько расширяется, чтобы можно было видеть состояние поверхности в окрестности объекта. Конечно, вычислительные затраты при этом растут, что ограничивает возможности увеличения сетки. Сетка в процессе расчета не модифицируется. Часто рассматриваются подходы, связанные с локальным измельчением сетки [1, 2, 9], но это требует дополнительных затрат. Каждый из кубиков сетки лежит в свободной области, частично принадлежит свободному объему (находится вне объекта) или полностью находится внутри объекта (внутренние кубики). Для кубиков на границе объекта определяются площади усеченных граней, соответствующие свободному объему, и сам свободный объем. Кубик полагается внутренним, если более половины его объема лежит внутри объекта. Это устанавливается на предварительном этапе подготовки задачи к решению.
2. Формирование среды в кубиках сетки.
Для описания состояния кубика используется технология, похожая на VOF [2, 3, 5–7].
2.1. Строится плоскость невозмущенной поверхности жидкости с нормалью, равной вектору гравитации G = (gx, gy, gz): gxx+gyy+gzz+H=0, где H – текущая величина заглубления объекта.
2.2. Для всех кубиков сетки определяется расстояние центра кубика до невозмущенной поверхности r:
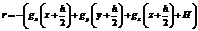 , где x, y, z – координаты начального угла кубика (минимальные координаты кубика); h – шаг сетки.
, где x, y, z – координаты начального угла кубика (минимальные координаты кубика); h – шаг сетки.
Кубик классифицируется относительно невозмущенной поверхности. Если r ³ h/2, то весь объем кубика расположен выше невозмущенной поверхности, в противном случае кубик имеет некоторый объем жидкости.
Кубик классифицируется относительно возмущенной поверхности. Допустим, существует двумерный массив ординат возмущенной поверхности S(nx, ny), каждый элемент которого содержит ординату отклонения от невозмущенной поверхности в данной точке.
Рассчитывается величина заглубления кубика rk*. Если сверху по Z нет кубиков, попадающих в объем тела, rk* = r – S(i, j). Если они есть, то rk* = r. При rk*³h/2 средняя точка кубика выше возмущенной поверхности не менее, чем на половину высоты кубика (в кубике только воздух). При rk*£–h/2 средняя точка кубика ниже возмущенной поверхности не менее, чем на половину его высоты – в кубике вода. Если –h/2£rk*£h/2, кубик заполнен жидкостью частично. По результатам классификации устанавливается гидростатическое давление в кубике. Удобно нормировать давление на произведение плотности на ускорение силы тяжести, в результате чего давление становится равным высоте столба жидкости в кубике. Классификация выполняется только для кубиков, лежащих вне объема тела. Полагается, что кубики в объеме тела содержат только воздух. Давление в кубиках с воздухом принимается равным нулю.
3. Формирование (корректировка) оценки поля скоростей.
Внутренние кубики и кубики с воздухом не рассматриваются. При этом линейные скорости по X, Y и Z модифицируются при наличии вращений относительно осей Z и Y. Скорости вводятся с коэффициентом релаксации (kv = 0,5), например, для скорости по X  .
.
Скорости по Z не оцениваются, так как перемещение по этой координате на каждом шаге определяется величиной заглубления объекта. Для кубиков неполного объема по границе объекта оценки скоростей не формируются.
4. Вычисление поля скоростей.
Вычисления производятся для кубиков, заполненных полностью или частично жидкостью, вычисляются также компоненты скоростей для тех граней кубиков с воздухом, которые имеют смежные кубики, заполненные жидкостью. При этом используются конечно-разностные аналоги уравнений Навье–Стокса. Скорости на гранях кубиков, лежащих на границе расчетной области, не вычисляемые непосредственно, приравниваются к вычисленным значениям по соответствующей координате (открытые границы расчетной области). Эффект прилипания поверхностного слоя жидкости к поверхности объекта имитируется занулением скоростей вдоль поверхности объекта. Кроме того, задаются условия непротекания.
5. Уточнение поля давления.
На каждом шаге по времени должно выполняться уравнение неразрывности в каждом кубике. Приближение к выполнению этого условия реализуется на основе уточнения поля давления решением уравнения Пуассона. Рассмотрим эту методику, следуя [1]. Введем обозначения граней кубика и скоростей через грани (рис. 2).
 Под гранью здесь будем понимать площадь смоченной поверхности грани кубика. Для поверхностных кубиков она чаще всего меньше полной площади грани. Левая грань (лежащая в плоскости Z0Y) и соответствующая скорость потока через нее обозначены sw и vw. Правая грань и скорость потока через нее обозначены se и ve. Ближняя грань по Y и соответствующая скорость обозначены sn и vn. Задняя грань (по Y) имеет обозначения ss и vs, нижняя – sb и vb, верхняя– st и vt. С использованием введенного обозначения скоростей конечно-разностный аналог (1) выглядит следующим образом:
Под гранью здесь будем понимать площадь смоченной поверхности грани кубика. Для поверхностных кубиков она чаще всего меньше полной площади грани. Левая грань (лежащая в плоскости Z0Y) и соответствующая скорость потока через нее обозначены sw и vw. Правая грань и скорость потока через нее обозначены se и ve. Ближняя грань по Y и соответствующая скорость обозначены sn и vn. Задняя грань (по Y) имеет обозначения ss и vs, нижняя – sb и vb, верхняя– st и vt. С использованием введенного обозначения скоростей конечно-разностный аналог (1) выглядит следующим образом:
 , (5)
, (5)
где Tx – конечно-разностный аналог величины
 ; (6)
; (6)
индекс (n+1) обозначает величину скорости на (n+1)-м шаге по времени; Px– – давление в предыдущем (слева) по X кубике. Для правой грани кубика
 . (7)
. (7)
Здесь X+, Px+, Tx+ – проекция массовых сил, давление и конечно-разностный аналог величины (6) для следующего по X кубика (правого).
Для проекций (2) и (3) также можно записать соответствующие выражения.
Уравнение неразрывности (4) является формой закона сохранения массы в гидродинамике. С учетом непостоянства площади грани истечения (4) корректно писать в виде
 . (8)
. (8)
Здесь каждая из производных выражает изменение объема жидкости, проходящей через кубик, по каждой из координат.
Конечно-разностный аналог (8) на данном шаге по времени обозначим D: D = 1/n(seve – swvw + + snvn – ssvs + stvt – sbvb).
В принятых обозначениях запишем конечно-разностный аналог (8) для (n+1)-го шага по времени:

Поскольку должно выполняться условие D(n+1)=0, решаем это уравнение относительно P и получаем выражение для уточнения давления в кубике на каждом шаге:
 . (9)
. (9)
Здесь использованы следующие обозначения:
Sc = (seX+ – swX + snY+ – ssY + stZ+– sbZ),
Sp = (se Px+ + sw Px– + snPy+ + ss Py– + stPz++ sb Pz–),
Sd = (se Tx+ – sw Tx + snTy+ – ss Ty + stTz+– sb Tz).
Если кубик имеет полные грани (погруженные кубики, не усеченные телом объекта), то все поверхности равны и выражение (9) упрощается:
 ,
,
где использованы следующие обозначения: Ps = Px+ + Px– + Py+ + Py– + Pz++ Pz–, Ts = Tx+ – Tx + + Ty+ – Ty + Tz+– Tz.
Уравнение Пуассона решается методом релаксации, то есть последовательным пересчетом по всему полю давлений. Полученные уточненные оценки давления в кубиках P* вводятся с коэффициентом релаксации k = 0,1, то есть
P(n+1)= kP*+ (1–k) P(n). (10)
6. Уточнение поля скоростей.
После уточнения поля давлений следует уточнить оценки поля скоростей. Для этого можно использовать алгоритм, применяемый на шаге 4, либо попытаться сэкономить время, уточнив оценки скоростей сразу после уточнения оценки величины давления в кубике на шаге 5. Из (5) выразим приращение скорости при уточнении оценки скорости на шаге для каждой координаты (опуская индекс грани и шага):  .
.
После уточнения давления в данной ячейке на DP новая оценка скорости выражается следующим образом:
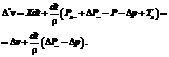 (11)
(11)


 Параметр Dv в (11) представляет собой уточнение оценки скорости, полученное на шаге 4 и уже включенное в оценку скорости. Второе слагаемое – это добавка к оценке скорости, связанная с коррекцией поля давления, причем первая дельта давления в скобках – уже вычисленная на предыдущем шаге уточненная оценка давления, а Dp – корректор давления на данном шаге. Учитывая, что пересчет давления выполняется с релаксацией (10), приращение Dp следует вычислять как Dp = = (1–k) (P* – P(n)), где P* – P(n) – пересчитанная величина (9) и старая корректируемая оценка давления в кубике. Значение Dp следует сохранить до следующего шага по пространству по соответствующей координате для использования в качестве DP– в (11).
Параметр Dv в (11) представляет собой уточнение оценки скорости, полученное на шаге 4 и уже включенное в оценку скорости. Второе слагаемое – это добавка к оценке скорости, связанная с коррекцией поля давления, причем первая дельта давления в скобках – уже вычисленная на предыдущем шаге уточненная оценка давления, а Dp – корректор давления на данном шаге. Учитывая, что пересчет давления выполняется с релаксацией (10), приращение Dp следует вычислять как Dp = = (1–k) (P* – P(n)), где P* – P(n) – пересчитанная величина (9) и старая корректируемая оценка давления в кубике. Значение Dp следует сохранить до следующего шага по пространству по соответствующей координате для использования в качестве DP– в (11).
7. Реализация перетоков жидкости.
Описанные шаги позволяют ответить на вопрос о том, каким будет поле давлений при движении данного объекта с данной скоростью, то есть рассчитать статическое поле давлений, соответствующее заданным параметрам движения объекта. При неизменных параметрах движения получим статичную или почти статичную картинку.
Чтобы оживить картинку, следует реализовать перемещение жидкости – перетоки (похожий прием используется в [9]). В данном случае (расчет поверхностных возмущений и дефицит времени решения) можно ограничиться реализацией перемещения жидкости только в поверхностном слое. В целях экономии ресурсов задача решается приближенно в предположении истечения только через полную грань. По каждой координате рассчитывается оценка изменения объема жидкости в кубике: DVx=(vw–ve)Sdt, DVy=(vs–vn)Sdt, DVz= =(vb–vt)Sdt.
Сумма этих величин дает приращение жидкости в кубике, в результате чего он может изменить свое состояние (степень заполнения жидкостью).
8. Формирование (уточнение) ординат поверхности.
В результате выполнения этапов 2–7 расчета получена уточненная оценка поля давления на данном шаге, которая, вероятно, имеет отклонение от поля, сформированного на шаге 2. Суммарная величина этих отклонений, рассчитанная в кубиках для данной пары координат (x, y), при изменении третьей (z) от поверхности в глубину дает корректирующую поправку ординаты поверхности S(i, j).
Этим завершается шаг алгоритма (пункты 2–8).
Полученные результаты
Задача решалась на сетке с шагом 0,5 м. В качестве модельных рассматривались условные объекты, состоящие из хорошо формализуемых фрагментов поверхностей (см. рис. 3–5). Заглубление центра дано относительно невозмущенной поверхности. Время выполнения шага указано для процессора i5-3570 с включением затрат времени на формирование самой картинки. Размерность сетки полная (с учетом воздушных кубиков).
На основании изложенного можно сделать следующие выводы. В целом предложенный подход позволяет рассчитать приемлемую картину возмущений поверхности, вызванную движением объекта. Определенная неадекватность картины возмущений, видимо, связана с нарушением предположения о ламинарности течения, отсутствием обработки турбулентности и разрывов поверхности (то есть с нарушением выполнения уравнения неразрывности), что, собственно, и определяет введенное ограничение скорости движения объекта. Однако по постановке задача решается в условиях дефицита времени и определенные отклонения качества в этом случае можно рассматривать как допустимые. Конечно, подобным образом можно оценить и обтекание объекта жидкостью при его движении в глубине, что проще (быстрее), так как не требуется обработка границы раздела двух сред – жидкости и воздуха.
Литература
1. Computation of Free-Surface Flows Using Finite-Volume Method. Milovan Perić URL: http://congress.cimne.com/cfsi/frontal/doc/ppt/16.pdf (дата обращения: 19.02.2015).
2. Моделирование FLOW-3D. URL: http://www.vevivi.ru/ best/Modelirovanie-FLOW-3D-ref194601.html (дата обращения: 16.02.2015).
3. Free Surface Fluid Flow. URL: http://www.flow3d.com/ home/resources/cfd-101/free-surface-fluid-flow (дата обращения: 16.02.2015).
4. Ушаков В. Анализ обтекания тел с отрывом потока в системе SolidWorks/FloWorks. URL: http://www.cadcamcae.lv/ hot/obtekanie.pdf (дата обращения: 16.02.2015).
5. Introduction of Multiphase Flow. URL: http://www.ansys. com/staticassets/ANSYS/staticassets/resourcelibrary/presentation/korea-2014ugm-multiphase-flow-modeling.pdf (дата обращения: 16.02.2015).
6. Аксенов А.А., Дядькин А.А., Сушко Г.Б., Харчен- ко С.А. Развитие параллельной версии FlowVision HPC. URL: http://www.tesis.com.ru/infocenter/downloads/flowvision/fv_es09_tes2.pdf (дата обращения: 19.02.2015).
7. Жайнаков А.Ж., Курбаналиев А.Ы. Трехмерное моделирование потока жидкости со свободной границей методом объема жидкости. URL: http://arch.kyrlibnet.kg/uploads/KRSUJAYNAKOVA.J.2013-1.pdf (дата обращения: 19.02.2015).
8. Гугушвили И.В., Евстигнеев Н.М. Некоторые результаты для различных методов моделирования несжимаемой гидродинамики свободной поверхностью на графических процессорах. 2010. URL: http://www.scientific-notes.ru/pdf/017-02.pdf (дата обращения: 17.02.2015).
9. Никитин К.Д. Реалистичное моделирование свободной водной поверхности на адаптивных сетках типа «восьмеричное дерево». URL: http://ntv.ifmo.ru/file/article/401.pdf (дата обращения: 16.02.2015).
10. Поттер Д. Вычислительные методы в физике. М.: Мир, 1975. 392 с.

 , (1)
, (1) , (2)
, (2) , (3)
, (3) (4)
(4)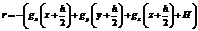 , где x, y, z – координаты начального угла кубика (минимальные координаты кубика); h – шаг сетки.
, где x, y, z – координаты начального угла кубика (минимальные координаты кубика); h – шаг сетки. .
.
 , (5)
, (5) ; (6)
; (6) . (7)
. (7) . (8)
. (8)
 . (9)
. (9) ,
, .
.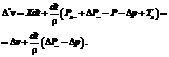 (11)
(11)


