Создание компьютерных систем (КС) с десятками и сотнями тысяч компьютерных компонентов [1] актуализировало проблему разработки эффективных методов управления их ресурсами. При этом в качестве критерия эффективности обычно рассматривается требование минимизации используемых ресурсов КС при удовлетворении требований к выполняемому в общем случае потоку программ. Для КС общего назначения такими требованиями являются достижение максимальной реальной производительности (среднего количества программ, выполняемых в единицу времени). Для кластеров и многоядерных компьютеров критерий эффективности – это достижение заданного (минимального в теоретическом плане) времени выполнения параллельной программы при условии использования минимального количества компонентов КС.
В силу примитивного характера средств управления КС в настоящее время программист, используя, например, кластер и MPI, должен сам определить оптимальную степень распараллеливания (зернистость) и необходимое количество компонентов КС, затем распределить процессы таким образом, чтобы достигалось желаемое время выполнения параллельной программы. В результате, как показывает практика, даже для этой простой модели параллелизма, применяемой в MPI и исключающей возможность порождения процессов (имеется в виду MPI-1), процессоры или компьютеры кластера используются всего на 10–15 %. Аналогичное состояние в решении проблемы управления наблюдается в обобществляемых или слабо связанных в отличие от кластеров КС, называемых GRID, CLOUDS, то есть в глобальных компьютерных сетях. Управление подобными КС усложняется вследствие неоднородности их компонентов и большой удаленности выделяемых ресурсов, необходимости объективного учета оплаты за используемые пользователями ресурсы. Сложность проблемы создания эффективных средств управления большими КС заключается в том, что порождение процессов имеет случайный характер, то же самое относится к их сложности и, следовательно, к генерируемым процессами требованиям к различным ресурсам КС [2–6]. Поэтому в реализации на КС созданных нами высокоуровневых языков параллель- ного программирования (языка функционального параллельного программирования [7] и языка граф-схемного потокового программирования [8]) мы используем адаптивные методы для управления процессами и ресурсами в КС [5, 6]. Их главная особенность заключается в измерении и прогнозировании загруженности ресурсов КС (процессоров, памяти, каналов, периферийных устройств) и построении на этой основе системы решающих правил, позволяющих в динамике регулировать объем ресурсов, необходимый для эффективного выполнения программ и процессов. В статье приведены результаты экспериментального исследования методов прогнозирования загруженности процессоров КС – основного ресурса, по эффективности использования которого обычно определяют реальную производительность КС. Кроме того, дан сравнительный анализ полученных результатов, подтверждающий тезис о возможности с достаточно высокой точностью прогнозировать загруженность процессоров КС. Отметим, что у этого результата есть и другое, самостоятельное значение, показывающее, что случайные процессы загруженности, в частности, загруженности процессоров и компьютеров КС, имеют вполне закономерную стохастическую природу.
Экспериментальное исследование методов прогнозирования загруженности процессоров
Приведем результаты выполненного авторами экспериментального исследования прогнозирования загруженности процессора компьютера по данным ее измерения стандартными средствами ОС сегодняшних компьютеров. При этом для обеспечения большой точности измеряемые счетчиками значения загруженности представляют собой высокочастотный процесс, а интервалы измерений находятся в пре- делах нескольких микросекунд. Поэтому предска- зывать изменение загруженности с достаточной точностью можно, лишь применяя соответствующие методы сглаживания процесса или подавления его высокочастотной составляющей.
 Подобные методы давно используются в радиолокации и хорошо исследованы (см., например, [9]). Эти методы, реализованные как фильтры, мы используем в наших экспериментальных исследованиях прогнозирования изменения загруженности компьютеров и КС. В качестве объекта, для которого исследовалась проблема измерения и прогнозирования загруженности, использовался персональный компьютер с быстродействием 4´109 оп./сек. и объемом ОП, равным 4 Гб. Отметим, что современные кластеры строятся с такими же характеристиками компонентов.
Подобные методы давно используются в радиолокации и хорошо исследованы (см., например, [9]). Эти методы, реализованные как фильтры, мы используем в наших экспериментальных исследованиях прогнозирования изменения загруженности компьютеров и КС. В качестве объекта, для которого исследовалась проблема измерения и прогнозирования загруженности, использовался персональный компьютер с быстродействием 4´109 оп./сек. и объемом ОП, равным 4 Гб. Отметим, что современные кластеры строятся с такими же характеристиками компонентов.
Для получения достоверных результатов применялся широкий круг хорошо известных приложений, таких как Microsoft Visual Studio, MathСad, MSOffice, SQL Server, браузеры и др.
Для сбора и обработки статистических данных было разработано специальное приложение, позволяющее варьировать дискретность измерений процесса загруженности процессора компьютера, метод сглаживания и метод прогнозирования изменения загруженности.
Прогноз изменений параметров загруженности есть смысл делать на 0,5–1 сек. вперед из-за нестационарности и непредсказуемости графиков загруженности процессора. Предсказываемое значение загруженности  на момент будущего представляется как константа, равная полученному сглаженному значению
на момент будущего представляется как константа, равная полученному сглаженному значению  в текущий момент времени:
в текущий момент времени:
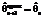 . (1)
. (1)
Все рассмотренные методы сглаживания были экспериментально исследованы с помощью программ MathCAD. Для приведенной в статье реализации процесса загруженности вычислялись средняя и максимальная ошибки предсказания загруженности процессора и их дисперсии на 0,5 сек. вперед.
Экстраполятор на основе экспоненциального сглаживания. Экспоненциальное сглаживание – один из простейших и распространенных приемов выравнивания временного ряда. Экспоненциальное сглаживание можно представить как фильтр, на вход которого последовательно поступают члены исходного ряда, а на выходе формируются текущие значения экспоненциальной средней.
При экспоненциальном сглаживании предыдущие значения параметров учитываются с убывающими по экспоненциальному закону весами.
В простейшем случае для нахождения очередного сглаженного значения используются только текущее измерение и предыдущее сглаженное значение. Формула прогнозирования имеет вид (в соответствии с (1)): 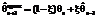 , где qn – измеренное значение параметра в n-й момент времени;
, где qn – измеренное значение параметра в n-й момент времени;  – сглаженное значение параметра в n-й момент времени; x – постоянная величина, имеющая смысл коэффициента сглаживания.
– сглаженное значение параметра в n-й момент времени; x – постоянная величина, имеющая смысл коэффициента сглаживания.
На рисунке 1 приведен пример прогнозирования на основе экспоненциального сглаживания загруженности процессора (X – график загруженности процессора, Exp – экспоненциальное сглаживание X). На этом рисунке и рисунке 2 промежуток между съемами данных принят равным 0,5 сек., количество измерений t =1200, прогноз приводится на 1 шаг вперед.
В данном методе ошибки предсказания загруженности в первую очередь зависят от параметра x. Средняя ошибка прогнозирования определяется по формуле  , а максимальная ошибка прогнозирования по формуле
, а максимальная ошибка прогнозирования по формуле 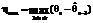 .
.
Значения ошибки прогнозирования в зависимости от параметра x приведены в таблице 1.
Экстраполятор с равномерным окном. При экстраполяции с равномерным окном происходит усреднение по T предыдущим измерениям с равными весами. Формула экстраполятора с равномерным окном имеет следующий вид:  , где qn-k – измеренное значение параметра в (n–k)-й момент времени, k≥1;
, где qn-k – измеренное значение параметра в (n–k)-й момент времени, k≥1;  – сглаженное значение параметра в n-й момент времени; T – ширина окна (количество точек в окне).
– сглаженное значение параметра в n-й момент времени; T – ширина окна (количество точек в окне).
Таблица 1
Зависимость ошибки прогнозирования от параметра x
Table 1
A misprediction depending on x parameter
|
Пара- метр x
|
Средняя ошибка прогнозирования
|
Дисперсия ошибки
|
Максимальная ошибка прогнозирования
|
|
0,1
|
0,094
|
8,7´10-3
|
0,49
|
|
0,2
|
0,087
|
7,1´10-3
|
0,473
|
|
0,3
|
0,085
|
6,6´10-3
|
0,462
|
|
0,4
|
0,083
|
6,3´10-3
|
0,454
|
|
0,5
|
0,08
|
6,3´10-3
|
0,45
|
|
0,6
|
0,08
|
6,4´10-3
|
0,449
|
|
0,7
|
0,081
|
6,6´10-3
|
0,45
|
Рассматривается одношаговый экстраполятор с равномерным окном. Экспериментальные данные ошибок прогнозирования загруженности процессора в зависимости от параметра ширины окна T для этого метода сглаживания приведены в таблице 2.
Таблица 2
Экспериментальные данные ошибок прогнозирования
Table 2
Misprediction experimental data
|
Параметр
|
Средняя ошибка прогнозирования
|
Дисперсия ошибки
|
Максимальная ошибка прогнозирования
|
|
2
|
0,093
|
8,7´10-3
|
0,533
|
|
3
|
0,093
|
8,7´10-3
|
0,533
|
|
5
|
0,092
|
8,5´10-3
|
0,472
|
|
10
|
0,093
|
9,8´10-3
|
0,497
|
|
15
|
0,093
|
0,011
|
0,529
|
|
20
|
0,094
|
0,012
|
0,545
|
|
25
|
0,095
|
0,012
|
0,556
|
|
30
|
0,114
|
0,013
|
0,565
|
|
35
|
0,117
|
0,014
|
0,567
|
|
40
|
0,12
|
0,014
|
0,572
|
|
45
|
0,123
|
0,015
|
0,578
|
|
50
|
0,125
|
0,016
|
0,578
|
Экстраполятор с подбором весовых коэффициентов. При экстраполяции с подбором весовых коэффициентов происходит усреднение по T предыдущим измерениям с различными весами. Формула экстраполятора с подбором весовых коэффициентов имеет следующий вид:  где qn-i – измеренное значение параметра в (n–i)-й момент времени;
где qn-i – измеренное значение параметра в (n–i)-й момент времени;  – сглаженное значение параметра в n-й момент; T – ширина окна; ci – вес qn-i-го измерения.
– сглаженное значение параметра в n-й момент; T – ширина окна; ci – вес qn-i-го измерения.
Вес произвольного i-го измерения ci, в первую очередь, определяется коэффициентом убывания весов s и вычисляется по формуле  , где
, где 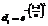 .
.
Рассматривается одношаговый экстраполятор с подбором весовых коэффициентов. Средняя и максимальная ошибки прогнозирования загруженности в зависимости от параметров T и s для этого метода сглаживания приведены в таблице 3.
Таблица 3
Средняя и максимальная ошибки прогнозирования
Table 3
An average and maximal misprediction
|
Параметр
|
Средняя ошибка прогнозирования
|
Дисперсия ошибки
|
Максимальная ошибка прогнозирования
|
|
|
T
|
|
2
|
3
|
0,093
|
8,6´10-3
|
0,525
|
|
10
|
0,092
|
8,5´10-3
|
0,503
|
|
20
|
0,092
|
8,5´10-3
|
0,503
|
|
30
|
0,093
|
8,5´10-3
|
0,503
|
|
40
|
0,093
|
8,5´10-3
|
0,503
|
|
4
|
3
|
0,093
|
8,6´10-3
|
0,531
|
|
10
|
0,092
|
8,4´10-3
|
0,464
|
|
30
|
0,092
|
8,4´10-3
|
0,464
|
|
40
|
0,092
|
8,4´10-3
|
0,464
|
|
8
|
3
|
0,093
|
8,7´10-3
|
0,533
|
|
10
|
0,095
|
9´10-3
|
0,482
|
|
20
|
0,096
|
9,1´10-3
|
0,484
|
|
30
|
0,096
|
9,1´10-3
|
0,484
|
|
40
|
0,096
|
9,1´10-3
|
0,484
|
|
15
|
3
|
0,093
|
8,7´10-3
|
0,533
|
|
10
|
0,098
|
9,5´10-3
|
0,489
|
|
30
|
0,102
|
0,1
|
0,527
|
|
40
|
0,091
|
0,1
|
0,527
|
|
30
|
3
|
0,093
|
8,7´10-3
|
0,533
|
|
10
|
0,099
|
9,8´10-3
|
0,495
|
|
20
|
0,106
|
0,011
|
0,539
|
|
30
|
0,109
|
0,012
|
0,554
|
|
40
|
0,111
|
0,012
|
0,558
|
|
50
|
3
|
0,093
|
8,7´10-3
|
0,533
|
|
20
|
0,107
|
0,011
|
0,543
|
|
40
|
0,116
|
0,014
|
0,567
|
|
50
|
0,119
|
0,014
|
0,572
|
Медианный фильтр. Медианные фильтры достаточно часто применяются на практике для предварительной обработки цифровых данных как альтернатива средним арифметическим значениям отсчетов в оценке выборочных средних значений. Медианой числовой последовательности x1, x2, …, xn при нечетном n является средний по значению член ряда, получающегося при упорядочивании этой последовательности по возрастанию (или убыванию). Для четных n медиану обычно определяют как среднее арифметическое двух средних отсчетов упорядоченной последовательности.
 Медианный фильтр представляет собой оконный фильтр, последовательно скользящий по изменяющимся значениям сигнала и возвращающий на каждом шаге одно из значений, попавших в окно (апертуру) фильтра. Выходной сигнал yk скользящего медианного фильтра шириной 2n+1 для текущего отсчета k формируется из входного временного ряда …, xk-1, xk, xk+1, … в соответствии с формулой yk = = med(xk-n, xk-n-1, …, xk-1, xk, xk+1, …, xk+n-1, xk+n), где med(z(1), …, z(m), …, z(2n+1)) = z(n+1), z(m) – элементы вариационного ряда, ранжированные в порядке возрастания значений, z(1)£z(2)£¼£z(2n+1). Медианная фильтрация реализуется в виде процедуры локальной обработки отсчетов в скользящем окне, которое включает определенное число отсчетов сигнала. Для каждого положения окна выделенные в нем отсчеты ранжируются по возрастанию или убыванию значений. Средний по своему положению отсчет в ранжированном списке называется медианой рассматриваемой группы отсчетов. Им заменяется центральный отсчет в окне для обрабатываемого сигнала. В силу этого медианный фильтр относится к числу нелинейных фильтров, заменяющих медианным значением аномальные точки и выбросы независимо от их амплитудных значений, и является устойчивым по определению, способным аннулировать даже бесконечно большие отсчеты.
Медианный фильтр представляет собой оконный фильтр, последовательно скользящий по изменяющимся значениям сигнала и возвращающий на каждом шаге одно из значений, попавших в окно (апертуру) фильтра. Выходной сигнал yk скользящего медианного фильтра шириной 2n+1 для текущего отсчета k формируется из входного временного ряда …, xk-1, xk, xk+1, … в соответствии с формулой yk = = med(xk-n, xk-n-1, …, xk-1, xk, xk+1, …, xk+n-1, xk+n), где med(z(1), …, z(m), …, z(2n+1)) = z(n+1), z(m) – элементы вариационного ряда, ранжированные в порядке возрастания значений, z(1)£z(2)£¼£z(2n+1). Медианная фильтрация реализуется в виде процедуры локальной обработки отсчетов в скользящем окне, которое включает определенное число отсчетов сигнала. Для каждого положения окна выделенные в нем отсчеты ранжируются по возрастанию или убыванию значений. Средний по своему положению отсчет в ранжированном списке называется медианой рассматриваемой группы отсчетов. Им заменяется центральный отсчет в окне для обрабатываемого сигнала. В силу этого медианный фильтр относится к числу нелинейных фильтров, заменяющих медианным значением аномальные точки и выбросы независимо от их амплитудных значений, и является устойчивым по определению, способным аннулировать даже бесконечно большие отсчеты.
Достоинством медианных фильтров является простота структуры, позволяющая легко реализовать фильтр как аппаратными, так и программными средствами. Медианный фильтр не применяется для ступенчатых и пилообразных функций, однако он хорошо подавляет одиночные импульсные помехи (случайные шумовые выбросы отсчетов и промахи).
Медианные фильтры имеют следующие недостатки:
− медианная фильтрация – метод нелинейной обработки сигналов, так как медиана суммы двух произвольных последовательностей не равна сумме их медиан – это усложняет математический анализ их характеристик; нельзя разграничить влияние этих фильтров на сигнал и шум, что для линейных фильтров делается очень просто;
− фильтр вызывает уплощение вершин треугольной функции;
− подавление гауссовского шума менее эффективно, чем у линейных фильтров;
− двумерная обработка приводит к более существенному ослаблению сигнала.
Авторами были промоделированы различные реализации медианных фильтров, где в качестве верхней границы окна брался текущий показатель измерения загруженности (рис. 2), таким образом,  , где qn,
, где qn,  – измеренное и предсказываемое значения параметра в n-й и (n+1)-й моменты времени; T – ширина окна. Ошибки прогнозирования для медианного фильтра в зависимости от T представлены в таблице 4.
– измеренное и предсказываемое значения параметра в n-й и (n+1)-й моменты времени; T – ширина окна. Ошибки прогнозирования для медианного фильтра в зависимости от T представлены в таблице 4.
Таблица 4
Ошибки прогнозирования для медианного фильтра
Table 4
Mispredictions for a median filter
|
Параметр T
|
Средняя ошибка прогнозирования
|
Дисперсия ошибки
|
Максимальная ошибка прогнозирования
|
|
3
|
0,072
|
5,2´10-3
|
0,5
|
|
5
|
0,074
|
5,4´10-3
|
0,53
|
|
10
|
0,078
|
6,1´10-3
|
0,535
|
|
15
|
0,084
|
7´10-3
|
0,56
|
|
20
|
0,089
|
7,8´10-3
|
0,575
|
|
25
|
0,093
|
8,6´10-3
|
0,58
|
|
30
|
0,095
|
9´10-3
|
0,58
|
|
35
|
0,098
|
9,5´10-3
|
0,58
|
|
40
|
0,105
|
0,011
|
0,58
|
|
45
|
0,105
|
0,011
|
0,58
|
|
50
|
0,11
|
0,012
|
0,58
|
Сравнение методов
В таблице 5 приведены наилучшие значения средней, максимальной и дисперсии ошибки прогнозирования для каждого из методов.
Таблица 5
Наилучшие значения ошибки прогнозирования
Table 5
The best values of misprediction
|
Метод
|
Средняя ошибка прогнозирования
|
Дисперсия ошибки
|
Максимальная ошибка прогнозирования
|
|
Экспоненциальное сглаживание (x=0,5)
|
0,08
|
6,3´10-3
|
0,45
|
|
Экстраполятор с равномерным окном (T =5)
|
0,092
|
8,5´10-3
|
0,472
|
|
Экстраполятор с подбором ширины окна (s=4, T=10, 30, 40)
|
0,092
|
8,5´10-3
|
0,464
|
|
Медианный фильтр (T=3)
|
0,072
|
5,2´10-3
|
0,5
|
Из приведенных данных видно, что экспоненциальное сглаживание, экстраполятор с равномерным окном и экстраполятор с подбором ширины окна и весовых коэффициентов дают близкие результаты. Медианный фильтр в среднем дает улучшение результатов на 25–35 % по сравнению с предыдущими методами.
Средняя дисперсия ошибки при прогнозировании для данной реализации путем выбора константы по предыдущему значению составила 0,101.
Значения средней ошибки прогнозирования загруженности процессора путем выбора единственной константы для всей реализации (например, предполагаем, что процесс всегда принимает значение 0,3) следующие:
|
Константа
|
Ошибка
|
|
0,1
|
0,263
|
|
0,2
|
0,165
|
|
0,3
|
0,118
|
|
0,4
|
0,147
|
|
0,5
|
0,203
|
Очевидно, что в зависимости от выбора конкретной константы средняя ошибка прогнозирования существенно изменяется. Значит, не зная поведения процесса, нельзя выбрать такую константу (отсутствие прогнозирования), которая всегда давала бы приемлемые результаты. Поэтому необходимо постоянно прогнозировать загруженность компонентов КС для достижения успешного и эффективного управления процессами в КС.
В заключение отметим, что исследования точности прогнозирования загруженности процессора с применением рассмотренных фильтров были выполнены на достаточно представительном наборе приложений. Полученные данные позволяют сделать вывод, что наиболее точным методом прогнозирования загруженности процессора является медианный фильтр. При этом преимущество медианных фильтров особенно заметно для процессов с высокой амплитудой колебания параметра загруженности. На так называемых гладких графиках процессов этот эффект не столь очевиден.
Помимо всего, медианный фильтр достаточно просто реализуется на практике и требует немного времени на определение прогноза загруженности. Результаты выполненных исследований составили основу для построения эффективных алгоритмов управления параллельными процессами на кластерах и распределенных компьютерных системах.
Литература
1. Проект по составлению рейтинга и описанию 500 самых мощных вычислительных систем мира. URL: http://www.top500. org (дата обращения: 05.04.2015).
2. Кутепов В.П., Фальк В.Н. Формы, языки представления, критерии и параметры сложности параллелизма // Программные продукты и системы. 2010. № 3. С. 16–26.
3. Кутепов В.П. О параллелизме с разных сторон // Параллельные вычисления и проблемы управления: матер. 5-й Междунар. конф. М.: Изд-во ИПУ РАН, 2010.
4. Тауб С., Шафри Х. Улучшенная поддержка распараллеливания в следующей версии Visual Studio // Журнал для разработчиков MSDN Magazine. 2008. № 11 (83).
5. Кутепов В.П. Интеллектуальное управление процессами и загруженностью в вычислительных системах // Изв. РАН. ТиСУ. 2007. № 5.
6. Kutepov V.P. Scheduling parallel processes and load balancing in large-scale computing systems. Proc. Intern. Symp. on Distributed Computing and Application for Business? Engineering and Science. China, 2007, vol. 1.
7. Кутепов В.П., Шамаль П.Н. Реализация языка функционального параллельного программирования FPTL на многоядерных компьютерах // Изв. РАН. ТиСУ. 2014. № 3.
8. Кутепов В.П., Маланин В.Н., Панков Н.А. Граф-схемное потоковое параллельное программирование: язык, процессная модель, реализация на компьютерных системах // Изв. РАН. ТиСУ. 2012. № 1.
9. Айфичер Э., Джервис Б. Цифровая обработка сигналов. Практический подход // М.: Вильямс, 2004.

 на момент будущего представляется как константа, равная полученному сглаженному значению
на момент будущего представляется как константа, равная полученному сглаженному значению  в текущий момент времени:
в текущий момент времени: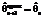 . (1)
. (1)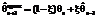 , где qn – измеренное значение параметра в n-й момент времени;
, где qn – измеренное значение параметра в n-й момент времени;  , а максимальная ошибка прогнозирования по формуле
, а максимальная ошибка прогнозирования по формуле 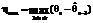 .
. , где qn-k – измеренное значение параметра в (n–k)-й момент времени, k≥1;
, где qn-k – измеренное значение параметра в (n–k)-й момент времени, k≥1;  где qn-i – измеренное значение параметра в (n–i)-й момент времени;
где qn-i – измеренное значение параметра в (n–i)-й момент времени;  , где
, где 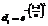 .
.
 , где qn,
, где qn, 